10.1: Filling the Plate
About how many cheese puffs can fit on the plate in a single layer? Be prepared to explain your reasoning.

Let’s contrast circumference and area.
About how many cheese puffs can fit on the plate in a single layer? Be prepared to explain your reasoning.

Your teacher will give you cards with questions about circles.
In the previous activity you estimated the answer to a question about circles.
Create a visual display that includes:
Here are two students’ answers for each question. Do you agree with either of them? Explain or show your reasoning.
How many feet are traveled by a person riding once around the merry-go-round?
How much room is there to spread frosting on the cookie?

How far does the unicycle move when the wheel makes 5 full rotations?

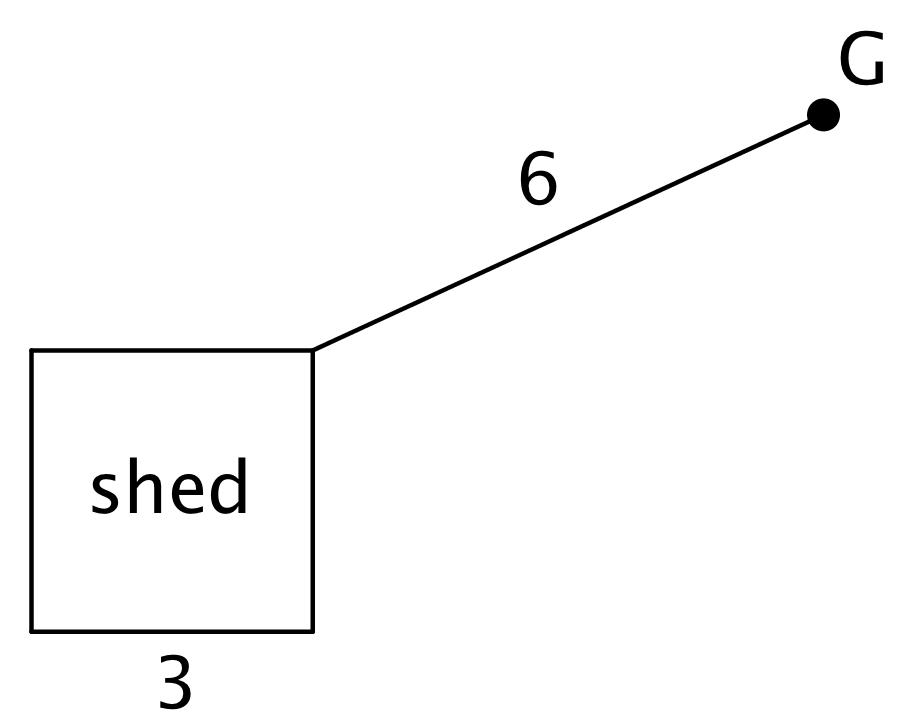
A goat (point G) is tied with a 6-foot rope to the corner of a shed. The floor of the shed is a square whose sides are each 3 feet long. The shed is closed and the goat can't go inside. The space all around the shed is flat, grassy, and the goat can't reach any other structures or objects. What is the area over which the goat can roam?
Sometimes we need to find the circumference of a circle, and sometimes we need to find the area. Here are some examples of quantities related to the circumference of a circle:
Here are some examples of quantities related to the area of a circle:
In both cases, the radius (or diameter) of the circle is all that is needed to make the calculation. The circumference of a circle with radius r is 2\pi r while its area is \pi r^2. The circumference is measured in linear units (such as cm, in, km) while the area is measured in square units (such as cm2, in2, km2).