4.1: True or False: Length Relationships
Here are some line segments.

Decide if each of these equations is true or false. Be prepared to explain your reasoning.
$CD+BC=BD$
$AB+BD=CD+AD$
$AC-AB=AB$
$BD-CD=AC-AB$
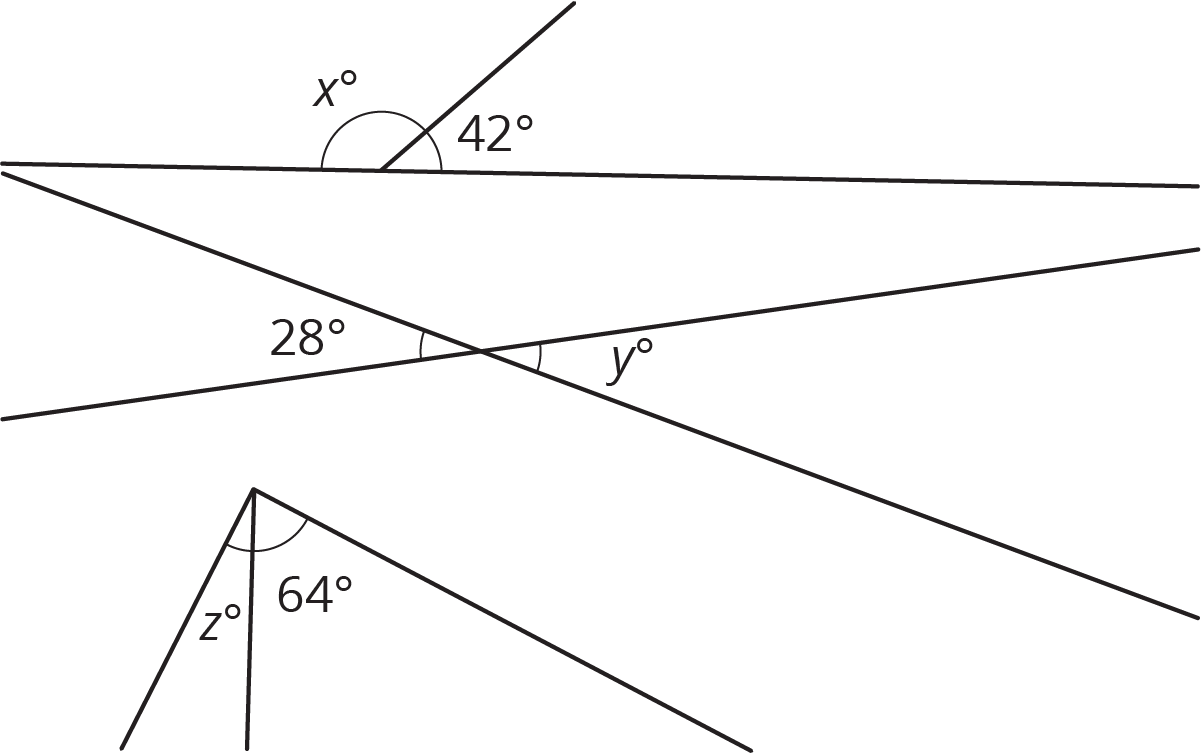
Let’s figure out some missing angles.
Here are some line segments.

Decide if each of these equations is true or false. Be prepared to explain your reasoning.
$CD+BC=BD$
$AB+BD=CD+AD$
$AC-AB=AB$
$BD-CD=AC-AB$
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.
If your teacher gives you the problem card:
If your teacher gives you the data card:
Match each figure to an equation that represents what is seen in the figure. For each match, explain how you know they are a match.
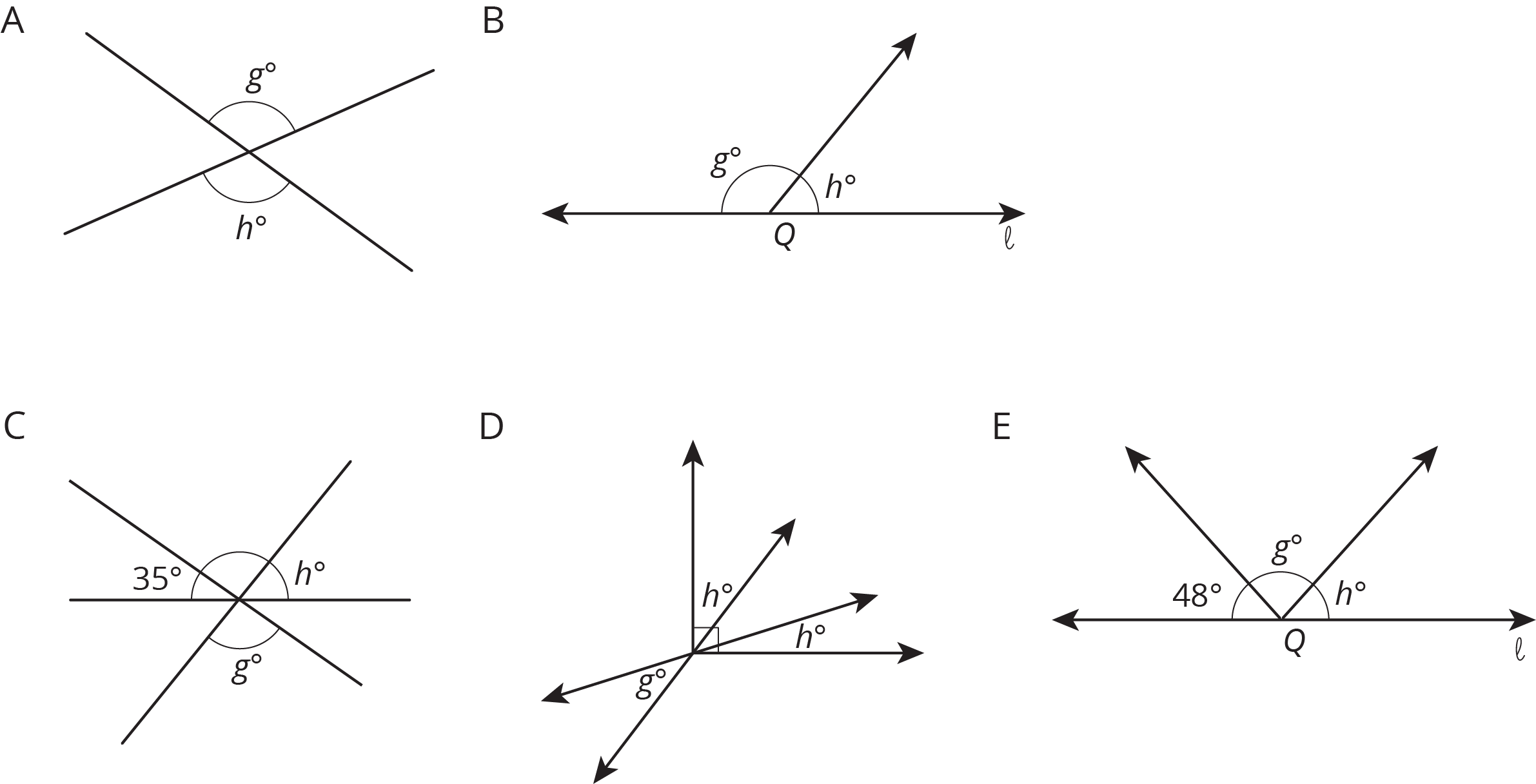
We can write equations that represent relationships between angles.