Lesson 6: Increasing and Decreasing

Let’s use percentages to describe increases and decreases.

6.1: Improving Their Game

Here are the scores from 3 different sports teams from their last 2 games.

sports team total points in game 1 total points in game 2
football team 22 30
basketball team 100 108
baseball team 4 12
  1. What do you notice about the teams’ scores? What do you wonder?
  2. Which team improved the most? Explain your reasoning.

6.2: More Cereal and a Discounted Shirt

  1. ​​A cereal box says that now it contains 20% more. Originally, it came with 18.5 ounces of cereal. How much cereal does the box come with now?

     

    Picture of a cereal box with the label "20% more free" on the box.

  2. The price of a shirt is \$18.50, but you have a coupon that lowers the price by 20%. What is the price of the shirt after using the coupon?

     

6.3: Using Tape Diagrams

  1. Match each situation to a diagram. Be prepared to explain your reasoning.

    1. Compared with last year’s strawberry harvest, this year’s strawberry harvest is a 25% increase.
    2. This year’s blueberry harvest is 75% of last year’s.
    3. Compared with last year, this year’s peach harvest decreased 25%.
    4. This year’s plum harvest is 125% of last year’s plum harvest.

  2. Draw a diagram to represent these situations.

    1. The number of ducks living at the pond increased by 40%.
    2. The number of mosquitoes decreased by 80%.

6.4: Agree or Disagree: Percentages

Do you agree or disagree with each statement? Explain your reasoning.

  1. Employee A gets a pay raise of 50%. Employee B gets a pay raise of 45%. So Employee A gets the bigger pay raise.
  2. Shirts are on sale for 20% off. You buy two of them. As you pay, the cashier says, “20% off of each shirt means 40% off of the total price.”

Summary

Imagine that it takes Andre $\frac34$ more than the time it takes Jada to get to school. Then we know that Andre’s time is $1\frac34$ or 1.75 times Jada’s time. We can also describe this in terms of percentages:

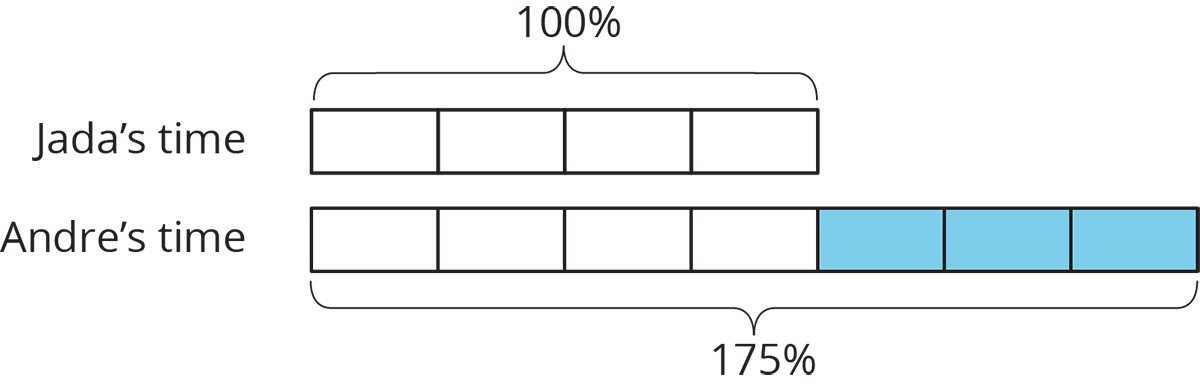
We say that Andre’s time is 75% more than Jada’s time. We can also see that Andre’s time is 175% of Jada’s time. In general, the terms percent increase and percent decrease describe an increase or decrease in a quantity as a percentage of the starting amount.

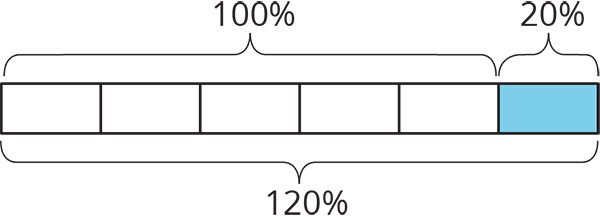
For example, if there were 500 grams of cereal in the original package, then “20% more” means that 20% of 500 grams has been added to the initial amount, $500+(0.2)\boldcdot 500=600$, so there are 600 grams of cereal in the new package.

Picture of a cereal box with the label "20% more free" on the box.

We can see that the new amount is 120% of the initial amount because

$$500+(0.2)\boldcdot 500 = (1 + 0.2)500$$

Practice Problems ▶

Glossary

percentage increase

percentage increase

Given an initial amount, and a final amount which is larger than the initial amount, the percentage increase is the difference (final amount minus initial amount) expressed as a percentage of the initial amount.  

percentage decrease

percentage decrease

Given an initial amount, and a final amount which is smaller than the initial amount, the percentage decrease is the difference (initial amount minus final amount) expressed as a percentage of the initial amount.