7.1: Estimating Areas
Your teacher will show you some figures. Decide which figure has the largest area. Be prepared to explain your reasoning.
Lesson 7: Exploring the Area of a Circle
Let’s investigate the areas of circles.
7.2: Estimating Areas of Circles
Your teacher will assign your group two circles of different sizes.
- Set the diameter of your assigned circle and use the applet to help estimate the area of the circle.
Note: to create a polygon, select the Polygon tool, and click on each vertex. End by clicking the first vertex again. For example, to draw triangle ABC, click on A-B-C-A.
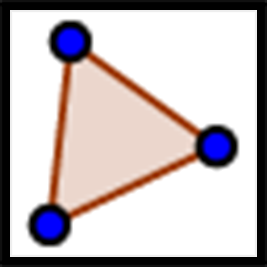
- Record the diameter in column D and the corresponding area in column A for your circles and others from your classmates.
| trig | stats | misc |
| trig | inverse | hyperb |
| sin | sin | sinh |
| cos | cos | cosh |
| tan | tan | tanh |
| csc | csc | csch |
| sec | sec | sech |
| cot | cot | coth |
x
y
a
a
a
A B C
funcs
q
w
e
r
t
y
u
i
o
p
a
s
d
f
g
h
j
k
l
z
x
c
v
b
n
m
1 2 3
a
( )
{ }
[ ]
Q
W
E
R
T
Y
U
I
O
P
A
S
D
F
G
H
J
K
L
Z
X
C
V
B
N
M
1 2 3
a
( )
{ }
[ ]
a
b
c
d
e
f
g
h
i
j
k
l
m
n
o
p
q
r
s
t
u
v
w
x
y
z
1 2 3
a
( )
{ }
[ ]
Drop Image Here
D
A
powered by
powered by
-
In a previous lesson, you graphed the relationship between the diameter and circumference of a circle. How is this graph the same? How is it different?
- How many circles of radius 1 unit can you fit inside a circle of radius 2 units so that they do not overlap?
- How many circles of radius 1 unit can you fit inside a circle of radius 3 units so that they do not overlap?
- How many circles of radius 1 unit can you fit inside a circle of radius 4 units so that they do not overlap?
If you get stuck, consider using coins or other circular objects.
7.3: Covering a Circle
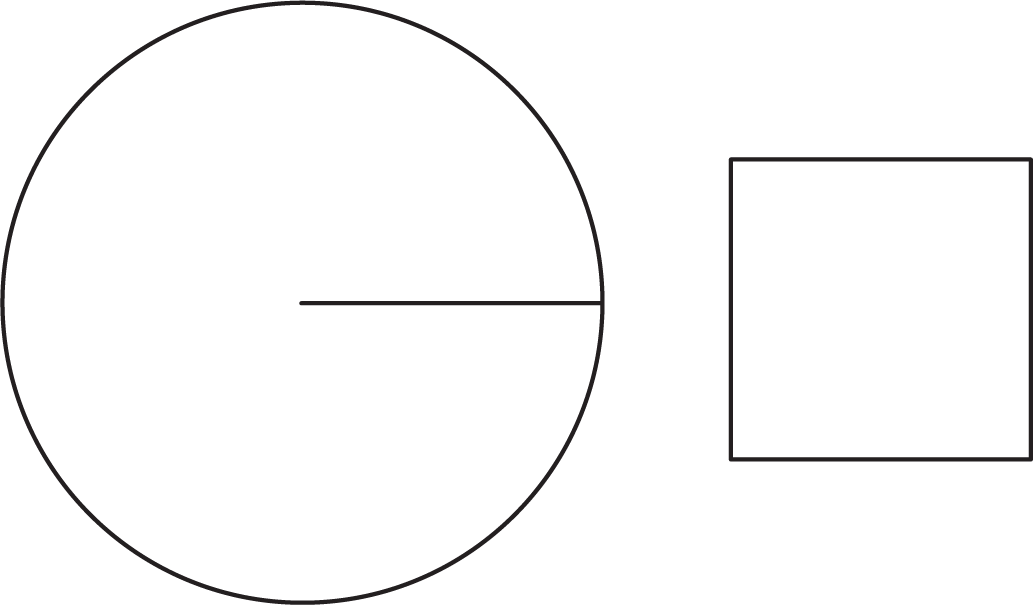
Here is a square whose side length is the same as the radius of the circle.
How many of the squares do you think it would take to cover the circle exactly?
Summary
The circumference C of a circle is proportional to the diameter d, and we can write this relationship as C = \pi d. The circumference is also proportional to the radius of the circle, and the constant of proportionality is 2 \boldcdot \pi because the diameter is twice as long as the radius. However, the area of a circle is not proportional to the diameter (or the radius).
The area of a circle with radius r is a little more than 3 times the area of a square with side r so the area of a circle of radius r is approximately 3r^2. We saw earlier that the circumference of a circle of radius r is 2\pi r. If we write C for the circumference of a circle, this proportional relationship can be written C = 2\pi r.
The area A of a circle with radius r is approximately 3r^2. Unlike the circumference, the area is not proportional to the radius because 3r^2 cannot be written in the form kr for a number k. We will investigate and refine the relationship between the area and the radius of a circle in future lessons.
Practice Problems ▶
Glossary
-
area of a circle
area of a circle
The area of a circle whose radius is r units is \pi r^2 square units.