3.1: Which Is Greater?
Clare wonders if the height of the toilet paper tube or the distance around the tube is greater. What information would she need in order to solve the problem? How could she find this out?

Let’s explore the circumference of circles.
Clare wonders if the height of the toilet paper tube or the distance around the tube is greater. What information would she need in order to solve the problem? How could she find this out?

Coins, cookies, and drinking glasses are some examples of common circular objects.
Explore the applet to find the diameter and the circumference of three circular objects to the nearest tenth of a unit. Record your measurements in the table.
Plot the diameter and circumference values from the table on the coordinate plane. What do you notice?
Suppose you had another circular object with a diameter that is half as long as the diameter of your largest circle. What would its circumference be?
Here are five circles. One measurement for each circle is given in the table.
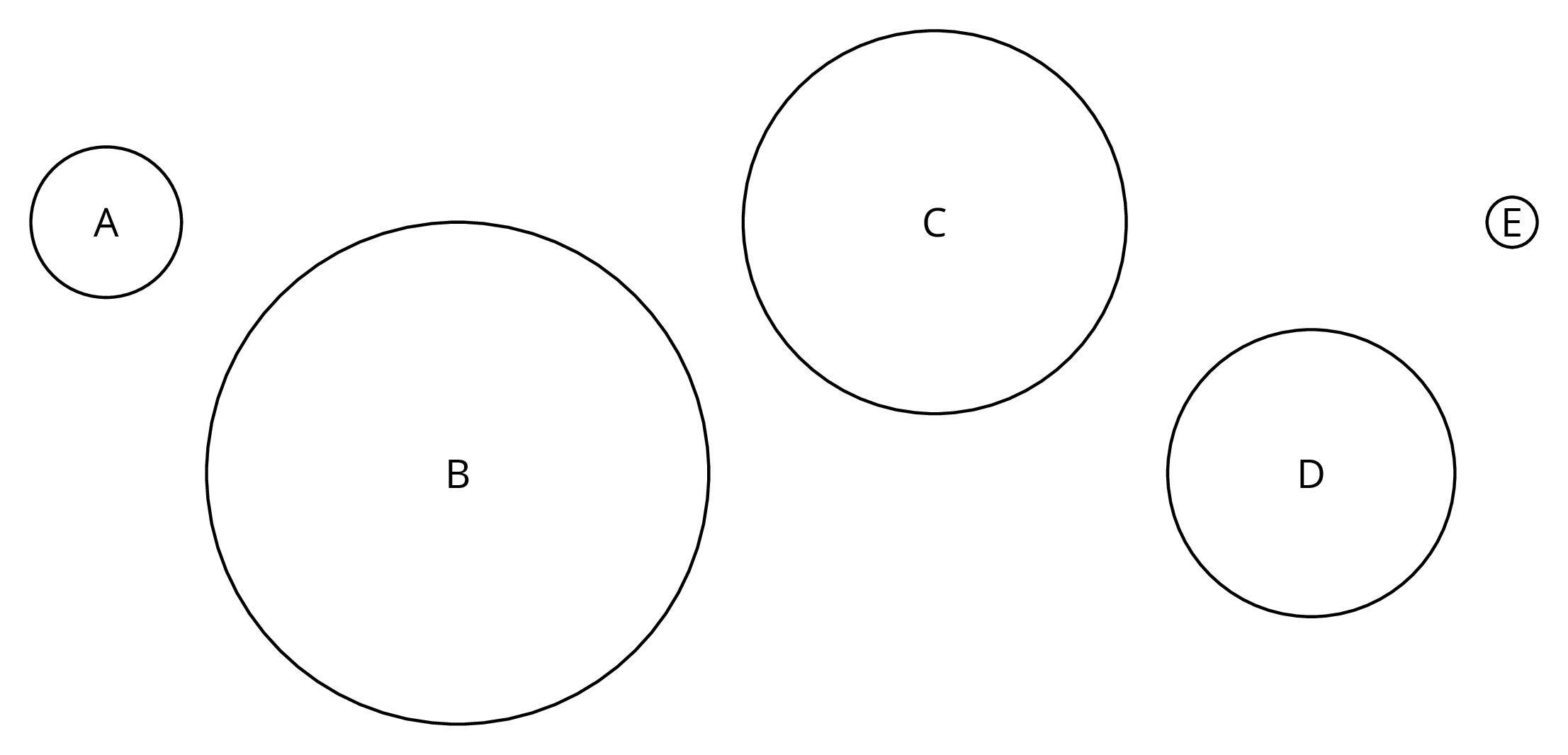
Use the constant of proportionality estimated in the previous activity to complete the table.
| diameter (cm) | circumference (cm) | |
|---|---|---|
| circle A | 3 | |
| circle B | 10 | |
| circle C | 24 | |
| circle D | 18 | |
| circle E | 1 |
The circumference of the Earth is approximately 40,000 km. If you made a circle of wire around the globe, that is only 10 meters (0.01 km) longer than the circumference of the globe, could a flea, a mouse, or even a person creep under it?
There is a proportional relationship between the diameter and circumference of any circle. That means that if we write C for circumference and d for diameter, we know that C=kd, where k is the constant of proportionality.
The exact value for the constant of proportionality is called \boldsymbol\pi. Some frequently used approximations for \pi are \frac{22} 7, 3.14, and 3.14159, but none of these is exactly \pi.

We can use this to estimate the circumference if we know the diameter, and vice versa. For example, using 3.1 as an approximation for \pi, if a circle has a diameter of 4 cm, then the circumference is about (3.1)\boldcdot 4 = 12.4 or 12.4 cm.
The relationship between the circumference and the diameter can be written as
C = \pi d
The Greek letter \pi (pronounced "pie") stands for the number that is the constant of proportionality between the circumference of a circle and its diameter. If d is the diameter and C is the circumference, then C = \pi d.