11.1: Coordinates and Lengths in the Coordinate Plane
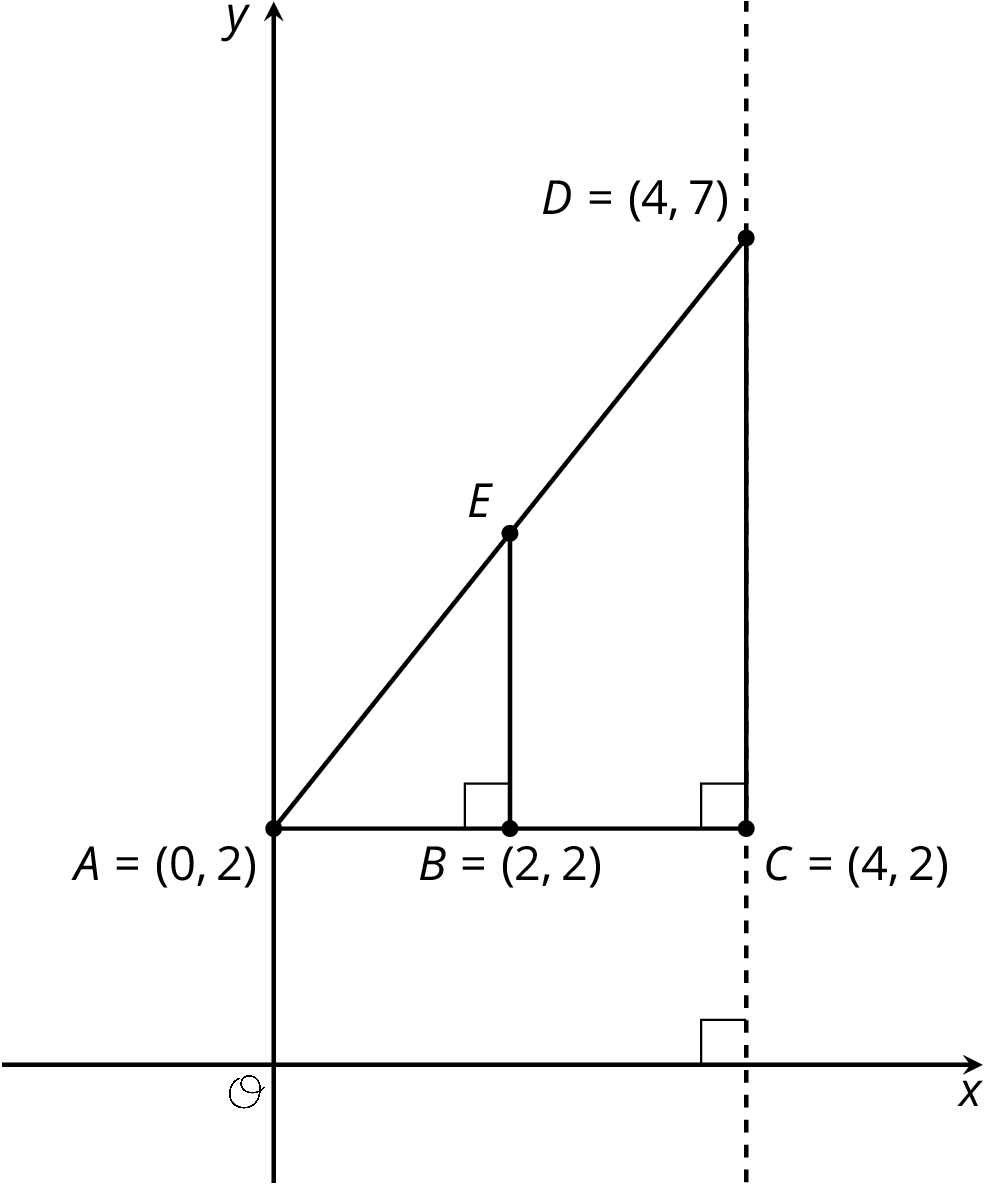
Find each of the following and explain your reasoning:
- The length of segment BE.
- The coordinates of E.
Let’s explore the relationship between points on a line and the slope of the line.

Find each of the following and explain your reasoning:
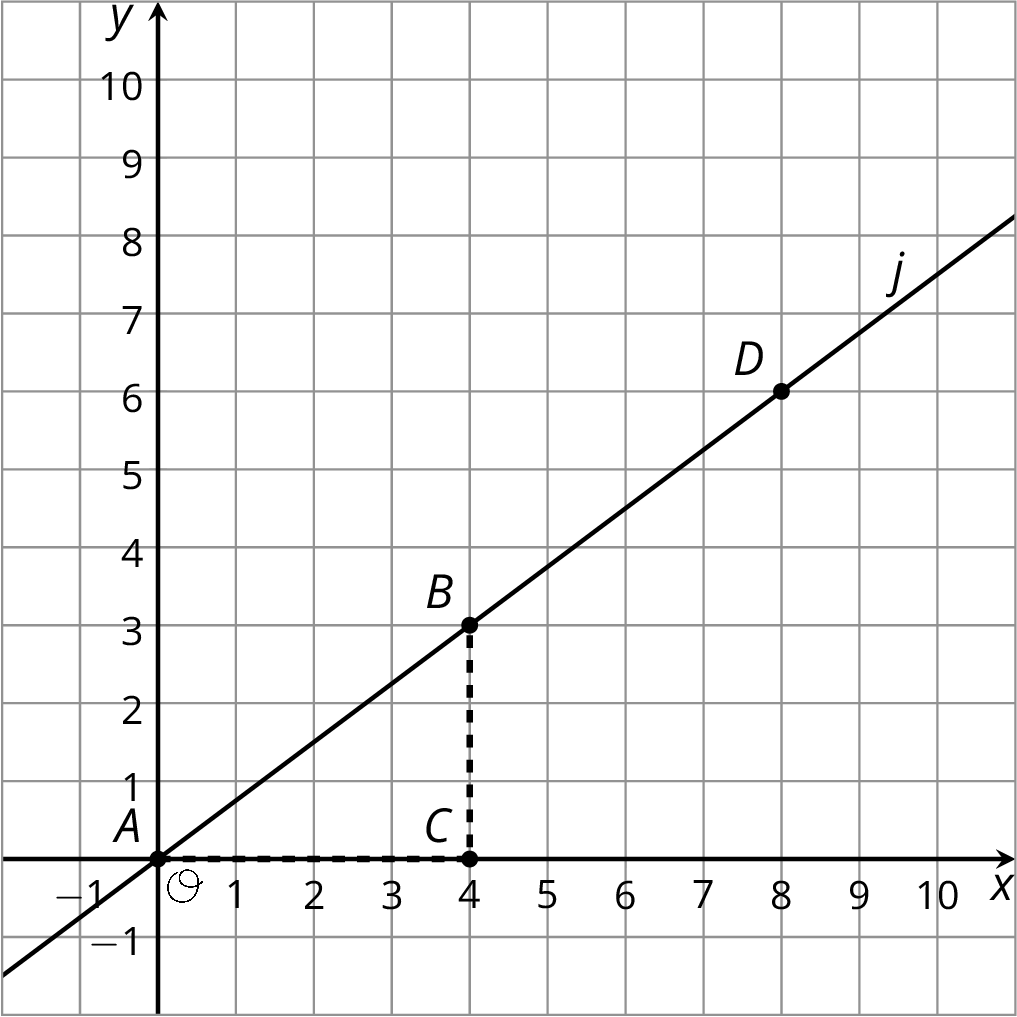
Line j is shown in the coordinate plane.
Is point (20,15) on line j? Explain how you know.
Is point (100,75) on line j? Explain how you know.
Is point (90,68) on line j? Explain how you know.
Suppose you know the x- and y-coordinates of a point. Write a rule that would allow you to test whether the point is on line j.
Here are two diagrams:
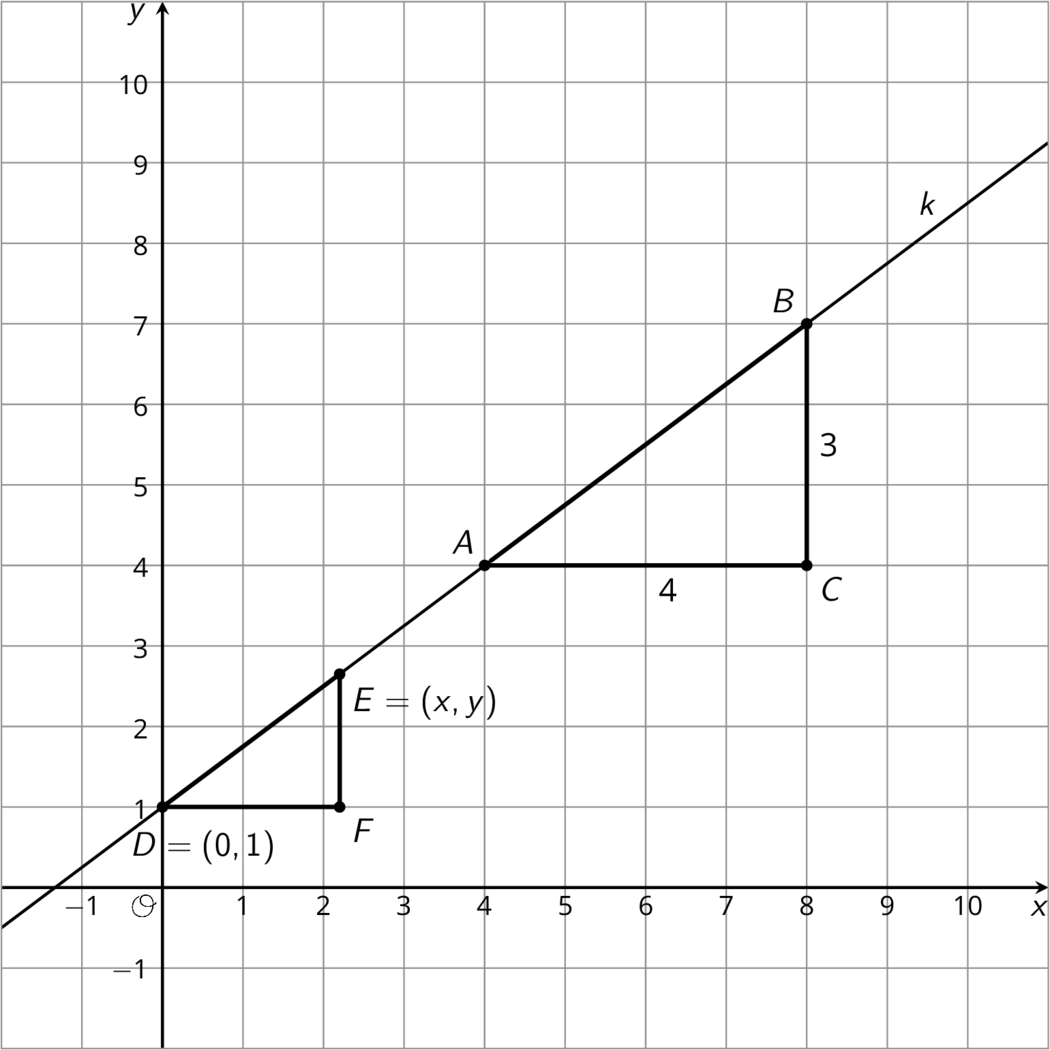

Here are the points A, C, and E on the same line. Triangles ABC and ADE are slope triangles for the line so we know they are similar triangles. Let’s use their similarity to better understand the relationship between x and y, which make up the coordinates of point E.
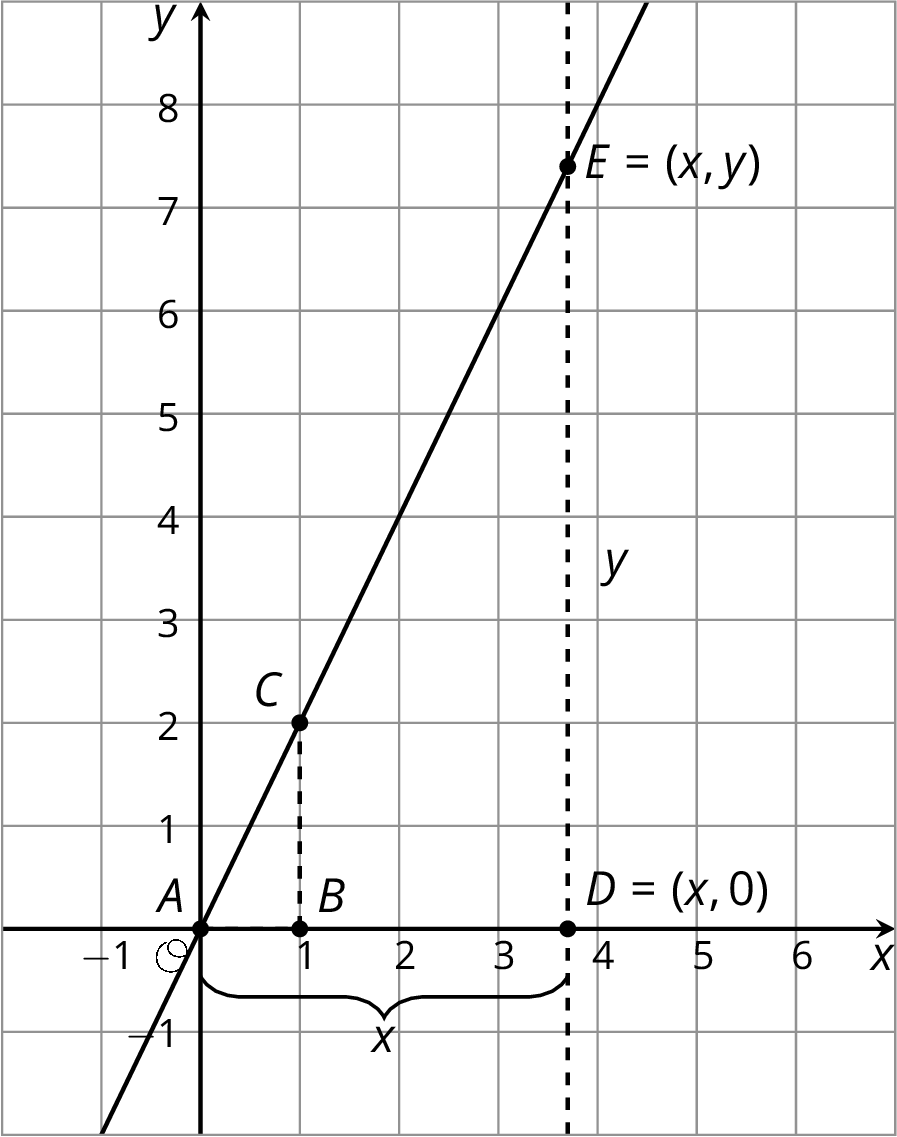
The slope for triangle ABC is \frac{2}{1} since the vertical side has length 2 and the horizontal side has length 1. The slope we find for triangle ADE is \frac{y}{x} because the vertical side has length y and the horizontal side has length x. These two slopes must be equal since they are from slope triangles for the same line, and so: \frac{2}{1} = \frac{y}{x}
Here are two different slope triangles. We can use the same reasoning to describe the relationship between x and y for this point E.
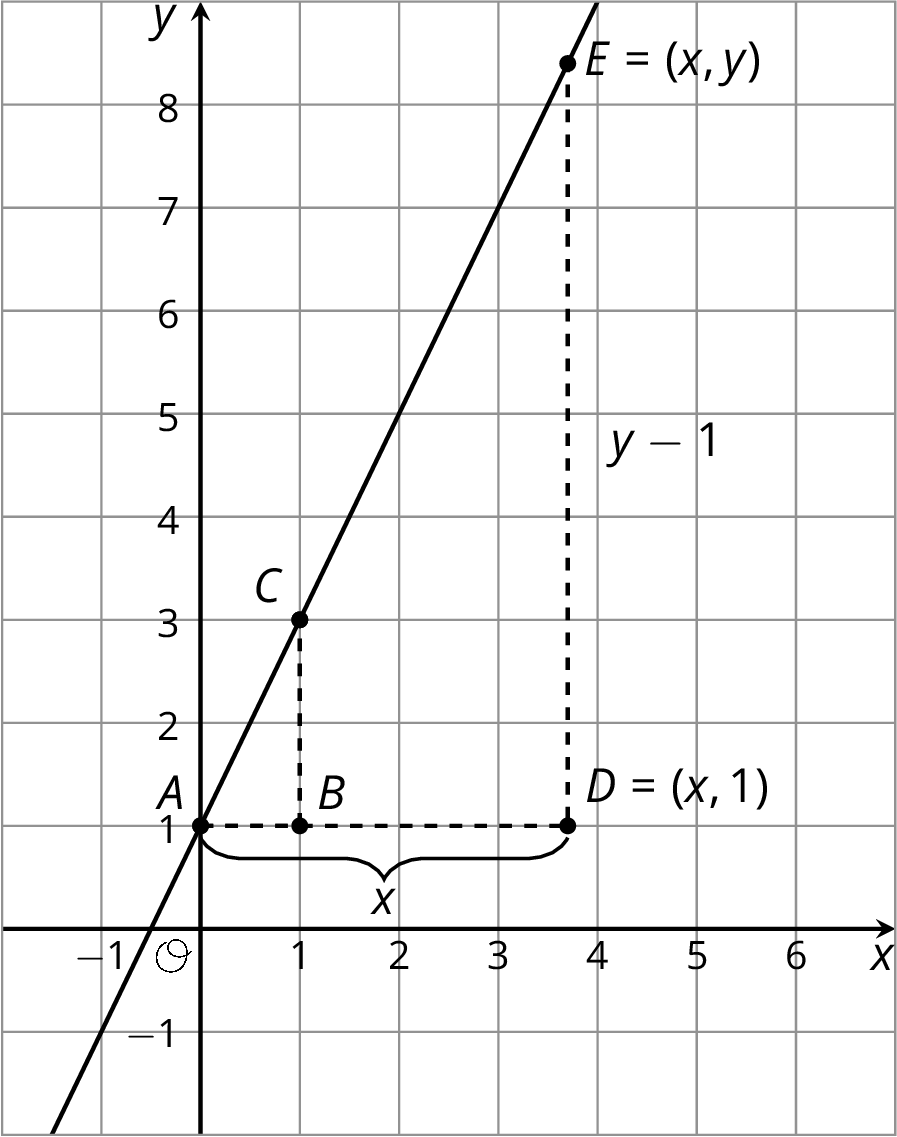
The slope for triangle ABC is \frac{2}{1} since the vertical side has length 2 and the horizontal side has length 1. For triangle ADE, the horizontal side has length x. The vertical side has length y-1 because the distance from (x,y) to the x-axis is y but the vertical side of the triangle stops 1 unit short of the x-axis. So the slope we find for triangle ADE is \frac{y-1}{x}. The slopes for the two slope triangles are equal, meaning: \frac{2}{1} = \frac{y-1}{x}
Since y-1 is twice x, another way to write this equation is y-1 = 2x. This equation is true for any point (x,y) on the line!