2.1: Notice and Wonder: Concentric Circles
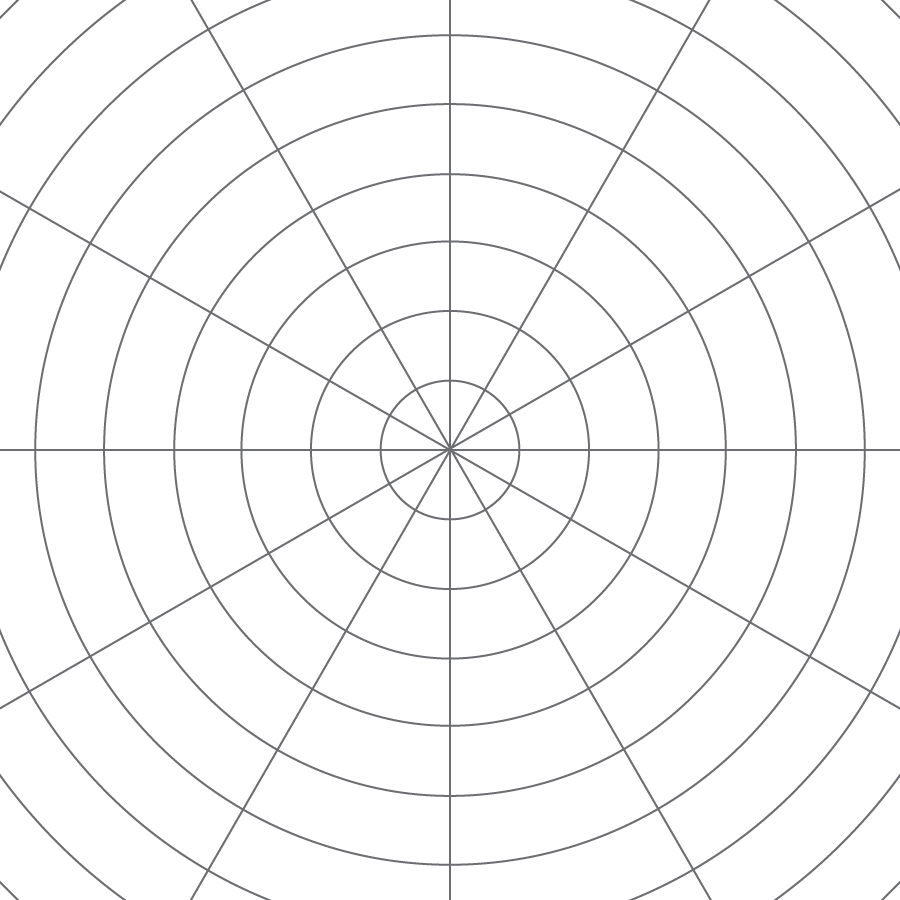
Let’s dilate figures on circular grids.

The larger circle d is a dilation of the smaller circle c. P is the center of dilation.
Draw four points on the smaller circle using the Point on Object tool. 
Draw the rays from P through each of those four points. Select the Ray tool, then point P, and then the second point. 
Mark the intersection points of the rays and circle d by selecting the Intersect tool and clicking on the point of intersection.
Complete the table. In the row labeled S, write the distance between P and the point on the smaller circle in grid units. In the row labeled L, write the distance between P and the corresponding point on the larger circle in grid units. Measure the distances between pairs of points by selecting the Distance tool, and then clicking on the two points. 
| A | B | C | D | |
|---|---|---|---|---|
| S | ||||
| L |
Dilate each vertex of polygon ABCD using P as the center of dilation and a scale factor of 2.
What are some things you notice about the new polygon?
Choose a few more points on the sides of the original polygon and transform them using the same dilation. What do you notice?
Dilate each vertex of polygon ABCD using P as the center of dilation and a scale factor of \frac{1}{2}.
What do you notice about this new polygon?
Suppose P is a point not on line segment \overline{WX}. Let \overline{YZ} be the dilation of line segment \overline{WX} using P as the center with scale factor 2. Experiment using a circular grid to make predictions about whether each of the following statements must be true, might be true, or must be false.
Dilate polygon EFGH using Q as the center of dilation and a scale factor of \frac13. The image of F is already shown on the diagram. (You may need to draw more rays from Q in order to find the images of other points.)
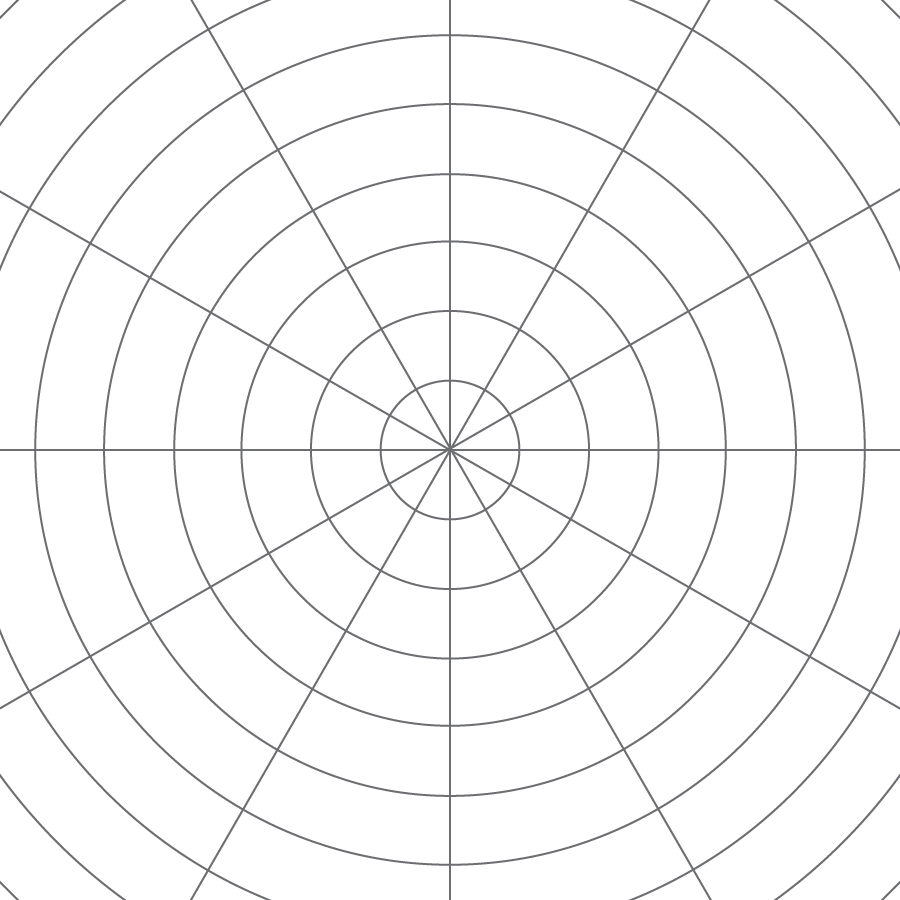
A circular grid like this one can be helpful for performing dilations.
The radius of the smallest circle is one unit, and the radius of each successive circle is one unit more than the previous one.
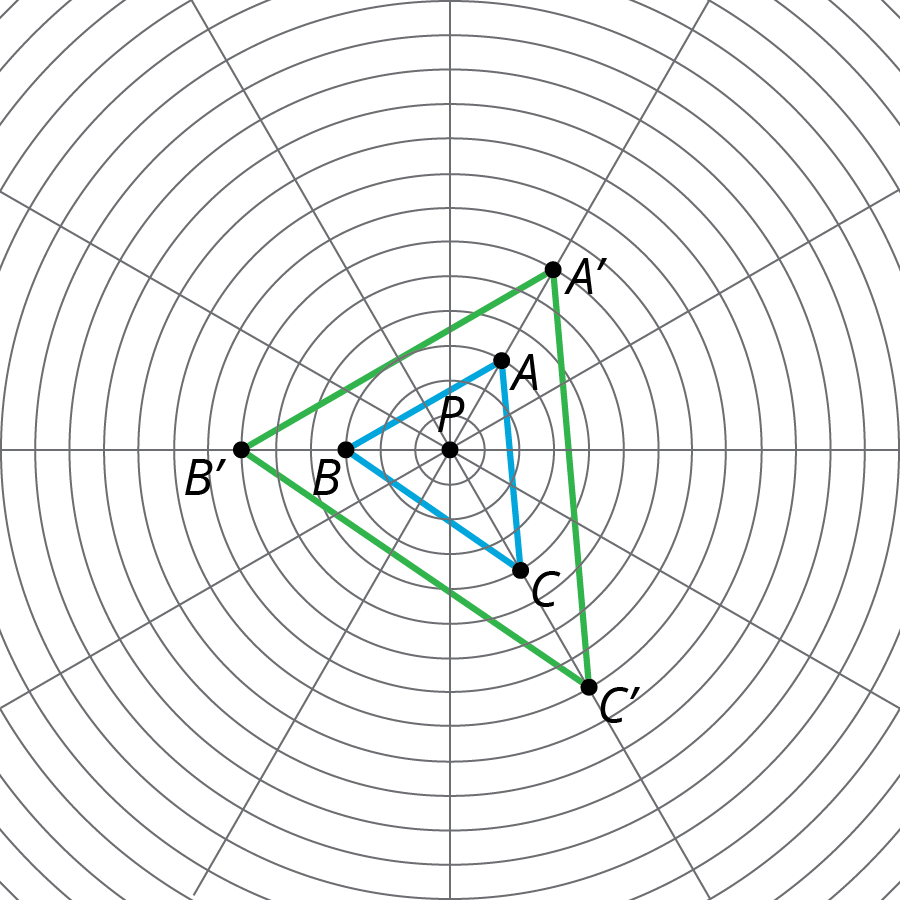
Since the circles on the grid are the same distance apart, segment PA' has twice the length of segment PA, and the same holds for the other points.
A dilation with center O and positive scale factor r takes a point P along the line OP to another point whose distance is r times further away from O than P is. If r < 1 then the new point is really closer to O, not further away.
The triangle DEF is a dilation of the triangle ABC with center O and with scale factor 3. So D is 3 times further away from O than A is, E is 3 times further away from O than B is, and F is 3 times further away from O than C is.
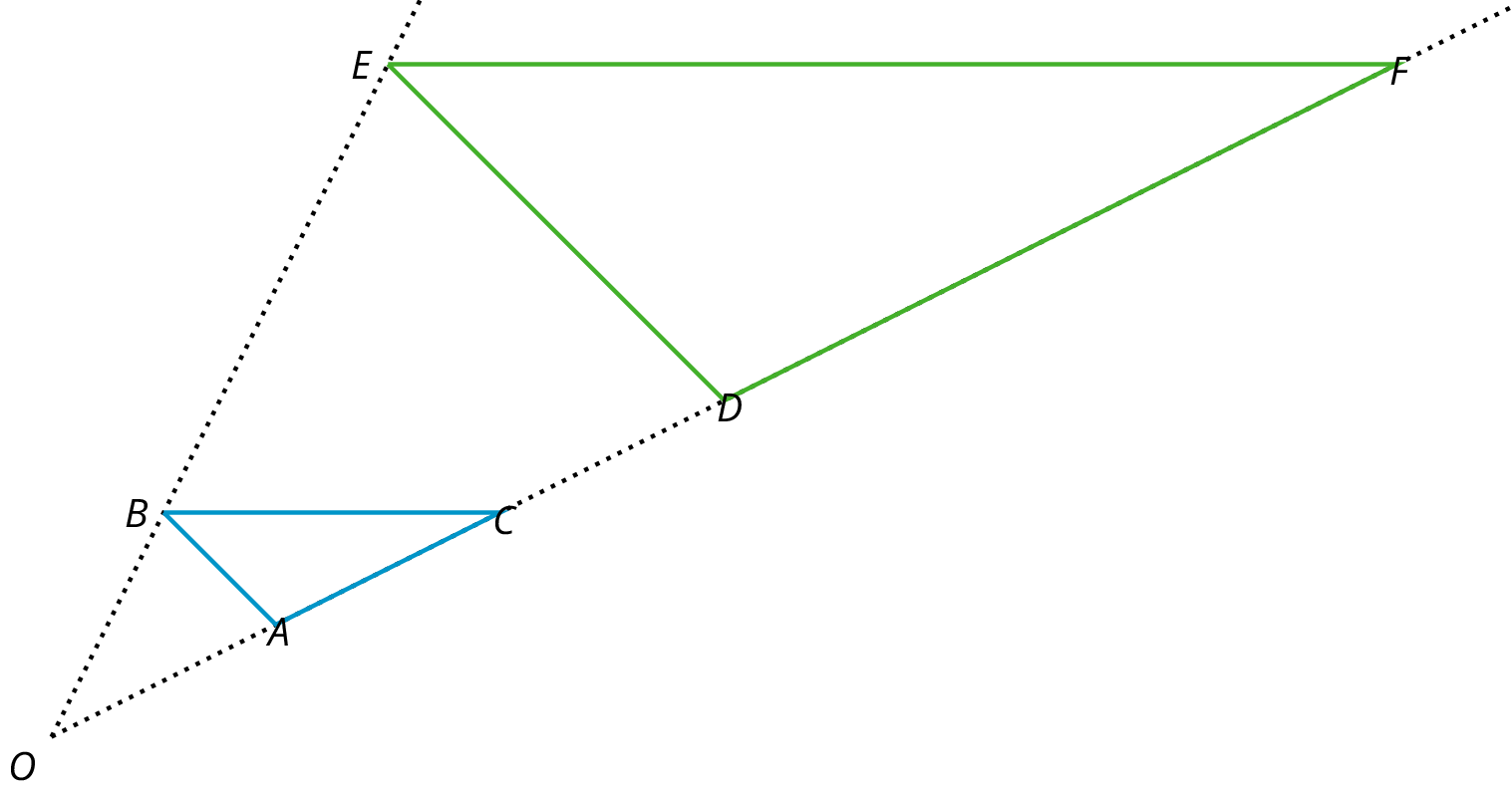
See dilation.