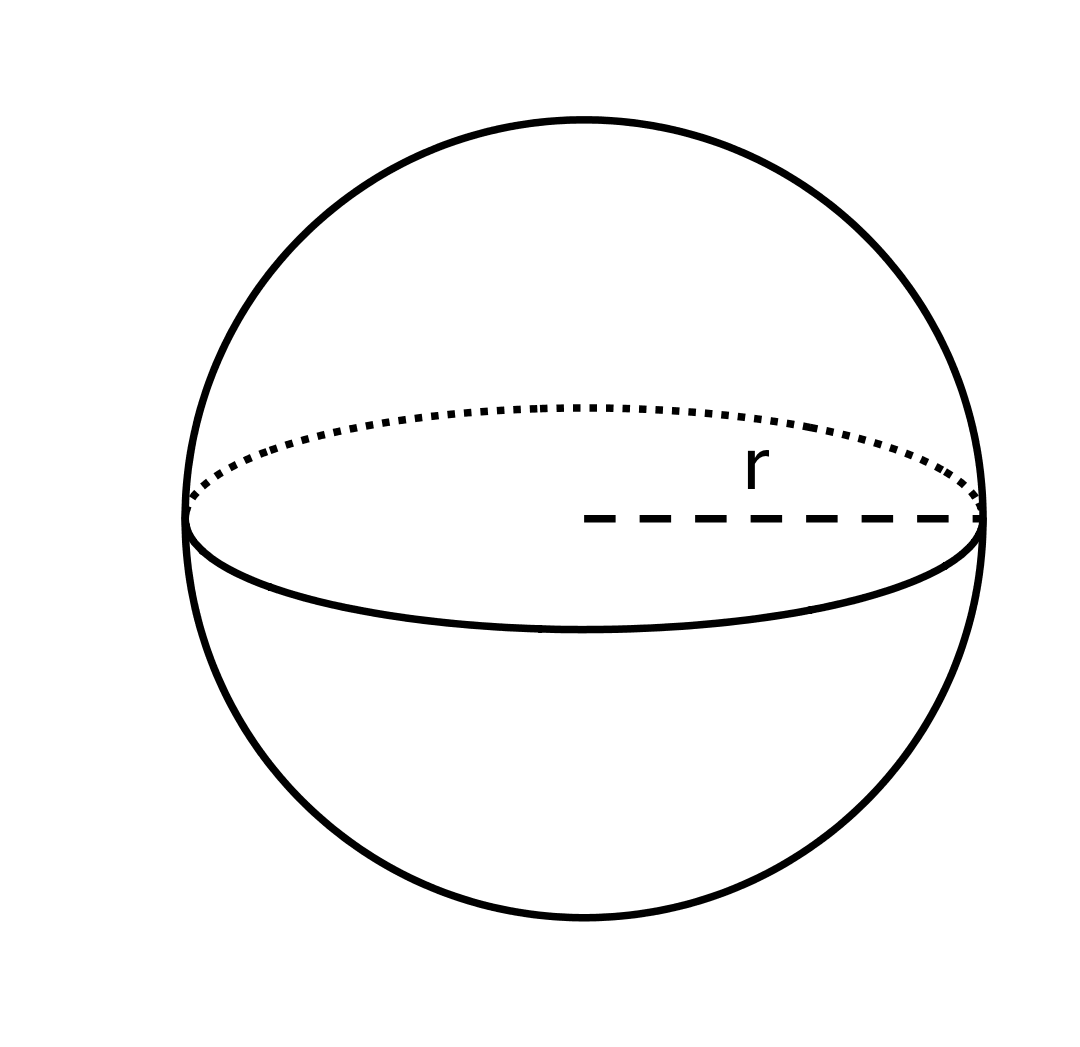
The formula
V=\frac43 \pi r^3
gives the volume of a sphere with radius r. We can use the formula to find the volume of a sphere with a known radius. For example, if the radius of a sphere is 6 units, then the volume would be
\frac{4}{3} \pi (6)^3 = 288\pi
or approximately 904 cubic units. We can also use the formula to find the radius of a sphere if we only know its volume. For example, if we know the volume of a sphere is 36 \pi cubic units but we don't know the radius, then this equation is true:
36\pi=\frac43\pi r^3
That means that r^3 = 27, so the radius r has to be 3 units in order for both sides of the equation to have the same value.
Many common objects, from water bottles to buildings to balloons, are similar in shape to rectangular prisms, cylinders, cones, and spheres—or even combinations of these shapes! Using the volume formulas for these shapes allows us to compare the volume of different types of objects, sometimes with surprising results.
For example, a cube-shaped box with side length 3 centimeters holds less than a sphere with radius 2 centimeters because the volume of the cube is 27 cubic centimeters (3^3 = 27), and the volume of the sphere is around 33.51 cubic centimeters (\frac43\pi \boldcdot 2^3 \approx 33.51).