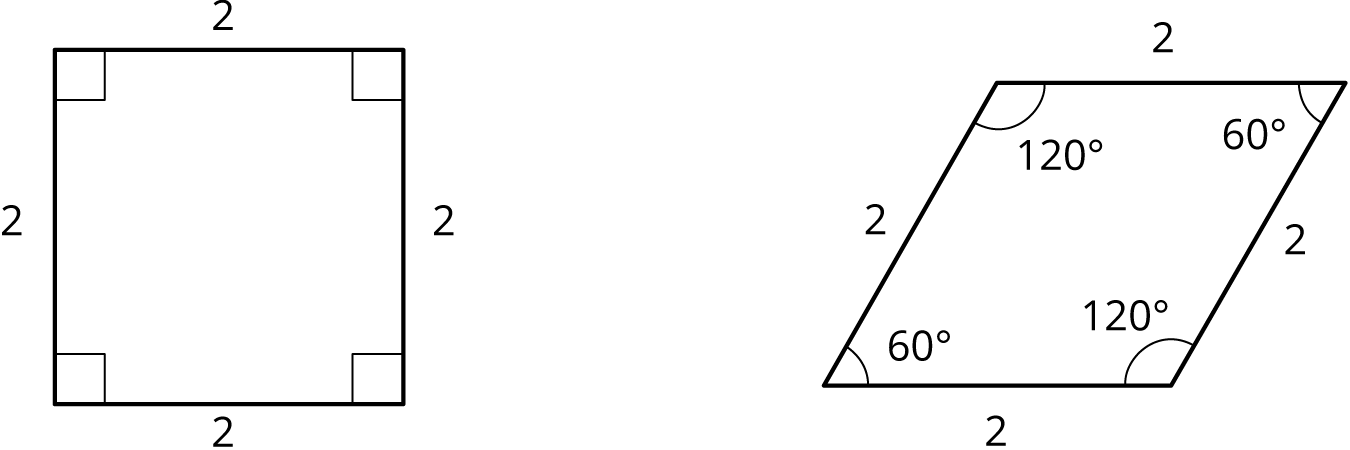When two polygons are similar:
- Every angle and side in one polygon has a corresponding part in the other polygon.
- All pairs of corresponding angles have the same measure.
- Corresponding sides are related by a single scale factor. Each side length in one figure is multiplied by the scale factor to get the corresponding side length in the other figure.
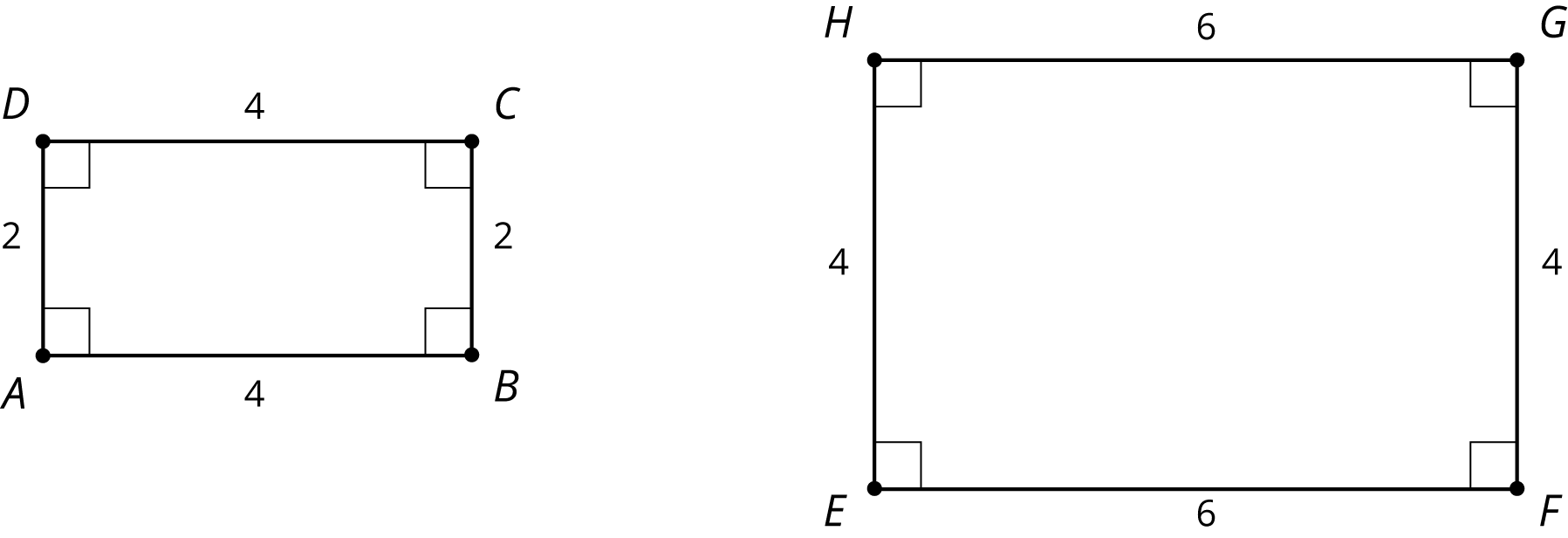
Consider the two rectangles shown here. Are they similar?
It looks like rectangles ABCD and EFGH could be similar, if you match the long edges and match the short edges. All the corresponding angles are congruent because they are all right angles. Calculating the scale factor between the sides is where we see that “looks like” isn’t enough to make them similar. To scale the long side AB to the long side EF, the scale factor must be \frac34, because 4 \boldcdot \frac34=3. But the scale factor to match AD to EH has to be \frac23, because 3\boldcdot \frac23=2. So, the rectangles are not similar because the scale factors for all the parts must be the same.
Here is an example that shows how sides can correspond (with a scale factor of 1), but the quadrilaterals are not similar because the angles don’t have the same measure: