Lesson 15: Infinite Decimal Expansions

Let’s think about infinite decimals.

15.1: Searching for Digits

The first 3 digits after the decimal for the decimal expansion of $\frac37$ have been calculated. Find the next 4 digits.

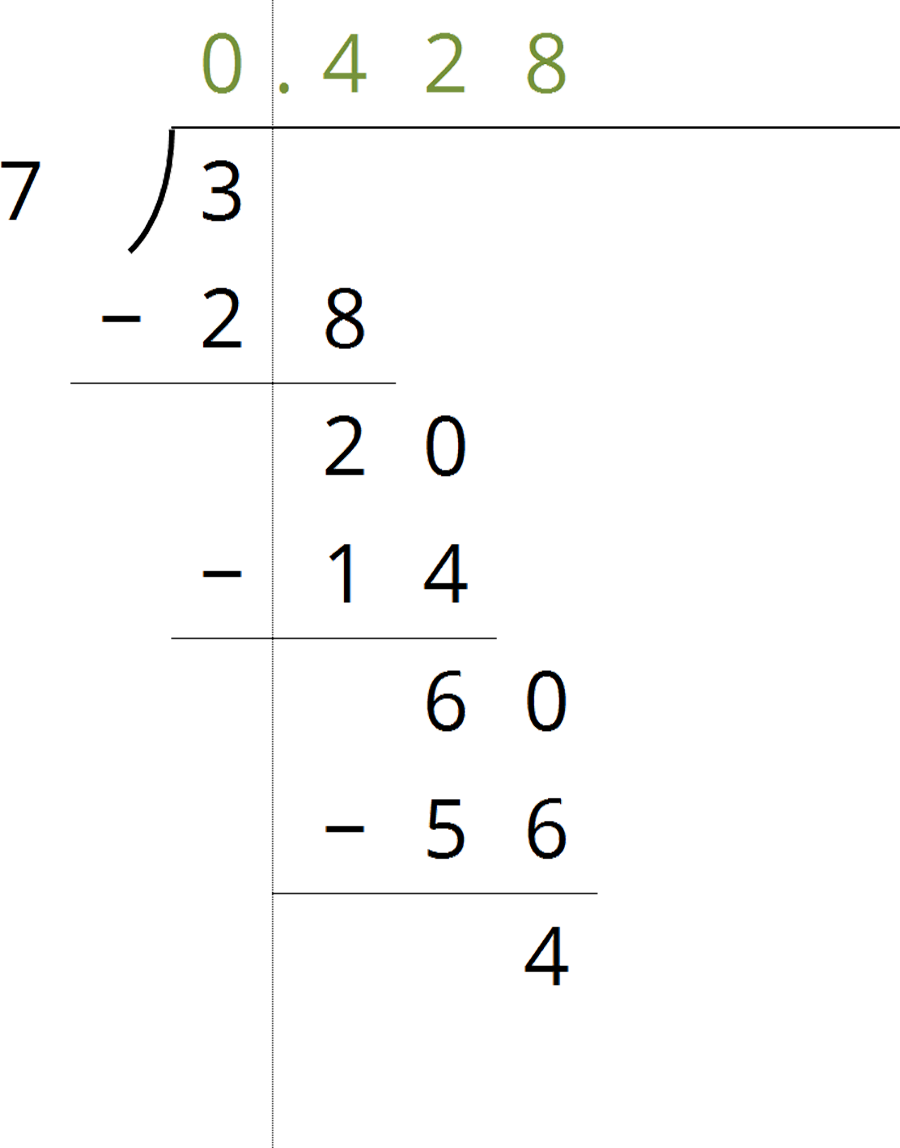
Long division calculations for decimal expansion, showing place value. The first line indicates the given place values of the quotient, 0 point 4 2 8. The second line indicates the division sentence 3 divided by 7; the number 7 is the left most number, followed by the long division symbol, and the number 3 inside; the 3 lines up vertically with the 0 above. On the third line reads as "minus twenty eight," with the 2 directly below the 3 from above. The fourth line reads "twenty," with the 2 directly below the 8 in 28. The fifth line reads "minus fourteen," with the 1 directly below the 2 in 20 and the 4 directly below the 0 in 20. The sixth line reads "sixty," with the 6 directly below the 4 in 14. The seventh line reads "minus fifty six" with the 5 directly below the 6 in 60, and the 6 directly below the 0 in 60. The eight line reads "4" with the 4 directly below the 6 in 56. A vertical line is drawn through all of the lines, falling between the 0 and the 4 in "0 point four two eight" and the 2 and 8 in twenty eight.

15.2: Some Numbers Are Rational

Your teacher will give your group a set of cards. Each card will have a calculations side and an explanation side.

  1. The cards show Noah’s work calculating the fraction representation of $0.4\overline{85}$. Arrange these in order to see how he figured out that $0.4\overline{85} = \frac{481}{990}$ without needing a calculator.

  2. Use Noah’s method to calculate the fraction representation of:

    1. $0.1\overline{86}$
    2. $0.7\overline{88}$

15.3: Some Numbers Are Not Rational

    1. Why is $\sqrt{2}$ between 1 and 2 on the number line?
    2. Why is $\sqrt{2}$ between 1.4 and 1.5 on the number line?
    3. How can you figure out an approximation for $\sqrt{2}$ accurate to 3 decimal places?

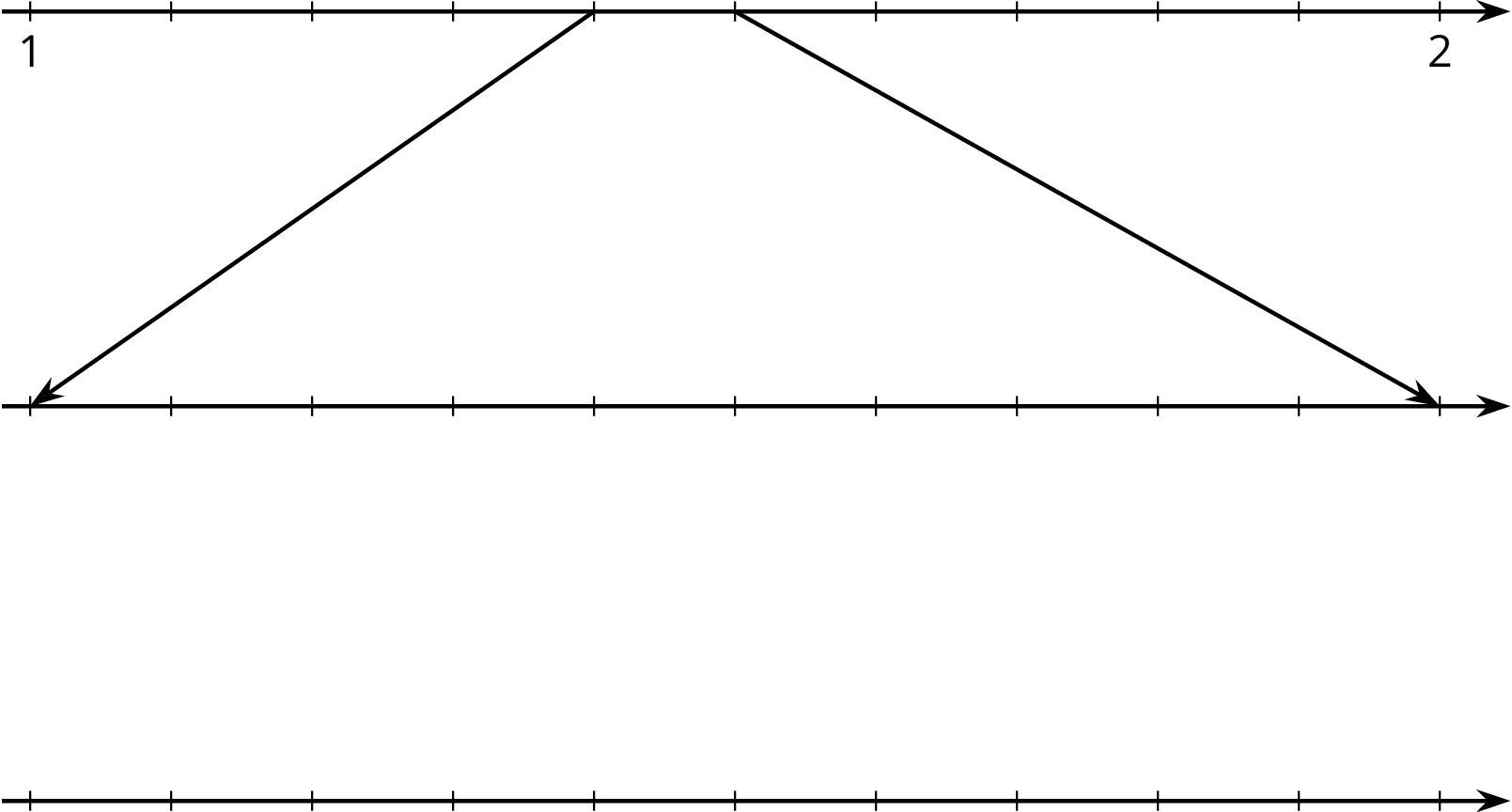
    4. Label all of the tick marks. Plot $\sqrt{2}$ on all three number lines. Make sure to add arrows from the second to the third number lines.

      A zooming number line consisting of 3 number lines, aligned vertically, each with 11 evenly spaced tick marks. On the first number line, the first tick mark is labeled "1" and the eleventh tick mark is labeled "2." Two arrows are drawn from the first number line to the second number line. The first arrow is drawn from the fifth tick mark on the first number line to the first tick mark on the second number line. The second arrow is drawn from the sixth tick mark on the first number line to the eleventh tick mark on the second number line. There are no numbers indicated on the second number line. The third number line is unlabeled.
    1. Elena notices a beaker in science class says it has a diameter of 9 cm and measures its circumference to be 28.3 cm. What value do you get for $\pi$ using these values and the equation for circumference, $C=2\pi r$?
    2. Diego learned that one of the space shuttle fuel tanks had a diameter of 840 cm and a circumference of 2,639 cm. What value do you get for $\pi$ using these values and the equation for circumference, $C=2\pi r$?

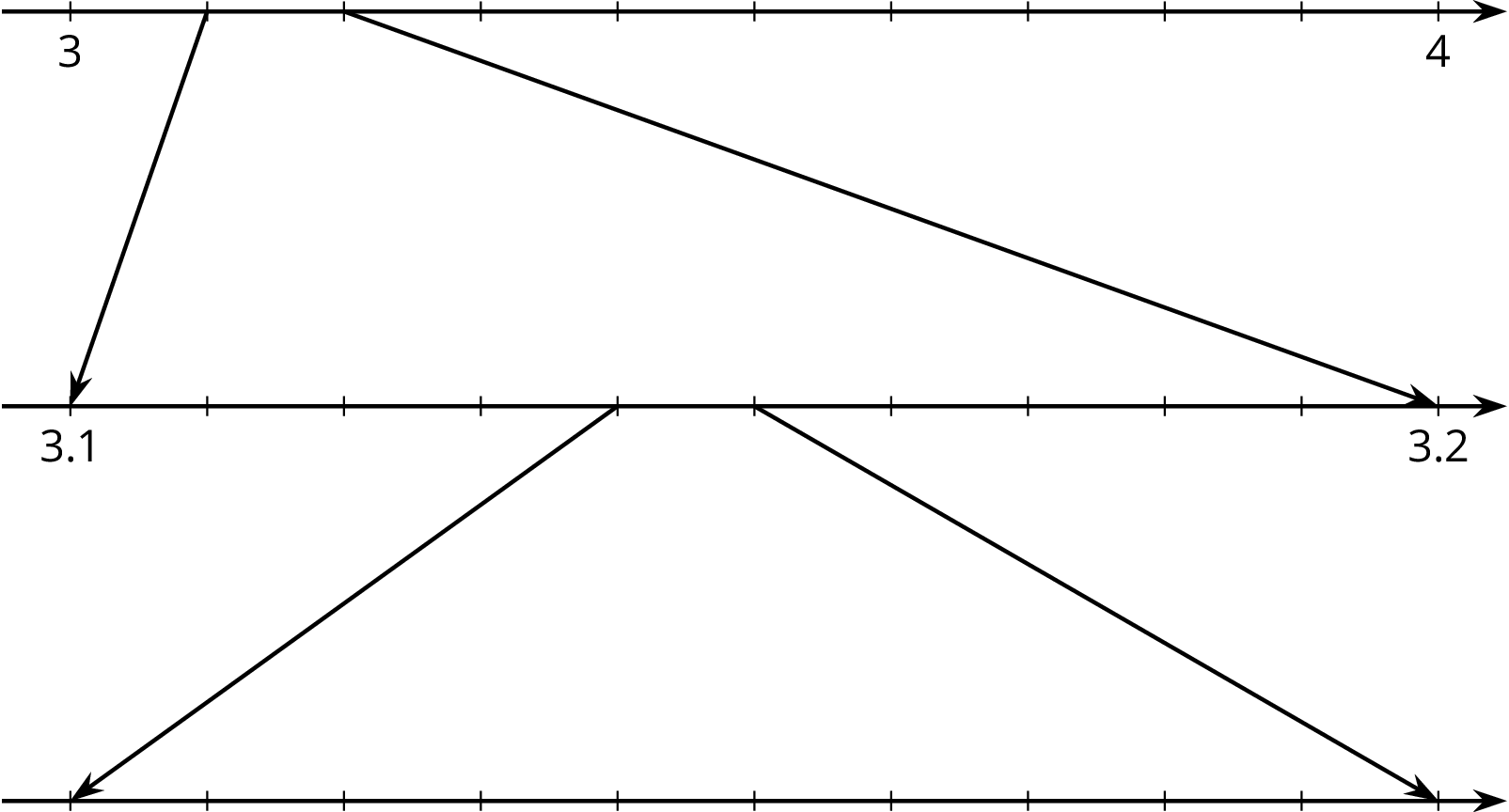
    3. Label all of the tick marks on the number lines. Use a calculator to get a very accurate approximation of $\pi$ and plot that number on all three number lines.

      A zooming number line consisting of 3 number lines, aligned vertically, each with 11 evenly spaced tick marks. On the top number line, the first tick mark is labeled "3" and the eleventh tick mark is labeled "4." Two arrows are drawn from the top number line to the middle number line. The first arrow is drawn from the second tick mark on the top number line to the first tick mark on the middle number line. The other arrow is drawn from the third tick mark on top number to the eleventh tick mark on the middle number line. On the middle number line, the first tick mark is labeled "3 point 1" and the eleventh tick mark is labeled "3 point 2." Two arrows are drawn from the middle number line to the bottom number line. The first arrow is drawn from the fifth tick mark on the middle number line to the first tick mark on the bottom number line. The other arrow is drawn from the sixth tick mark on the middle number line to the eleventh tick mark on the bottom number line. The bottom number line is not labeled.
       

    4. How can you explain the differences between these calculations of $\pi$?

Summary

Not every number is rational. Earlier we tried to find a fraction whose square is equal to 2. That turns out to be impossible, although we can get pretty close (try squaring $\frac75$). Since there is no fraction equal to $\sqrt{2}$ it is not a rational number, which is why we call it an irrational number. Another well-known irrational number is $\pi$.

Any number, rational or irrational, has a decimal expansion. Sometimes it goes on forever. For example, the rational number $\frac{2}{11}$ has the decimal expansion $0.181818 . . . $ with the 18s repeating forever. Every rational number has a decimal expansion that either stops at some point or ends up in a repeating pattern like $\frac2{11}$. Irrational numbers also have infinite decimal expansions, but they don't end up in a repeating pattern. From the decimal point of view we can see that rational numbers are pretty special. Most numbers are irrational, even though the numbers we use on a daily basis are more frequently rational.

Practice Problems ▶