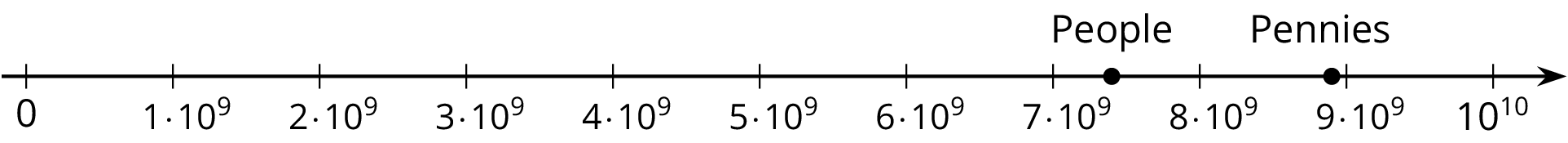10.1: Labeling Tick Marks on a Number Line
Label the tick marks on the number line. Be prepared to explain your reasoning.
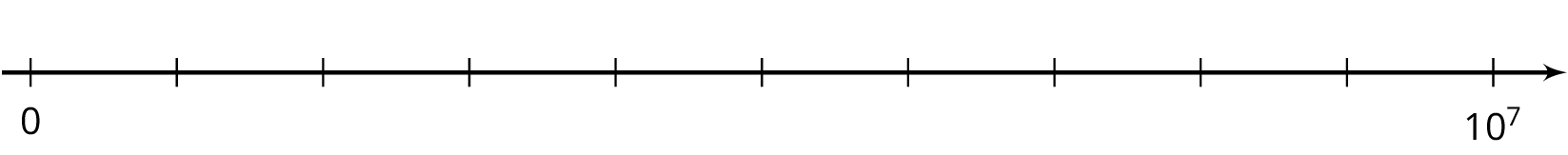
Let’s visualize large numbers on the number line using powers of 10.
Label the tick marks on the number line. Be prepared to explain your reasoning.
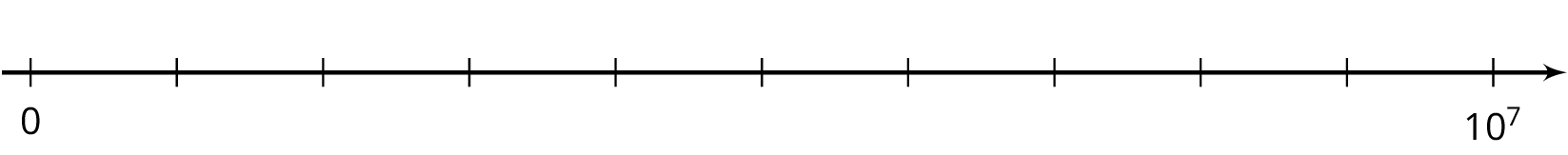
Discuss with a partner how you decided where each point should go.
The table shows how fast light waves or electricity can travel through different materials:
| material | speed of light (meters per second) | |
|---|---|---|
| Row 1 | space | 300,000,000 |
| Row 2 | water | (2.25) \boldcdot 10^8 |
| Row 3 | copper wire (electricity) | 280,000,000 |
| Row 4 | diamond | 124 \boldcdot 10^6 |
| Row 5 | ice | (2.3) \boldcdot 10^8 |
| Row 6 | olive oil | 200,000,000 |
Which is faster, light through diamond or light through ice? How can you tell from the expressions for speed?
Let’s zoom in to highlight the values between (2.0) \boldcdot 10^8 and (3.0) \boldcdot 10^8.
Plot a point for each speed on both number lines, and label it with the corresponding material.
There is one speed that you cannot plot on the bottom number line. Which is it? Plot it on the top number line instead.
The number 2,100 is close, but doesn’t quite work. The first digit is 2, and there are 2 zeros. The second digit is 1, and there is 1 one. The fourth digit is 0, and there are no threes. But the third digit, which is supposed to count the number of 2’s, is zero.
There are many ways to compare two quantities. Suppose we want to compare the world population, about
7.4 billion
to the number of pennies the U.S. made in 2015, about
8,900,000,000
There are many ways to do this. We could write 7.4 billion as a decimal, 7,400,000,000, and then we can tell that there were more pennies made in 2015 than there are people in the world! Or we could use powers of 10 to write these numbers: 7.4 \boldcdot 10^9 for people in the world and 8.9 \boldcdot 10^9 for the number of pennies.
For a visual representation, we could plot these two numbers on a number line. We need to carefully choose our end points to make sure that the numbers can both be plotted. Since they both lie between 10^9 and 10^{10}, if we make a number line with tick marks that increase by one billion, or 10^9, we start the number line with 0 and end it with 10 \boldcdot 10^{9}, or 10^{10}. Here is a number line with the number of pennies and world population plotted: