Imagine a cylinder with a radius of 5 cm that is being filled with water. As the height of the water increases, the volume of water increases.
We say that the volume of the water in the cylinder, V, depends on the height of the water h. We can represent this relationship with an equation: V= \pi \boldcdot 5^2h or just
V = 25\pi h
This equation represents a proportional relationship between the height and the volume. We can use this equation to understand how the volume changes when the height is tripled.
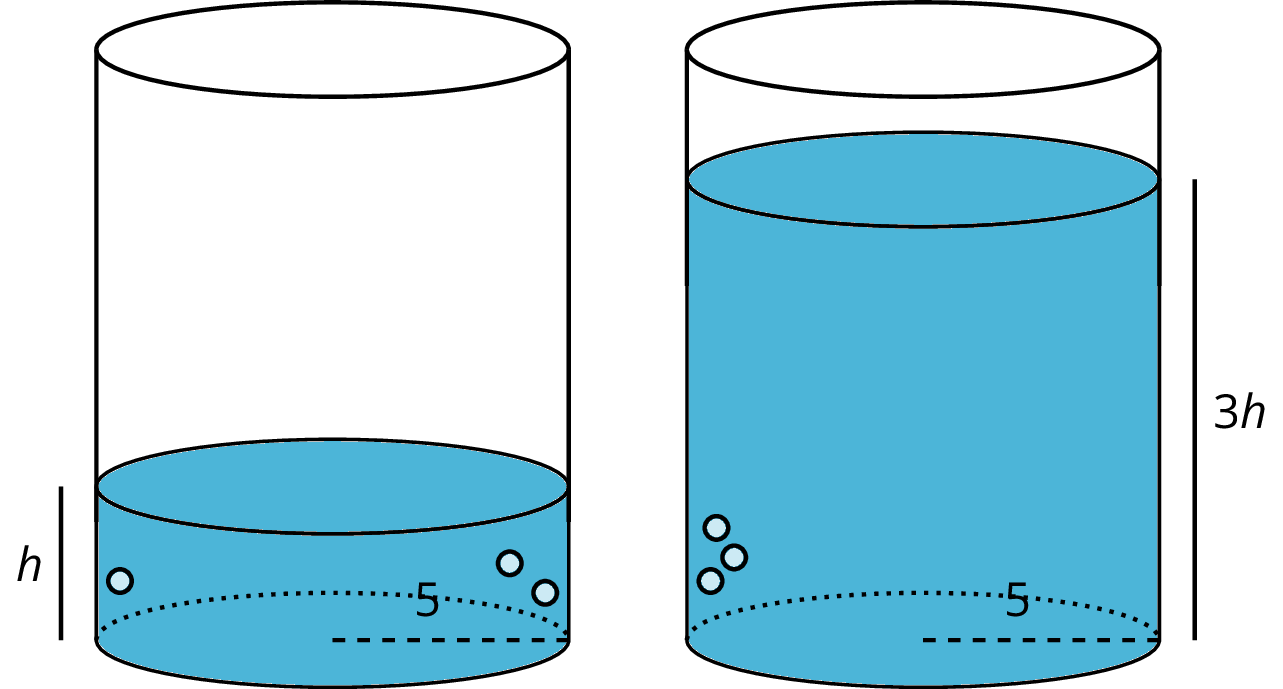
The new volume would be V = 25 \pi (3h) = 75 \pi h, which is precisely 3 times as much as the old volume of 25\pi h. In general, when one quantity in a proportional relationship changes by a given factor, the other quantity changes by the same factor.
Remember that proportional relationships are examples of linear relationships, which can also be thought of as functions. So in this example V, the volume of water in the cylinder, is a function of the height h of the water.