12.1: Missing center
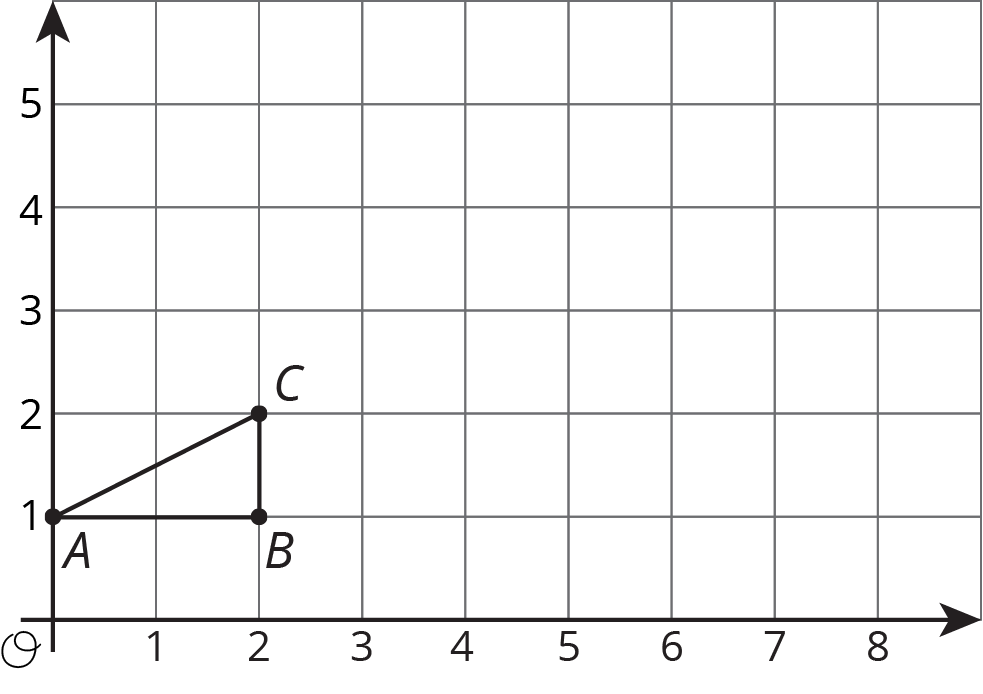
A dilation with scale factor 2 sends A to B. Where is the center of the dilation?

Let’s write equations for lines.
A dilation with scale factor 2 sends A to B. Where is the center of the dilation?

Here is a line.
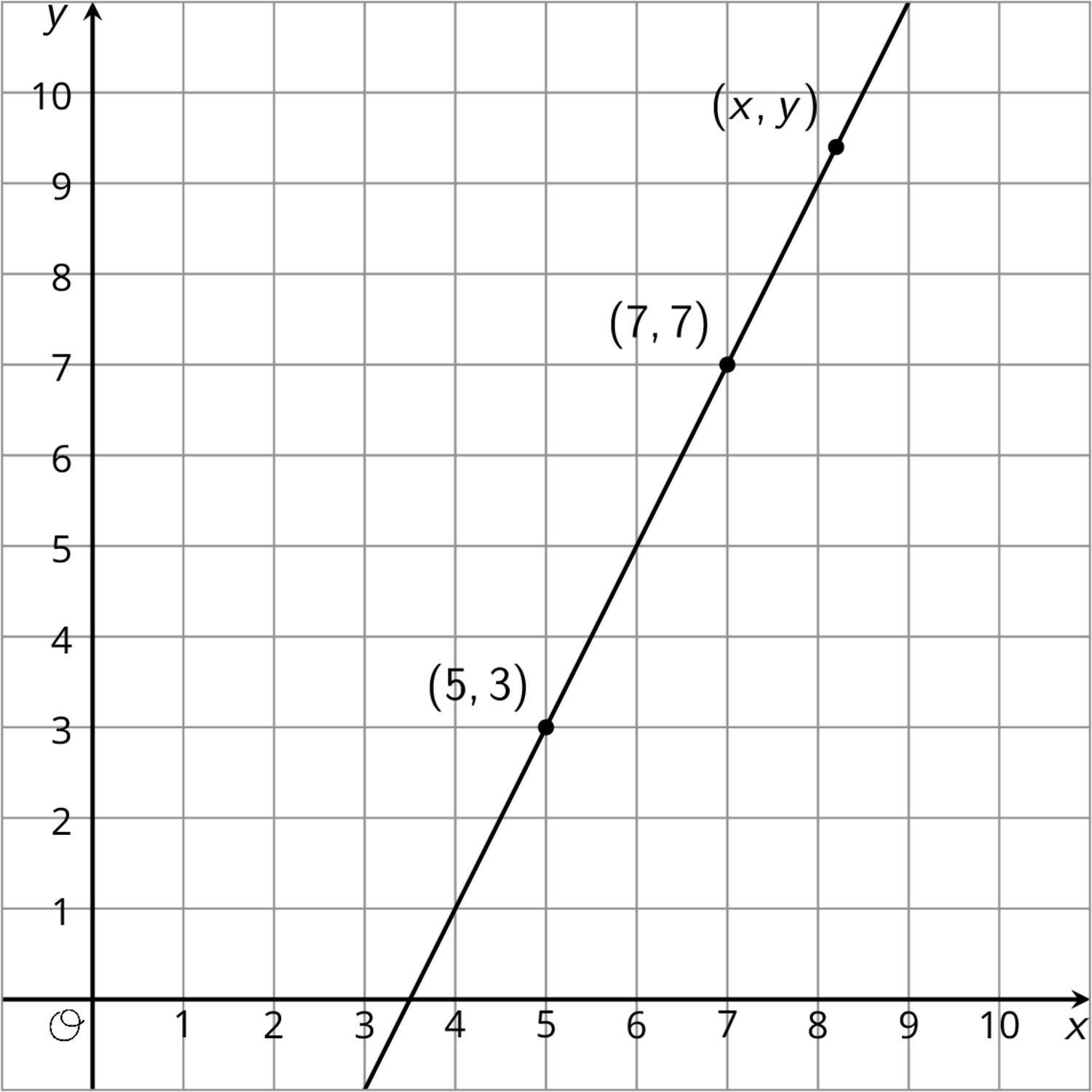
There are many different ways to write down an equation for a line like the one in the problem. Does \frac{y-3}{x-6}=2 represent the line? What about \frac{y-6}{x-4}=5? What about \frac{y+5}{x-1}=2? Explain your reasoning.
Here is triangle ABC.
We can use what we know about slope to decide if a point lies on a line. Here is a line with a few points labeled.
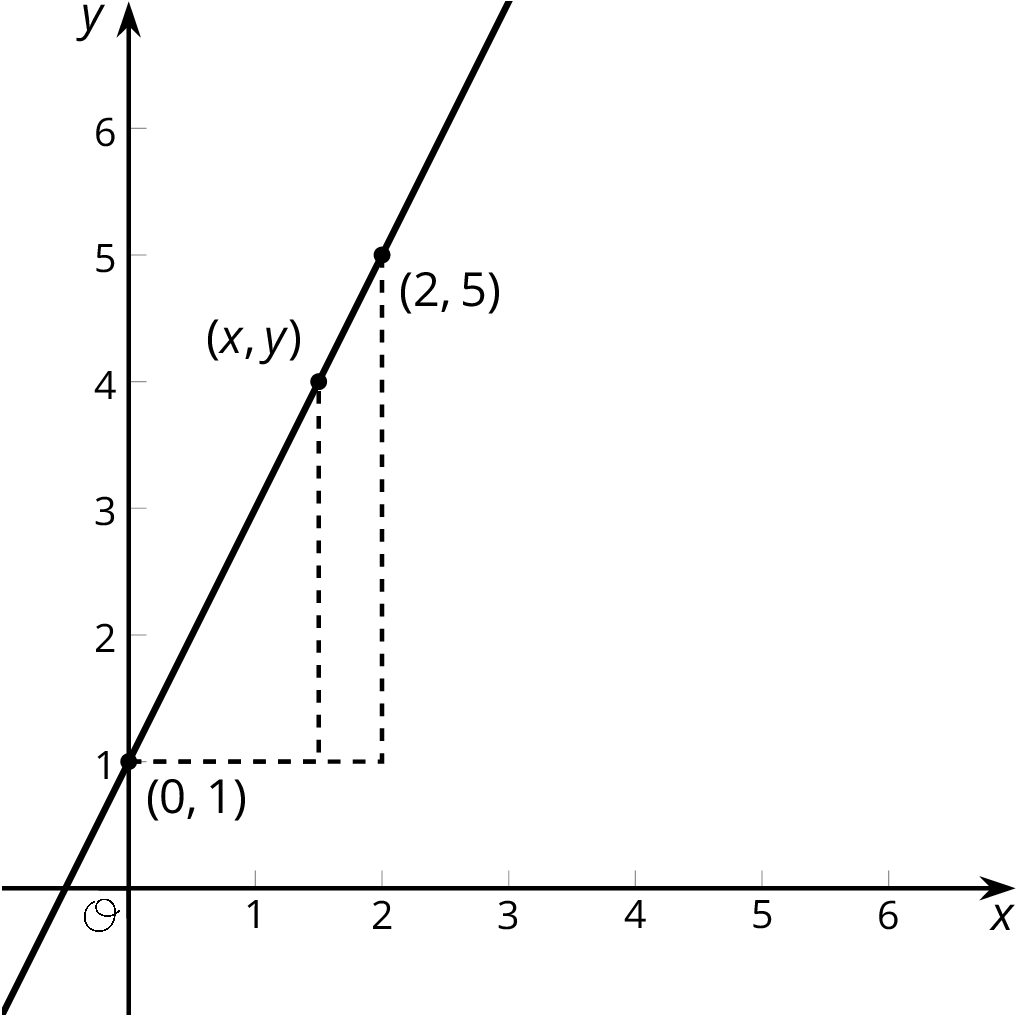
The slope triangle with vertices (0,1) and (2,5) gives a slope of \frac{5-1}{2-0} =2. The slope triangle with vertices (0,1) and (x,y) gives a slope of \frac{y-1}{x}. Since these slopes are the same, \frac{y-1}{x} = 2 is an equation for the line. So, if we want to check whether or not the point (11,23) lies on this line, we can check that \frac{23-1}{11} =2. Since (11,23) is a solution to the equation, it is on the line!