Sketch a graph of the relationship between cost and pounds of blueberries.
Unit 3: Practice Problem Sets
Lesson 1
Problem 1
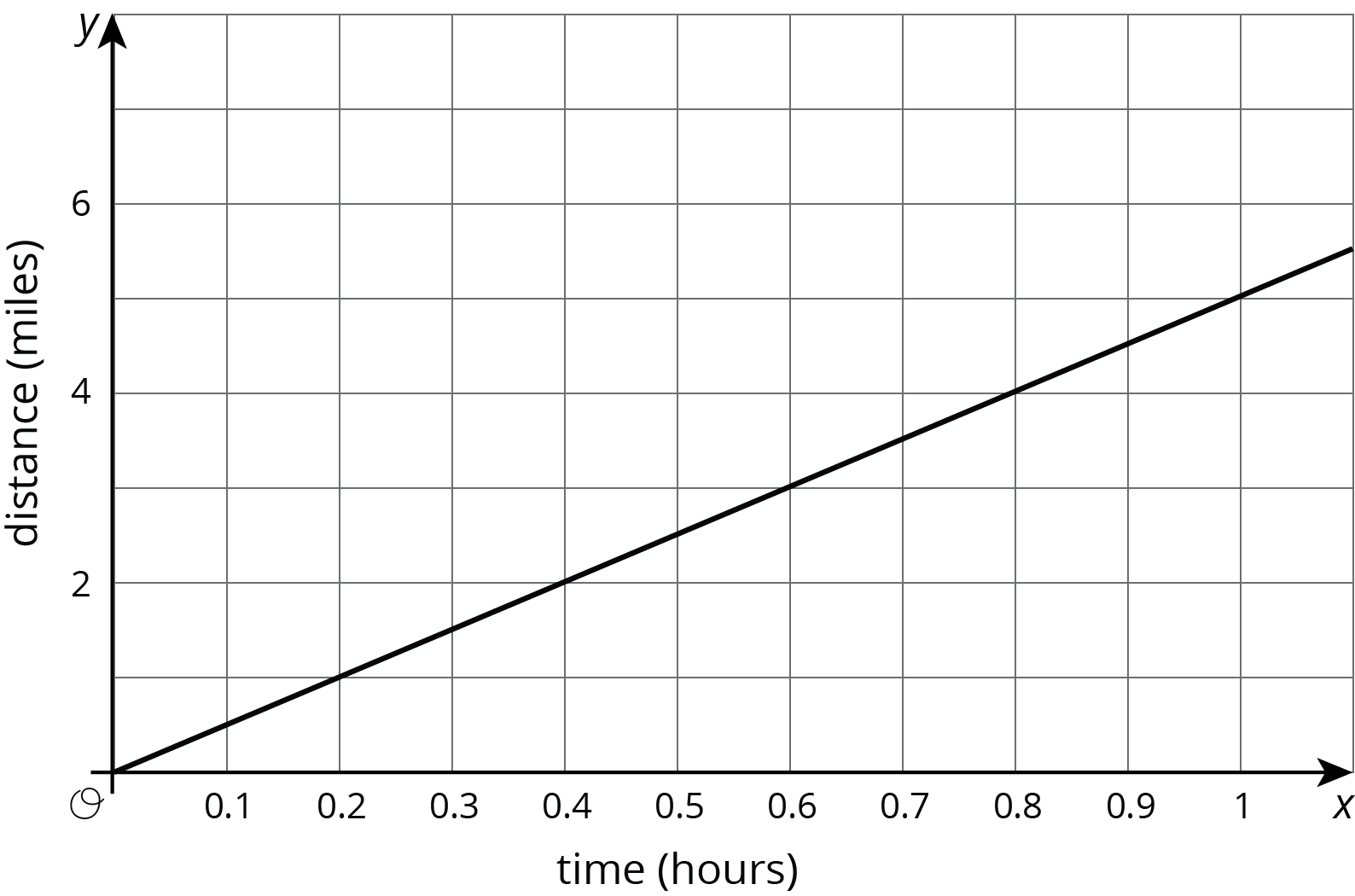
Priya jogs at a constant speed. The relationship between her distance and time is shown on the graph. Diego bikes at a constant speed twice as fast as Priya. Sketch a graph showing the relationship between Diego’s distance and time.
Problem 2
A you-pick blueberry farm offers 6 lbs of blueberries for $16.50.
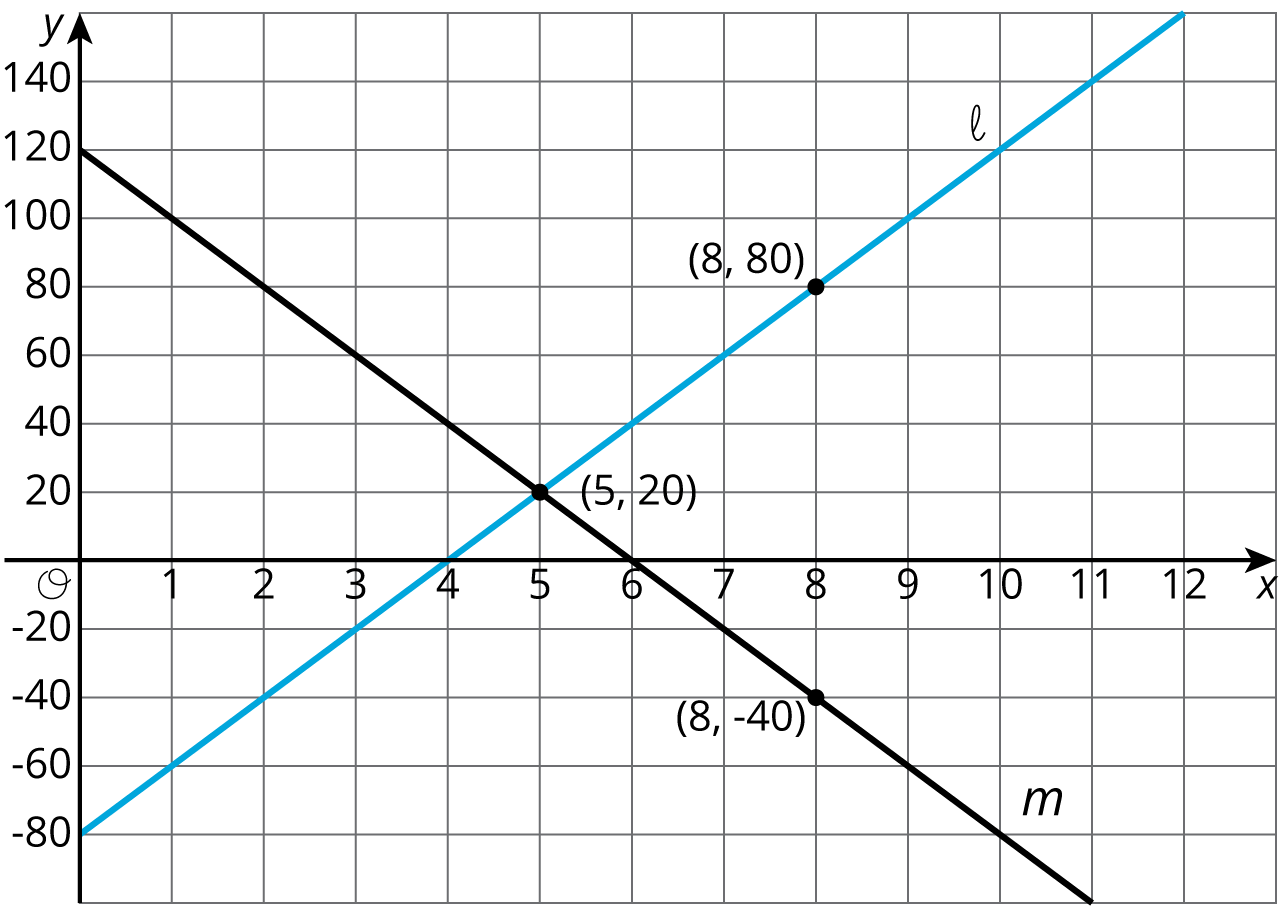
Problem 3 (from Unit 2, Lesson 12)
A line contains the points (\text-4,1) and (4,6). Decide whether or not each of these points is also on the line:
- (0,3.5)
- (12,11)
- (80,50)
- (\text-1,2.875)
Problem 4 (from Unit 2, Lesson 11)
The points (2,\text-4), (x,y), A, and B all lie on the line. Find an equation relating x and y.

Lesson 2
Problem 1
The tortoise and the hare are having a race. After the hare runs 16 miles the tortoise has only run 4 miles.
The relationship between the distance x the tortoise “runs” in miles for every y miles the hare runs is y=4x. Graph this relationship.

Problem 2
The table shows a proportional relationship between the weight on a spring scale and the distance the spring has stretched.
- Complete the table.
- Describe the scales you could use on the x and y axes of a coordinate grid that would show all the distances and weights in the table.
| distance (cm) | weight (newtons) | |
|---|---|---|
| row 1 | 20 | 28 |
| row 2 | 55 | |
| row 3 | 140 | |
| row 4 | 1 |
Problem 3 (from Unit 2, Lesson 6)
Find a sequence of rotations, reflections, translations, and dilations showing that one figure is similar to the other. Be specific: give the amount and direction of a translation, a line of reflection, the center and angle of a rotation, and the center and scale factor of a dilation.

Problem 4 (from Unit 2, Lesson 6)
Consider the following dialogue:
Andre said, “I found two figures that are congruent, so they can’t be similar.”
Diego said, “No, they are similar! The scale factor is 1.”
Who is correct? Use the definition of similarity to explain your answer.
Lesson 3
Problem 1
Here is a graph of the proportional relationship between calories and grams of fish: 
- Write an equation that reflects this relationship using x to represent the amount of fish in grams and y to represent the number of calories.
- Use your equation to complete the table:
grams of fish number of calories row 1 1000 row 2 2001 row 3 1
Problem 2
Students are selling raffle tickets for a school fundraiser. They collect $24 for every 10 raffle tickets they sell.
- Suppose M is the amount of money the students collect for selling R raffle tickets. Write an equation that reflects the relationship between M and R.
- Label and scale the axes and graph this situation with M on the vertical axis and R on the horizontal axis. Make sure the scale is large enough to see how much they would raise if they sell 1000 tickets.

Problem 3 (from Unit 2, Lesson 10)
Describe how you can tell whether a line’s slope is greater than 1, equal to 1, or less than 1.
Problem 4 (from Unit 2, Lesson 12)
A line is represented by the equation \frac{y}{x-2}=\frac{3}{11}. What are the coordinates of some points that lie on the line? Graph the line on graph paper.
Lesson 4
Problem 1
A contractor must haul a large amount of dirt to a work site. She collected information from two hauling companies. EZ Excavation gives its prices in a table. Happy Hauling Service gives its prices in a graph.
| dirt (cubic yards) | cost (dollars) | |
|---|---|---|
| row 1 | 8 | 196 |
| row 2 | 20 | 490 |
| row 3 | 26 | 637 |
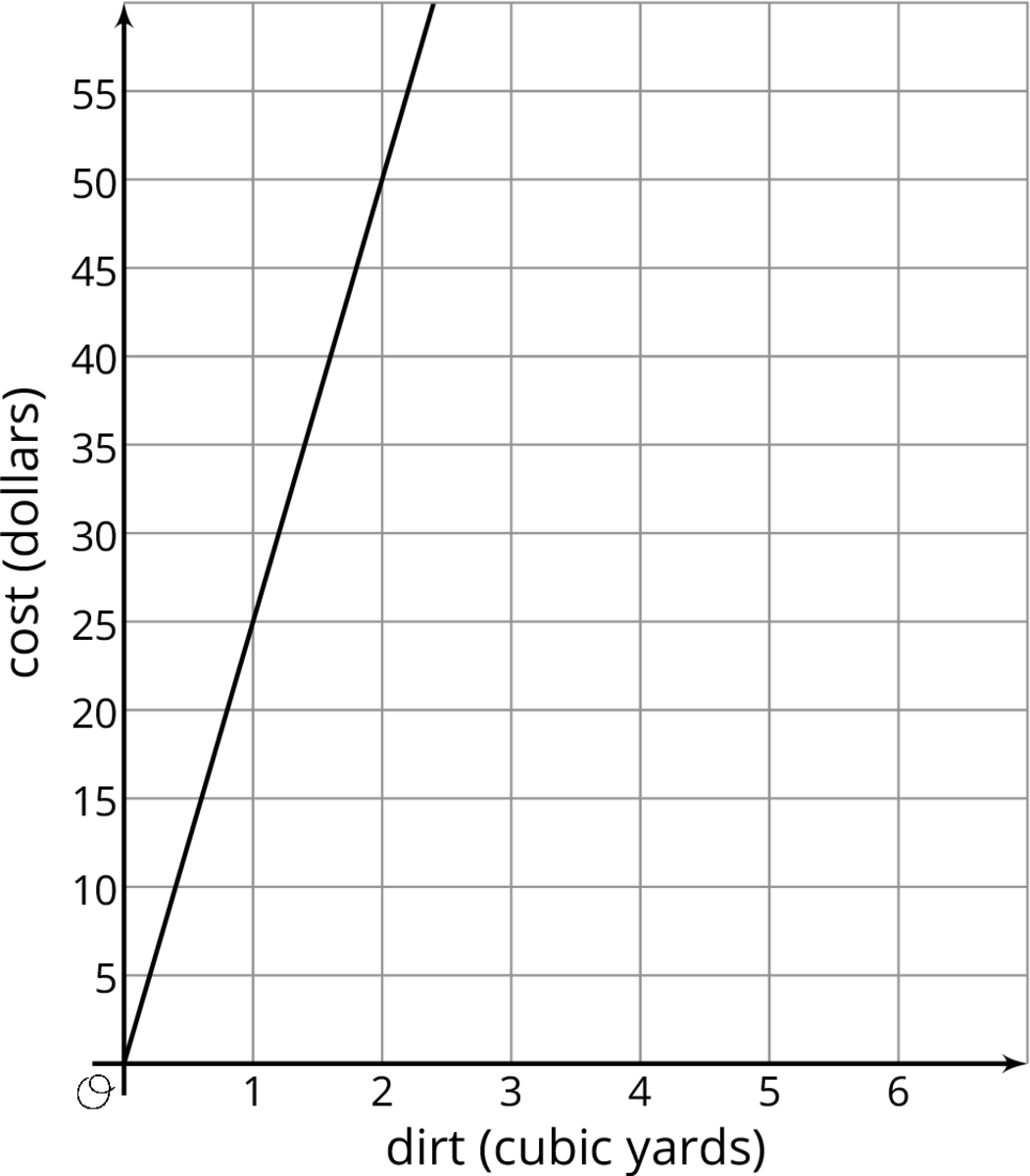
- How much would each hauling company charge to haul 40 cubic yards of dirt? Explain or show your reasoning.
- Calculate the rate of change for each relationship. What do they mean for each company?
- If the contractor has 40 cubic yards of dirt to haul and a budget of $1000, which hauling company should she hire? Explain or show your reasoning.
Problem 2
Andre and Priya are tracking the number of steps they walk. Andre records that he can walk 6000 steps in 50 minutes. Priya writes the equation y=118x, where y is the number of steps and x is the number of minutes she walks, to describe her step rate. This week, Andre and Priya each walk for a total of 5 hours. Who walks more steps? How many more?
Problem 3 (from Unit 2, Lesson 11)
Find the coordinates of point D in each diagram:
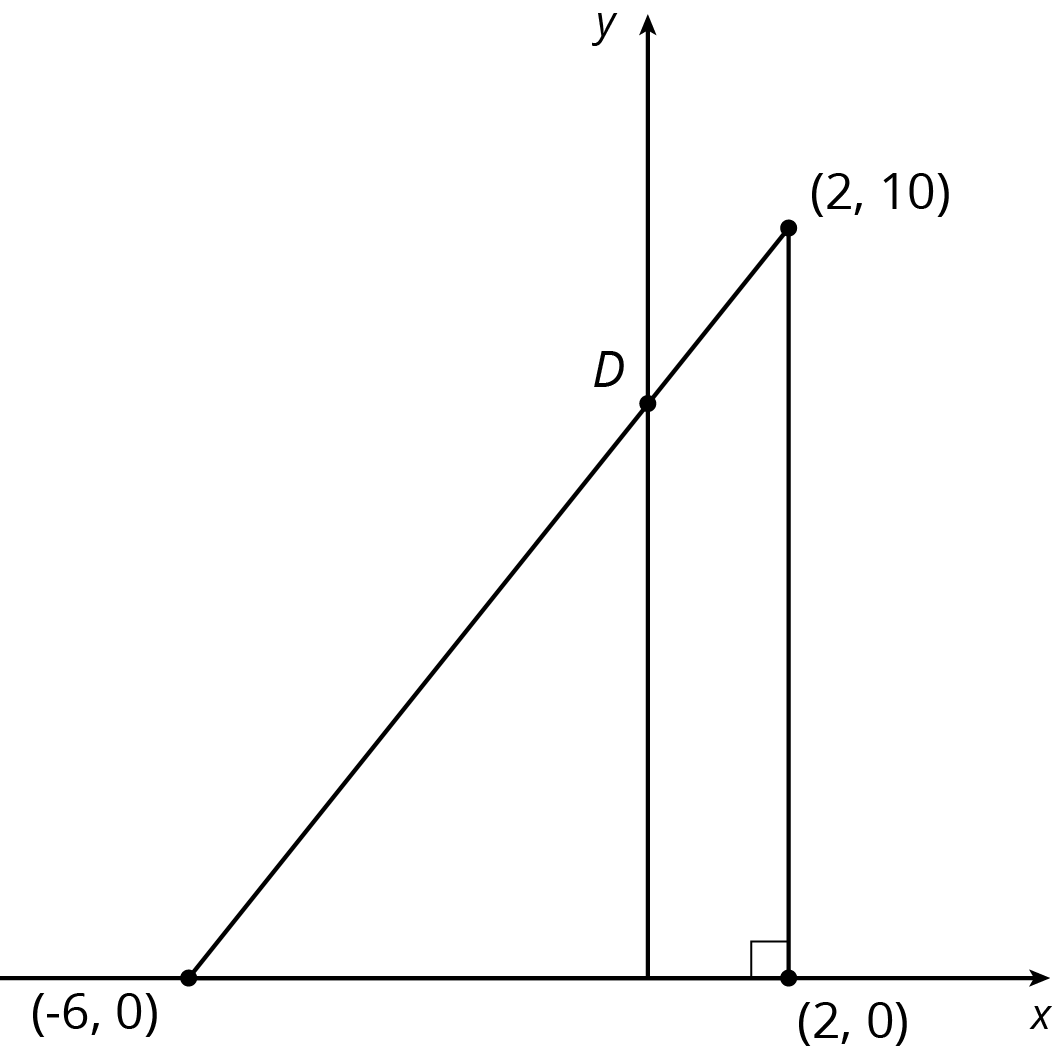
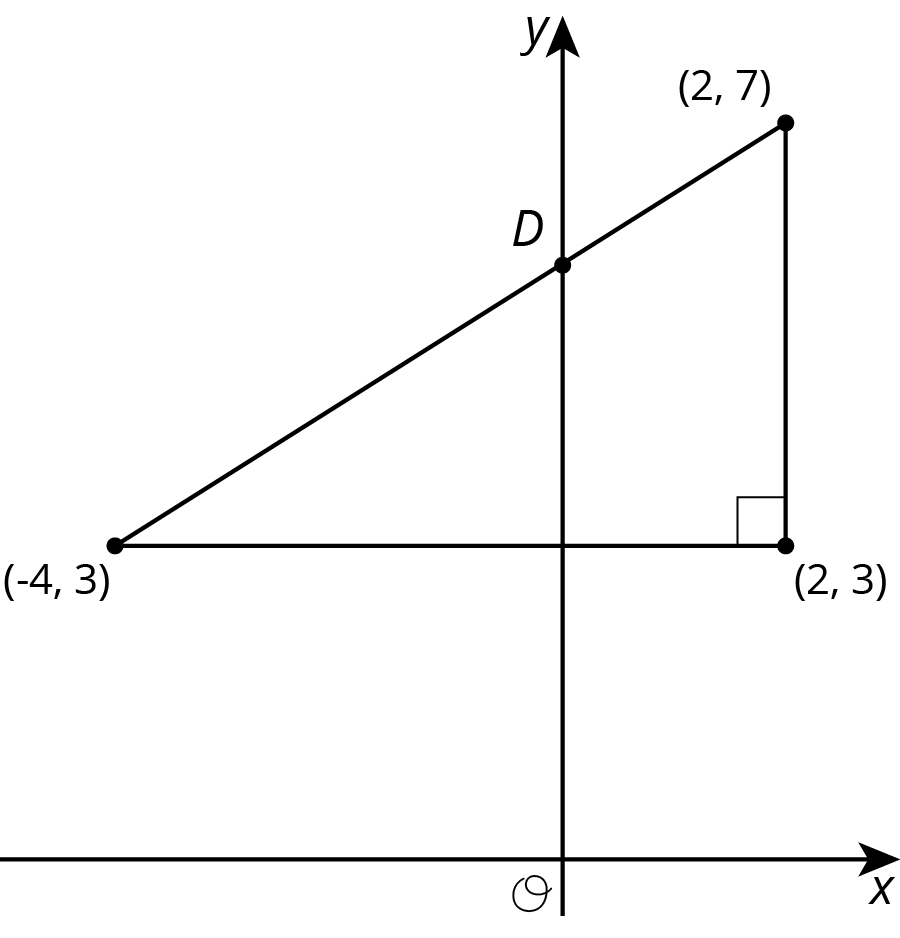
Problem 4 (from Unit 2, Lesson 11)
Select all the pairs of points so that the line between those points has slope \frac 2 3.
- (0,0) and (2,3)
- (0,0) and (3,2)
- (1,5) and (4,7)
- (\text-2,\text-2) and (4,2)
- (20,30) and (\text-20,\text-30)
Lesson 5
Problem 1
A restaurant offers delivery for their pizzas. The total cost is a delivery fee added to the price of the pizzas. One customer pays $25 to have 2 pizzas delivered. Another customer pays $58 for 5 pizzas. How many pizzas are delivered to a customer who pays $80?
Problem 2
To paint a house, a painting company charges a flat rate of $500 for supplies, plus $50 for each hour of labor.

- How much would the painting company charge to paint a house that needs 20 hours of labor? A house that needs 50 hours?
- Draw a line representing the relationship between x, the number of hours it takes the painting company to finish the house, and y, the total cost of painting the house. Label the two points from the earlier question on your graph.
- Find the slope of the line. What is the meaning of the slope in this context?
Problem 3 (from Unit 3, Lesson 4)
Tyler and Elena are on the cross country team.
Tyler's distances and times for a training run are shown on the graph.
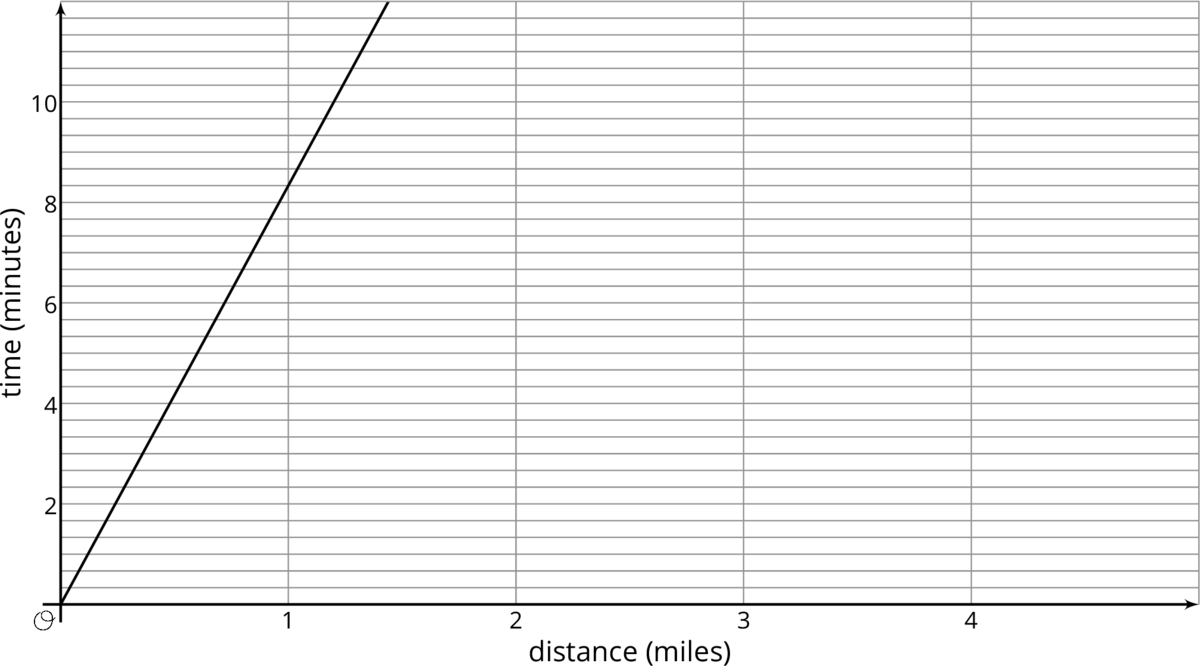
Elena’s distances and times for a training run are given by the equation y=8.5x, where x represents distance in miles and y represents time in minutes.
- Who ran farther in 10 minutes? How much farther? Explain how you know.
- Calculate each runner's pace in minutes per mile.
- Who ran faster during the training run? Explain or show your reasoning.
Problem 4 (from Unit 2, Lesson 12)
Write an equation for the line that passes through (2,5) and (6,7).
Lesson 6
Problem 1
Explain what the slope and intercept mean in each situation.
- A graph represents the perimeter, y, in units, for an equilateral triangle with side length x units. The slope of the line is 3 and the y-intercept is 0.
- The amount of money, y, in a cash box after x tickets are purchased for carnival games. The slope of the line is \frac14 and the y-intercept is 8.
- The number of chapters read, y, after x days. The slope of the line is \frac54 and the y-intercept is 2.
- The graph shows the cost in dollars, y, of a muffin delivery and the number of muffins, x, ordered. The slope of the line is 2 and the y-intercept is 3.
Problem 2 (from Unit 3, Lesson 4)
The graph shows the relationship between the number of cups of flour and the number of cups of sugar in Lin’s favorite brownie recipe.

The table shows the amounts of flour and sugar needed for Noah’s favorite brownie recipe.
| amount of sugar (cups) | amount of flour (cups) | |
|---|---|---|
| row 1 | \frac32 | 1 |
| row 2 | 3 | 2 |
| row 3 | 4\frac12 | 3 |
- Noah and Lin buy a 12-cup bag of sugar and divide it evenly to make their recipes. If they each use all their sugar, how much flour do they each need?
- Noah and Lin buy a 10-cup bag of flour and divide it evenly to make their recipes. If they each use all their flour, how much sugar do they each need?
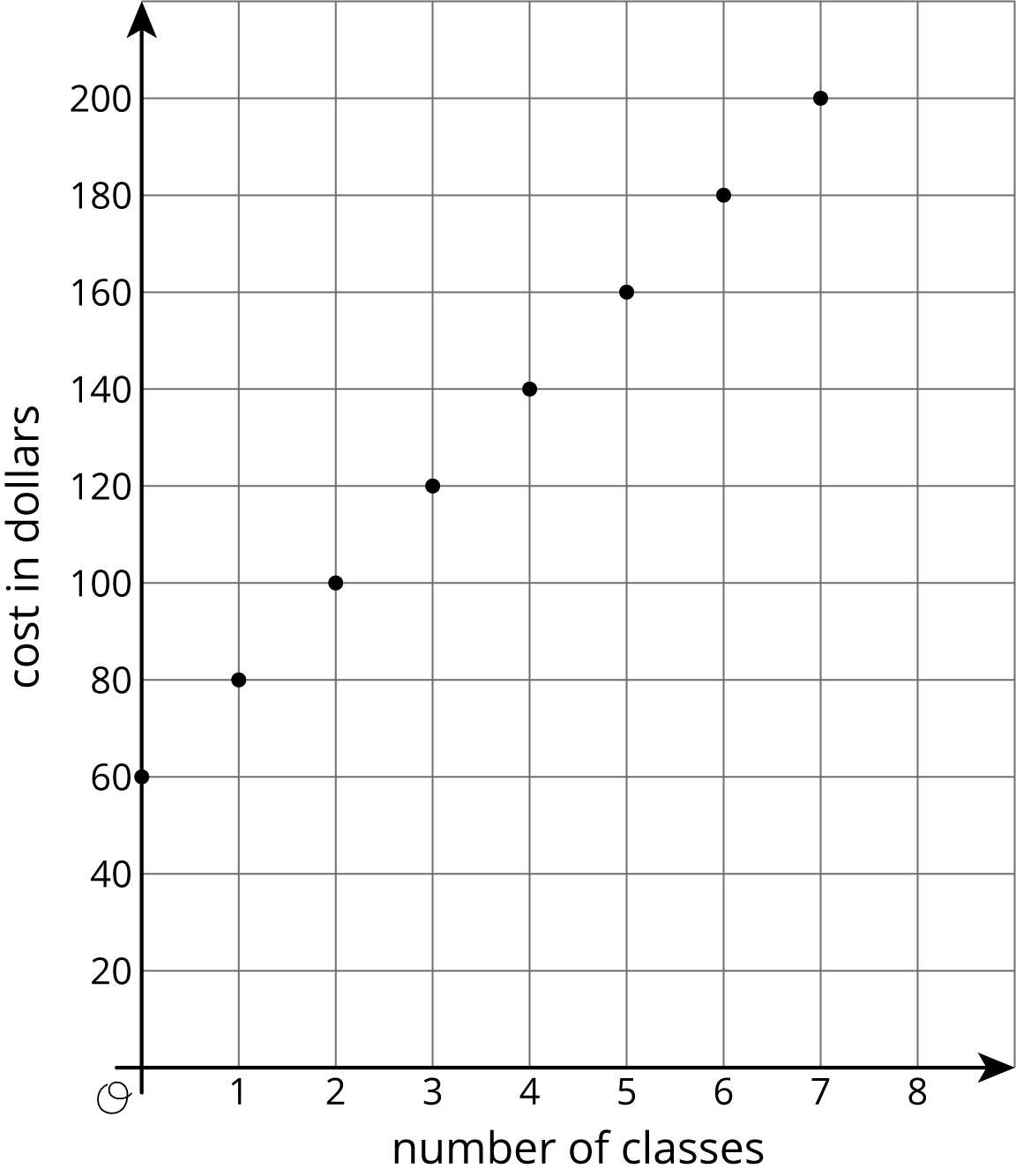
Problem 3
Customers at the gym pay a membership fee to join and then a fee for each class they attend. Here is a graph that represents the situation.
- What does the slope of the line shown by the points mean in this situation?
- What does the vertical intercept mean in this situation?
Lesson 7
Problem 1 (from Unit 3, Lesson 4)
Here are recipes for two different banana cakes. Information for the first recipe is shown in the table.
| sugar (cups) | flour (cups) | |
|---|---|---|
| row 1 | \frac12 | \frac34 |
| row 2 | 2\frac12 | 3\frac34 |
| row 3 | 3 | 4\frac12 |
The relationship between cups of flour y and cups of sugar x in the second recipe is y=\frac74x
- If you used 4 cups of sugar, how much flour does each recipe need?
- What is the constant of proportionality for each situation and what does it mean?
Problem 2 (from Unit 2, Lesson 6)
Show that the two figures are similar by identifying a sequence of translations, rotations, reflections, and dilations that takes the larger figure to the smaller one.

Problem 3
Create a graph that shows three linear relationships with different y-intercepts using the following slopes, and write an equation for each line.
Slopes:
- \frac15
- \frac35
- \frac65

Problem 4
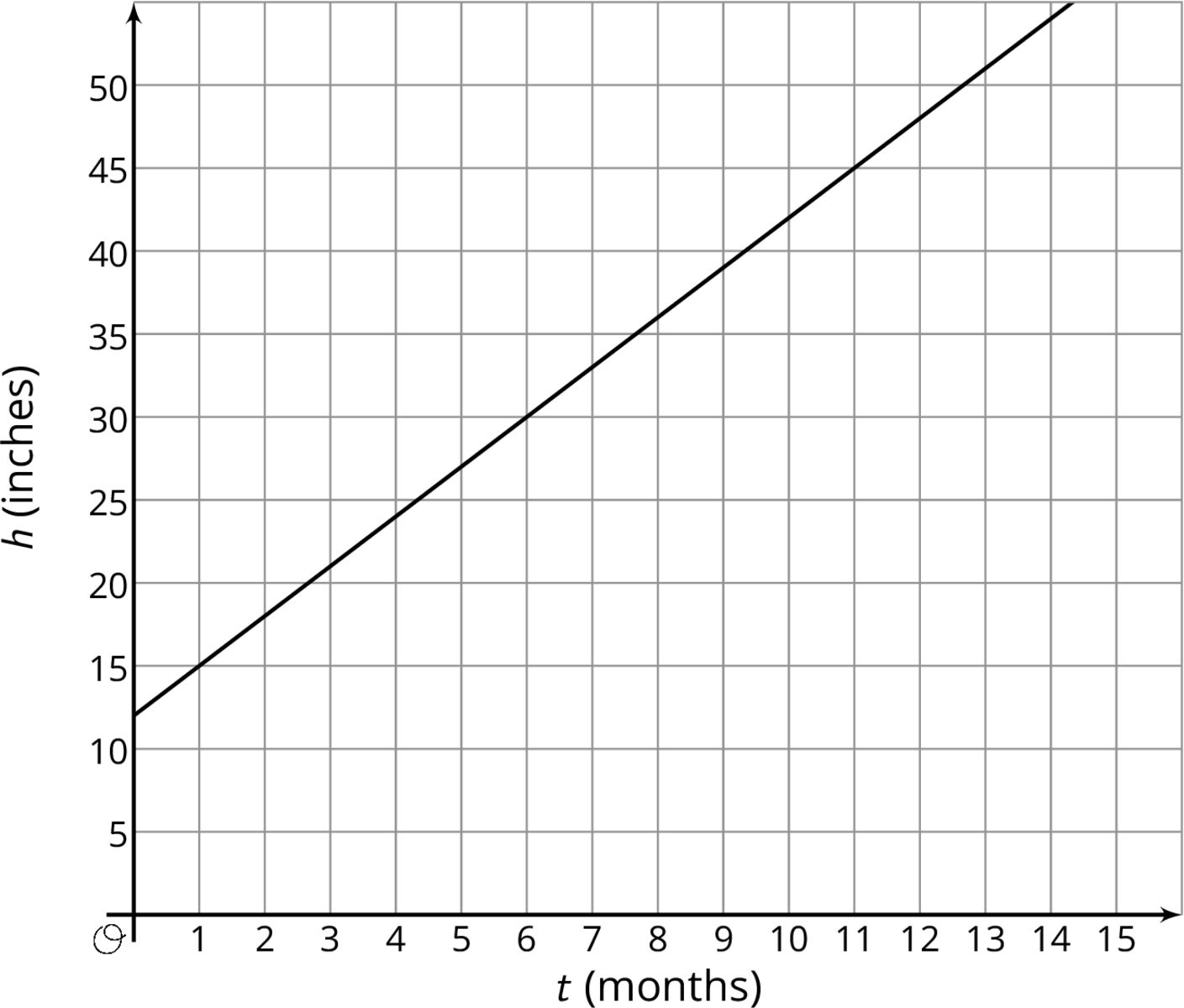
The graph shows the height in inches, h, of a bamboo plant t months after it has been planted.
- Write an equation that describes the relationship between h and t.
- After how many months will the bamboo plant be 66 inches tall? Explain or show your reasoning.
Lesson 8
Problem 1
Select all equations that have graphs with the same y-intercept.
- y=3x -8
- y=3x -9
- y=3x+8
- y=5x -8
- y=2x -8
- y=\frac13x -8
Problem 2
Create a graph showing the equations y=\frac14x and y=\frac14x-5. Explain how the graphs are the same and how they are different.
Problem 3
A cable company charges $70 per month for cable service to existing customers.
- Find a linear equation representing the relationship between x, the number of months of service, and y, the total amount paid in dollars by an existing customer.
- For new customers, there is an additional one-time $100 service fee. Repeat the previous problem for new customers.
- When the two equations are graphed in the coordinate plane, how are they related to each other geometrically?
Problem 4 (from Unit 3, Lesson 6)
Match each graph to a situation.

- The graph represents the perimeter, y, in units, for an equilateral triangle with side length of x units. The slope of the line is 3.
- The amount of money, y, in a cash box after x tickets are purchased for carnival games. The slope of the line is \frac14.
- The number of chapters read, y, after x days. The slope of the line is \frac54.
- The graph shows the cost in dollars, y, of a muffin delivery and the number of muffins, x, ordered. The slope of the line is 2.
Problem 5 (from Unit 3, Lesson 6)
A mountain road is 5 miles long and gains elevation at a constant rate. After 2 miles, the elevation is 5500 feet above sea level. After 4 miles, the elevation is 6200 feet above sea level.
- Find the elevation of the road at the point where the road begins.
- Describe where you would see the point in part (a) on a graph where y represents the elevation in feet and x represents the distance along the road in miles.
Lesson 9
Problem 1
Suppose that during its flight, the elevation e (in feet) of a certain airplane and its time t, in minutes since takeoff, are related by a linear equation. Consider the graph of this equation, with time represented on the horizontal axis and elevation on the vertical axis. For each situation, decide if the slope is positive, zero, or negative.
- The plane is cruising at an altitude of 37,000 feet above sea level.
- The plane is descending at rate of 1000 feet per minute.
- The plane is ascending at a rate of 2000 feet per minute.
Problem 2 (from Unit 3, Lesson 7)
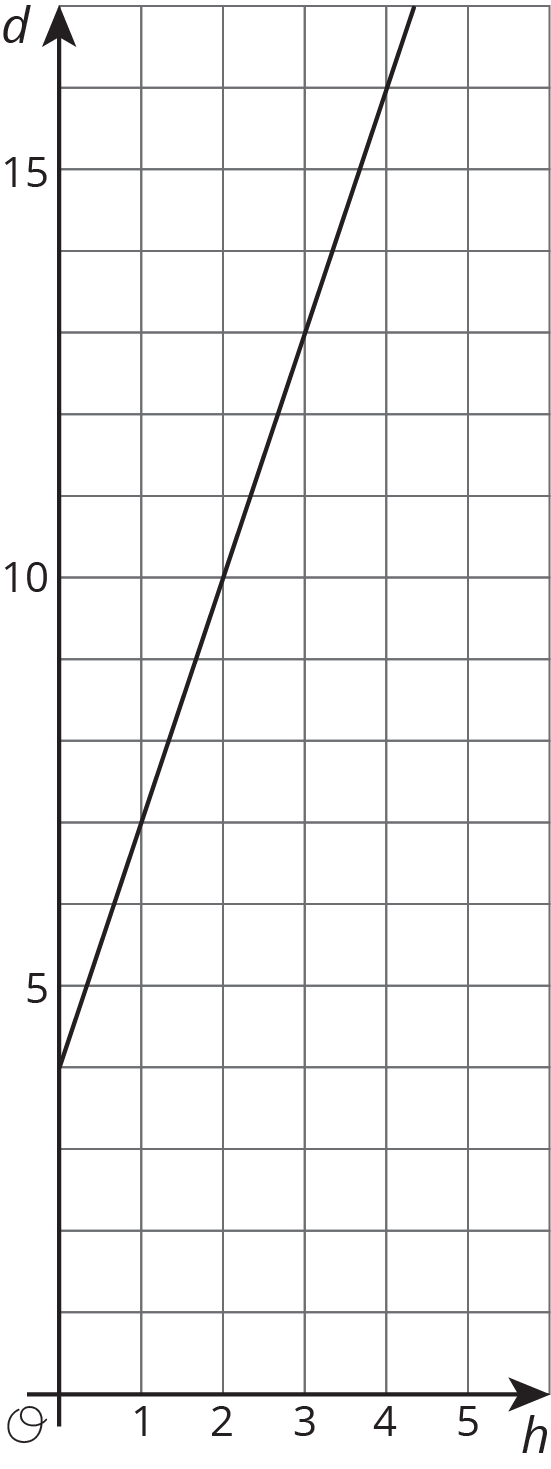
A group of hikers park their car at a trail head and hike into the forest to a campsite. The next morning, they head out on a hike from their campsite walking at a steady rate. The graph shows their distance in miles, d, from the car on the day of their hike after h hours.
- How far is the campsite from their car? Explain how you know.
- Write an equation that describes the relationship between d and h.
- After how many hours will the hikers be 16 miles from their car? Explain or show your reasoning.
Problem 3 (from Unit 3, Lesson 4)
Elena’s aunt pays her $1 for each call she makes to let people know about her aunt’s new business. The table shows how much money Diego receives for washing windows for his neighbors.
| number of windows | number of dollars | |
|---|---|---|
| row 1 | 27 | 30 |
| row 2 | 45 | 50 |
| row 3 | 81 | 90 |
Select all the statements about the situation that are true.
- Elena makes more money for making 10 calls than Diego makes for washing 10 windows.
- Diego makes more money for washing each window than Elena makes for making each call.
- Elena makes the same amount of money for 20 calls as Diego makes for 18 windows.
- Diego needs to wash 35 windows to make as much money as Elena makes for 40 calls.
- The equation y=\frac{9}{10}x, where y is number of dollars and x is number of windows, represents Diego’s situation.
- The equation y=x, where y is the number of dollars and x is the number of calls, represents Elena’s situation.
Problem 4
Each square on a grid represents 1 unit on each side. Match the numbers with the slopes of the lines.

- \text-\frac14
- \frac14
- 4
Lesson 10
Problem 1
For each graph, calculate the slope of the line.

Problem 2
Match each pair of points to the slope of the line that joins them.
- 4
- \text-3
- \text-\frac52
- \frac67
- (9,10) and (7,2)
- (\text-8,\text-11) and (\text-1,\text-5)
- (5,\text-6) and (2,3)
- (6,3) and (5,\text-1)
- (4,7) and (6,2)
Problem 3
Draw a line with the given slope through the given point. What other point lies on that line? 
- Point A, slope = \text-3
- Point A, slope = \frac {\text{-}1}{4}
- Point C, slope = \frac {\text{-}1}{2}
- Point E, slope = \frac {\text{-}2}{3}
Problem 4 (from Unit 3, Lesson 8)
Make a sketch of a linear relationship with a slope of 4 and a negative y-intercept. Show how you know the slope is 4 and write an equation for the line.
Lesson 11
Problem 1
Suppose you wanted to graph the equation y=\text-4x-1.
- Describe the steps you would take to draw the graph.
- How would you check that the graph you drew is correct?
Problem 2
Draw the following lines and then write an equation for each.
- Slope is 0, y-intercept is 5
- Slope is 2, y-intercept is \text-1
- Slope is \text-2, y-intercept is 1
- Slope is \frac {\text{-}1}{2}, y-intercept is \text-1

Problem 3
Write an equation for each line.

Problem 4 (from Unit 3, Lesson 7)
A publisher wants to figure out how thick their new book will be. The book has a front cover and a back cover, each of which have a thickness of \frac{1}{4} of an inch. They have a choice of which type of paper to print the book on.
- Bond paper has a thickness of \frac{1}{4} inch per one hundred pages. Write an equation for the width of the book, y, if it has x hundred pages, printed on bond paper.
- Ledger paper has a thickness of \frac{2}{5} inch per one hundred pages. Write an equation for the width of the book, y, if it has x hundred pages, printed on ledger paper.
- If they instead chose front and back covers of thickness \frac{1}{3} of an inch, how would this change the equations in the previous two parts?
Lesson 12
Problem 1
Select all of the ordered pairs (x,y) that are solutions to the linear equation 2x+3y=6.
- (0,2)
- (0,6)
- (2,3)
- (3,\text-2)
- (3,0)
- (6,\text-2)
Problem 2
The graph shows a linear relationship between x and y.
x represents the number of comic books Priya buys at the store, all at the same price, and y represents the amount of money (in dollars) Priya has after buying the comic books.

- Find and interpret the x- and y-intercepts of this line.
- Find and interpret the slope of this line.
- Find an equation for this line.
- If Priya buys 3 comics, how much money will she have remaining?
Problem 3
Match each equation with its three solutions.
- y = 1.5x
- 2x + 3y = 7
- x - y = 4
- 3x = \frac y2
- y = \text-x + 1
- (14, 21), (2,3), (8,12)
- (\text-3, \text-7), (0, \text-4), (\text-1,\text-5)
- \left(\frac 12,\frac 12\right), \left(\frac 14, \frac 34\right), \left(\frac 18, \frac78\right)
- \left(1, 1\frac23\right), \left(\text-1,3\right), \left(0, 2\frac13\right)
- (0.5,3), (1,6), (1.2, 7.2)
Problem 4 (from Unit 3, Lesson 10)
A container of fuel dispenses fuel at the rate of 5 gallons per second. If y represents the amount of fuel remaining in the container, and x represents the number of seconds that have passed since the fuel started dispensing, then x and y satisfy a linear relationship.
In the coordinate plane, will the slope of the line representing that relationship have a positive, negative, or zero slope? Explain how you know.
Problem 5 (from Unit 3, Lesson 5)
A sandwich store charges a delivery fee to bring lunch to an office building. One office pays $33 for 4 turkey sandwiches. Another office pays $61 for 8 turkey sandwiches. How much does each turkey sandwich add to the cost of the delivery? Explain how you know.
Lesson 13
Problem 1
For each equation, find y when x=\text-3. Then find x when y=2
- y=6x+8
- y=\frac23x
- y=\text-x+5
- y=\frac34x-2\frac12
- y=1.5x +11
Problem 2 (from Unit 3, Lesson 9)
Match each graph of a linear relationship to a situation that most reasonably reflects its context.

- y is the weight of a kitten x days after birth.
- y is the distance left to go in a car ride after x hours of driving at a constant rate toward its destination.
- y is the temperature, in degrees C, of a gas being warmed in a laboratory experiment.
- y is the amount of calories consumed eating x crackers.
Problem 3
Problem 4
Here is a linear equation: y=\frac14 x +\frac54
- Are (1,1.5) and (12,4) solutions to the equation? Explain or show your reasoning.
- Find the x-intercept of the graph of the equation. Explain or show your reasoning.
Problem 5 (from Unit 2, Lesson 11)
Find the coordinates of B, C, and D given that AB = 5 and BC = 10.

Lesson 14
Problem 1
The owner of a new restaurant is ordering tables and chairs. He wants to have only tables for 2 and tables for 4. The total number of people that can be seated in the restaurant is 120.
- Describe some possible combinations of 2-seat tables and 4-seat tables that will seat 120 customers. Explain how you found them.
- Write an equation to represent the situation. What do the variables represent?
- Create a graph to represent the situation.
- What does the slope tell us about the situation?
- Interpret the x and y intercepts in the situation.
Problem 2 (from Unit 3, Lesson 13)
Triangle A is an isosceles triangle with two angles of measure x degrees and one angle of measure y degrees.
- Find three combinations of x and y that make this sentence true.
- Write an equation relating x and y.
- If you were to sketch the graph of this linear equation, what would its slope be? How can you interpret the slope in the context of the triangle?
Problem 3 (from Unit 3, Lesson 12)
Select all the equations for which (\text-6,\text-1) is a solution.
- y=4x+23
- 3x=\frac12y
- 2x-13y=1
- 3y=\frac12x
- 2x+6y=\text-6
Problem 4 (from Unit 3, Lesson 10)
Consider the following graphs of linear equations. Decide which line has a positive slope, and which has a negative slope. Then calculate each line’s exact slope.