The Pythagorean Theorem can be used to solve any problem that can be modeled with a right triangle where the lengths of two sides are known and the length of the other side needs to be found. For example, let’s say a cable is being placed on level ground to support a tower. It’s a 17-foot cable, and the cable should be connected 15 feet up the tower. How far away from the bottom of the tower should the other end of the cable connect to the ground?
It is often very helpful to draw a diagram of a situation, such as the one shown here:
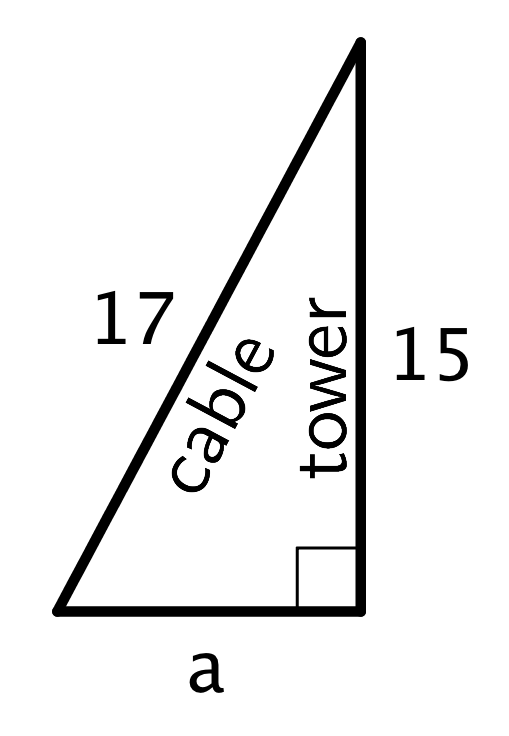
It’s assumed that the tower makes a right angle with the ground. Since this is a right triangle, the relationship between its sides is $a^2+b^2=c^2$, where $c$ represents the length of the hypotenuse and $a$ and $b$ represent the lengths of the other two sides. The hypotenuse is the side opposite the right angle. Making substitutions gives $a^2+15^2=17^2$. Solving this for $a$ gives $a=8$. So, the other end of the cable should connect to the ground 8 feet away from the bottom of the tower.