To review, the side length of the square is the square root of its area. In this diagram, the square has an area of 16 units and a side length of 4 units.
These equations are both true: $$4^2=16$$ $$\sqrt{16}=4$$
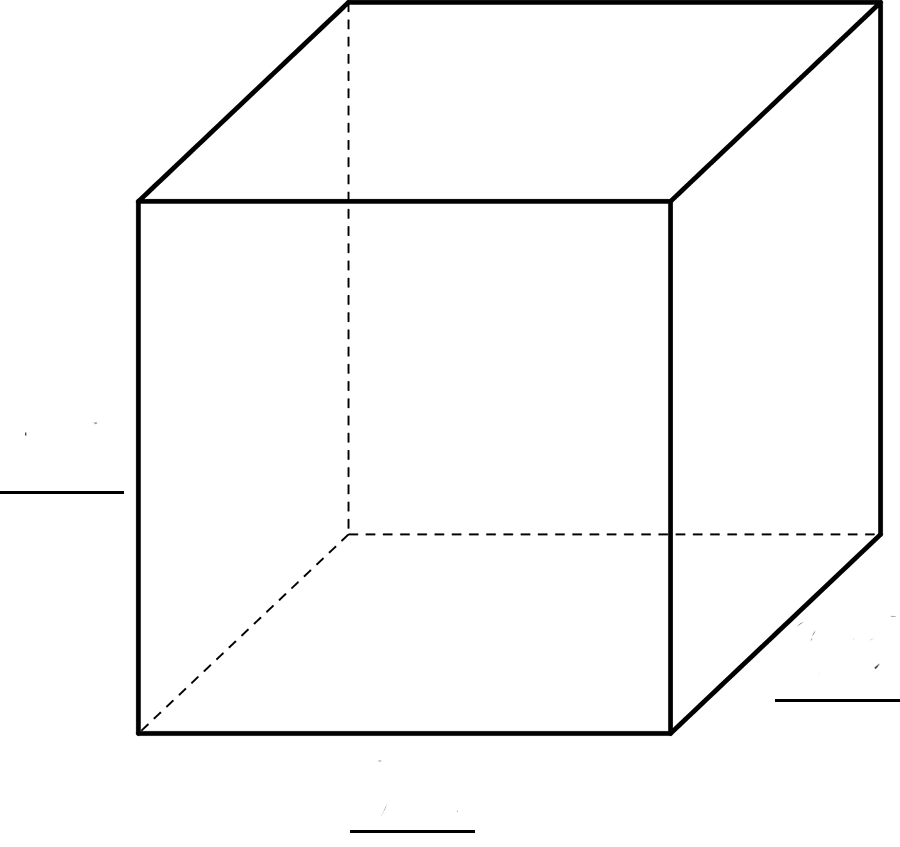
Now think about a solid cube. The cube has a volume, and the edge length of the cube is called the cube root of its volume. In this diagram, the cube has a volume of 64 units and an edge length of 4 units:
These equations are both true:
$$4^3=64$$
$$\sqrt[3]{64}=4$$
$\sqrt[3]{64}$ is pronounced “The cube root of 64.” Here are some other values of cube roots:
$\sqrt[3]{8}=2$, because $2^3=8$
$\sqrt[3]{27}=3$, because $3^3=27$
$\sqrt[3]{125}=5$, because $5^3=125$