2.1: Notice and Wonder: Polygon Patterns
What do you notice? What do you wonder?

Let’s explore geometric patterns!
What do you notice? What do you wonder?

Select the shape tool by clicking on it. Create copies of your shape by clicking in the work space.
When you have enough to work with, click on the Move tool (the arrow) to drag or turn them.
If you have trouble aligning the shapes, right click to turn on the grid.
When you are finished making your tessellation, you can hide the points.
Compare your tessellation to your partner’s. How are they similar? How are they different?
If possible, make a third tessellation of the plane with your shape (different from the ones you and your partner already created). If not possible, explain why it is not possible.
Pick one of the figures and describe the tessellation. Your partner will identify which tessellation you are describing. Then trade roles so your partner describes the tessellation and you identify the figure.

You and your partner each have a card with a tessellation. Describe what is on your card so that your partner can produce the tessellation (this should be done so that you cannot see your partner’s work until it is complete).
Check together to see if your partner’s tessellation agrees with your card and discuss any differences.
Change roles so your partner describes a tessellation, which you attempt to produce.
For each shape (triangle, square, pentagon, hexagon, and octagon), decide if you can use that shape to make a regular tessellation of the plane. Explain your reasoning.
Can you make a regular tessellation of the plane using regular polygons with 7 sides? What about 9 sides? 10 sides? 11 sides? 12 sides? Explain.
How does the measure of each angle in a square compare to the measure of each angle in an equilateral triangle? How does the measure of each angle in a regular 8-sided polygon compare to the measure of each angle in a regular 7-sided polygon?
What happens to the angles in a regular polygon as you add more sides?
Which polygons can be used to make regular tessellations of the plane?
Your teacher will assign you one of the three triangles. Your goal is to find a tessellation of the plane with copies of the triangle.

Can you tessellate the plane with copies of the pentagon? Explain. Note that the two sides making angle A are congruent.
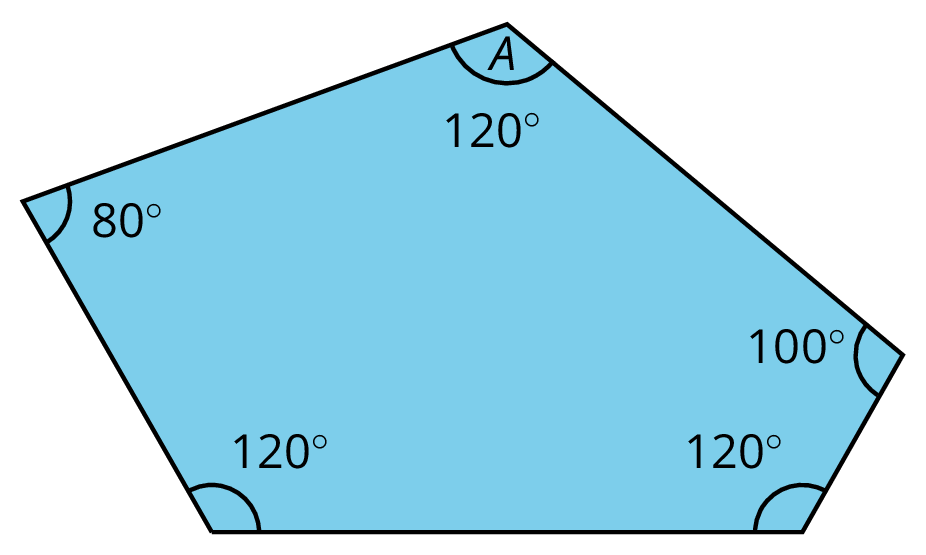
Pause your work here.
Take one pentagon and rotate it 120 degrees clockwise about the vertex at angle A, and trace the new pentagon. Next, rotate the pentagon 240 degrees clockwise about the vertex at angle A, and trace the new pentagon.
Explain why the three pentagons make a full circle at the central vertex.
A tessellation of the plane is a regular repeating pattern of one or more shapes that covers the entire plane.
