14.1: A Cylinder of Unknown Height
What is a possible volume for this cylinder if the diameter is 8 cm? Explain your reasoning.
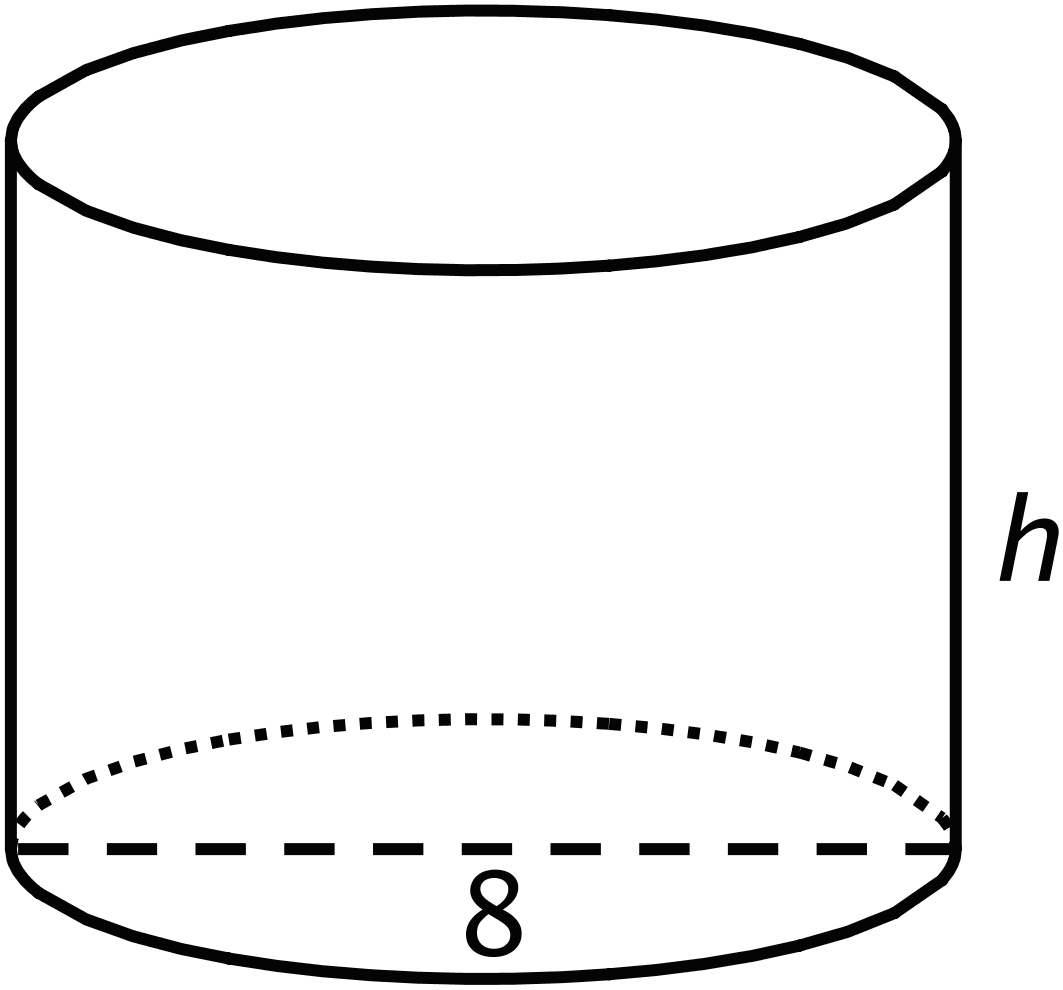
Let’s figure out the dimensions of cylinders.
What is a possible volume for this cylinder if the diameter is 8 cm? Explain your reasoning.

The volume V of a cylinder with radius r is given by the formula V=\pi r^2h.
50\pi = 5^2 \pi h
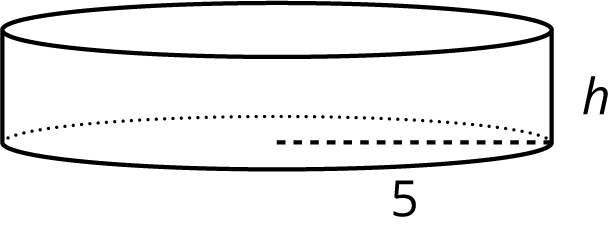
What does the height of this cylinder have to be? Explain how you know.
36\pi = r^2 \pi 4
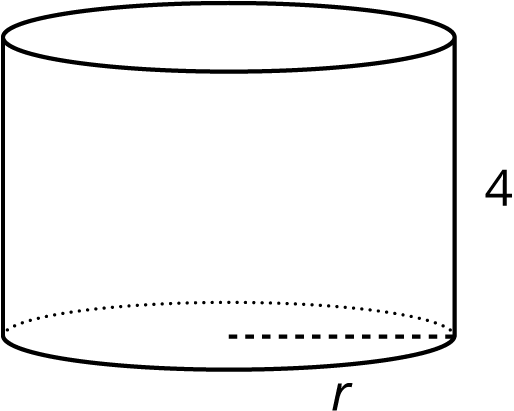
What does the radius of this cylinder have to be? Explain how you know.
Suppose a cylinder has a volume of 36\pi cubic inches, but it is not the same cylinder as the one you found earlier in this activity.
Each row of the table has information about a particular cylinder. Complete the table with the missing dimensions.
| diameter (units) | radius (units) | area of the base (square units) | height (units) | volume (cubic units) | |
|---|---|---|---|---|---|
| row 1 | 3 | 5 | |||
| row 2 | 12 | 108\pi | |||
| row 3 | 11 | 99\pi | |||
| row 4 | 8 | 16\pi | |||
| row 5 | 100 | 16\pi | |||
| row 6 | 10 | 20\pi | |||
| row 7 | 20 | 314 | |||
| row 8 | b | \pi \boldcdot b\boldcdot a^2 |
In an earlier lesson we learned that the volume, V, of a cylinder with radius r and height h is
V=\pi r^2 h
We say that the volume depends on the radius and height, and if we know the radius and height, we can find the volume. It is also true that if we know the volume and one dimension (either radius or height), we can find the other dimension.
For example, imagine a cylinder that has a volume of 500\pi cm3 and a radius of 5 cm, but the height is unknown. From the volume formula we know that
500\pi=\pi \boldcdot 25 \boldcdot h
must be true. Looking at the structure of the equation, we can see that 500 = 25h. That means that the height has to be 20 cm, since 500\div 25 = 20.
Now imagine another cylinder that also has a volume of 500\pi cm3 with an unknown radius and a height of 5 cm. Then we know that
500\pi=\pi\boldcdot r^2\boldcdot 5
must be true. Looking at the structure of this equation, we can see that r^2 = 100. So the radius must be 10 cm.