4.1: Diagonals

- What is the exact length of the line segment?
-
Find a decimal approximation of the length.
Let’s explore square roots.


Diego said that he thinks that $\sqrt{3}\approx 2.5$.

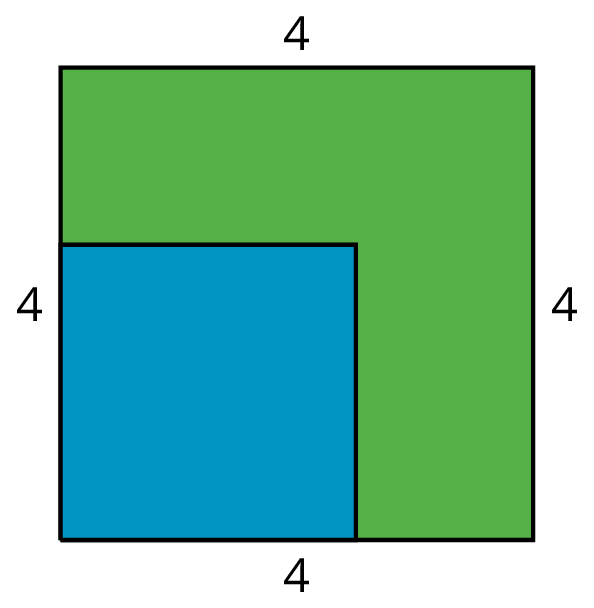
A farmer has a grassy patch of land enclosed by a fence in the shape of a square with a side length of 4 meters. To make it a suitable home for some animals, the farmer would like to carve out a smaller square to be filled with water, as in the figure.
What should the side length of the smaller square be so that half of the area is grass and half is water?
Here is a line segment on a grid. What is the length of this line segment?

By drawing some circles, we can tell that it’s longer than 2 units, but shorter than 3 units.

To find an exact value for the length of the segment, we can build a square on it, using the segment as one of the sides of the square.
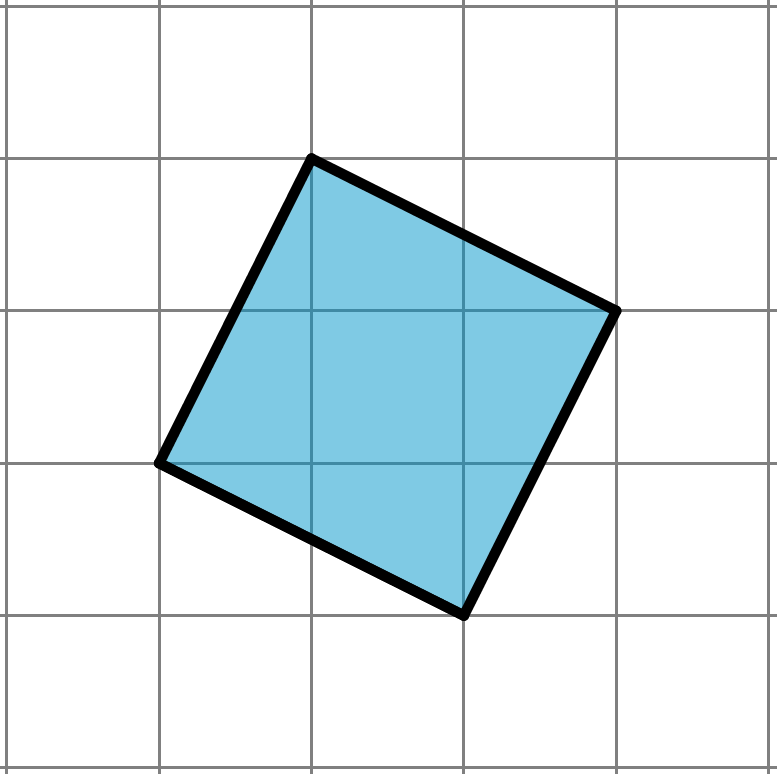
The area of this square is 5 square units. (Can you see why?) That means the exact value of the length of its side is $\sqrt5$ units.
Notice that 5 is greater than 4, but less than 9. That means that $\sqrt5$ is greater than 2, but less than 3. This makes sense because we already saw that the length of the segment is in between 2 and 3.
With some arithmetic, we can get an even more precise idea of where $\sqrt5$ is on the number line. The image with the circles shows that $\sqrt5$ is closer to 2 than 3, so let’s find the value of 2.12 and 2.22 and see how close they are to 5. It turns out that $2.1^2=4.41$ and $2.2^2=4.84$, so we need to try a larger number. If we increase our search by a tenth, we find that $2.3^2=5.29$. This means that $\sqrt5$ is greater than 2.2, but less than 2.3. If we wanted to keep going, we could try $2.25^2$ and eventually narrow the value of $\sqrt5$ to the hundredths place. Calculators do this same process to many decimal places, giving an approximation like $\sqrt5 \approx 2.2360679775$. Even though this is a lot of decimal places, it is still not exact because $\sqrt5$ is irrational.