8.1: Equivalent Expressions
Create three different expressions that are each equal to 20. Each expression should include only these three numbers: 4, \text- 2, and 10.
Let’s look at similar triangles.
Create three different expressions that are each equal to 20. Each expression should include only these three numbers: 4, \text- 2, and 10.
Your teacher will give you some dried pasta and a set of angles.
Find two others in the room who have the same angle A and compare your triangles. What is the same? What is different? Are the triangles congruent? Similar?
Find two others in the room who used your same angles and compare your triangles. What is the same? What is different? Are the triangles congruent? Similar?
How did you decide if they were or were not congruent or similar?
Here is triangle PQR. Break a new piece of pasta, different in length than segment PQ.
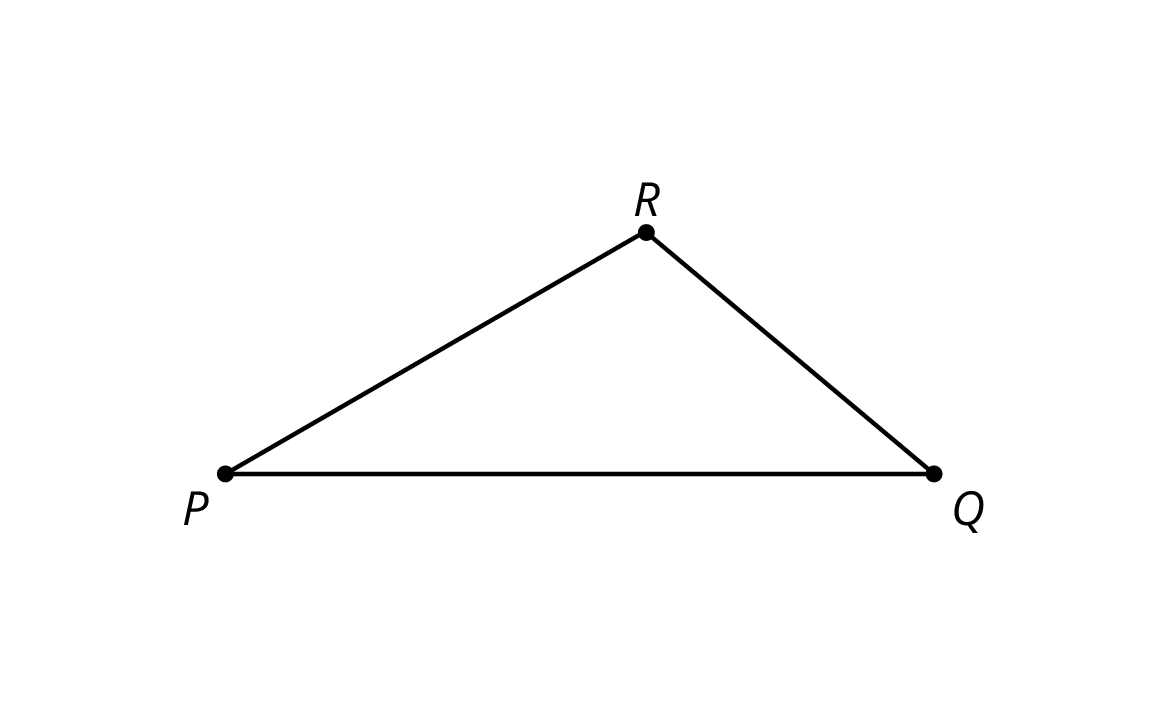
Is your new pasta triangle PST similar to \triangle PQR? Explain your reasoning.
If your broken piece of pasta were a different length, would the pasta triangle still be similar to \triangle PQR? Explain your reasoning.
Quadrilaterals ABCD and EFGH have four angles measuring 240^\circ, 40^\circ, 40^\circ, and 40^\circ. Do ABCD and EFGH have to be similar?
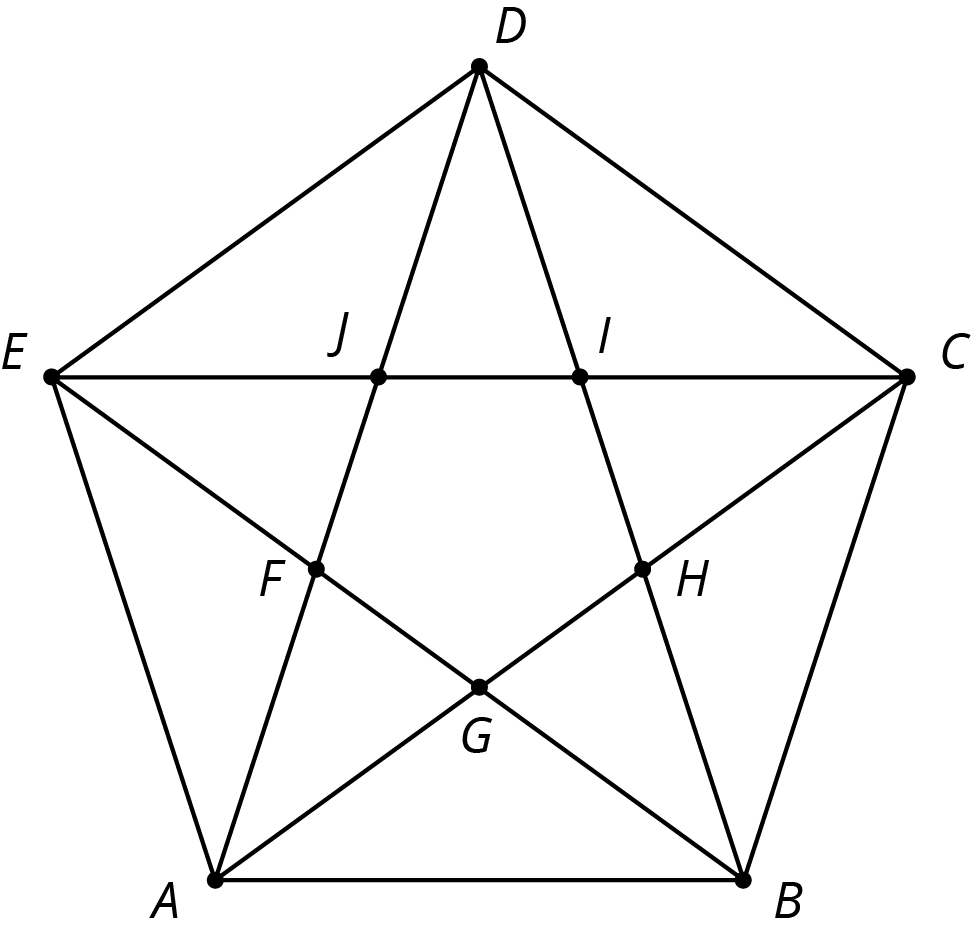
This diagram has several triangles that are similar to triangle DJI.
We learned earlier that two polygons are similar when there is a sequence of translations, rotations, reflections, and dilations taking one polygon to the other. When the polygons are triangles, we only need to check that that both triangles have two corresponding angles to show they are similar—can you tell why?
Here is an example. Triangle ABC and triangle DEF each have a 30 degree angle and a 45 degree angle.
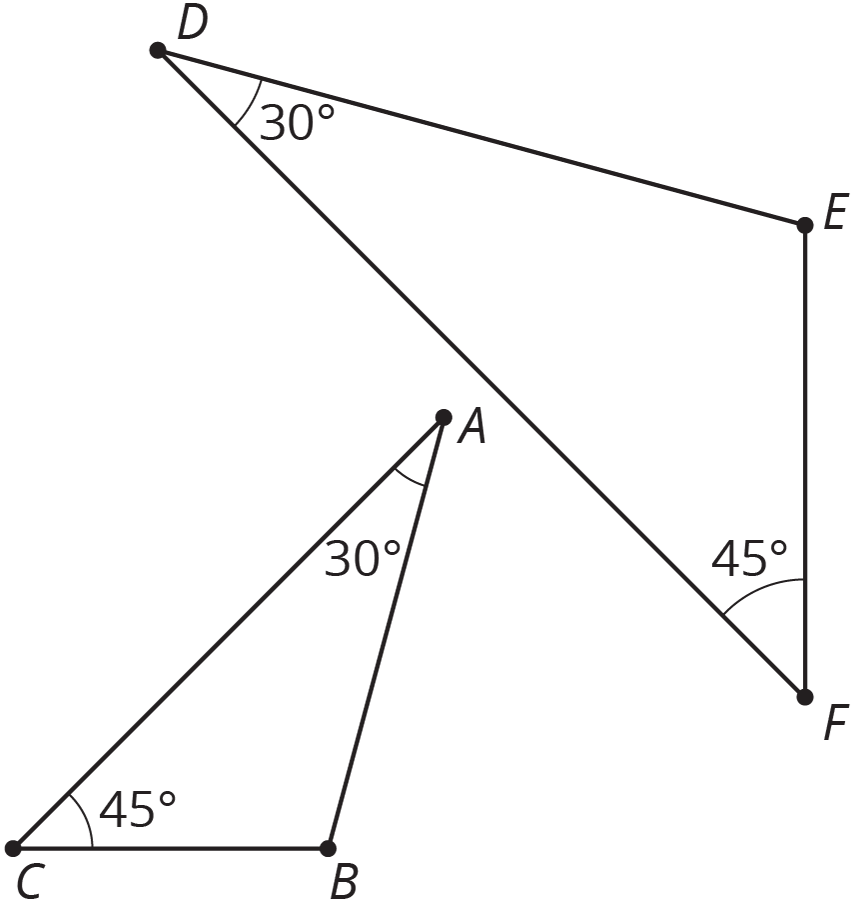
We can translate A to D and then rotate so that the two 30 degree angles are aligned, giving this picture:
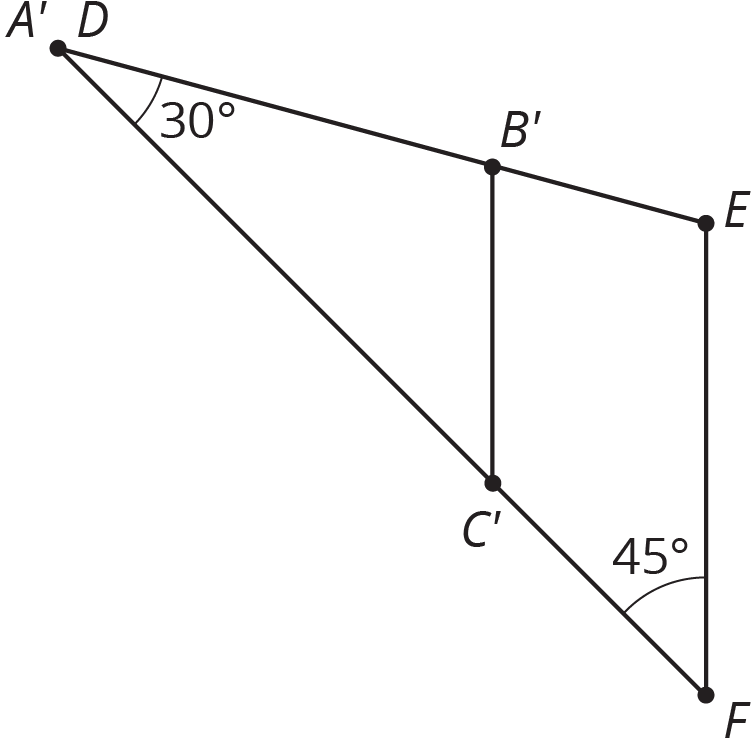 Now a dilation with center D and appropriate scale factor will move C' to F. This dilation also moves B' to E, showing that triangles ABC and DEF are similar.
Now a dilation with center D and appropriate scale factor will move C' to F. This dilation also moves B' to E, showing that triangles ABC and DEF are similar.