- Plot a point on Circle c. Label the point P. Plot where P goes when the dilation is applied.
- Plot a point on Circle d. Label the point Q. Plot a point that the dilation takes to Q.
Unit 2: Practice Problem Sets
Lesson 1
Problem 1
Rectangle A measures 12 cm by 3 cm. Rectangle B is a scaled copy of Rectangle A. Select all of the measurement pairs that could be the dimensions of Rectangle B.
- 6 cm by 1.5 cm
- 10 cm by 2 cm
- 13 cm by 4 cm
- 18 cm by 4.5 cm
- 80 cm by 20 cm
Problem 2
Rectangle A has length 12 and width 8. Rectangle B has length 15 and width 10. Rectangle C has length 30 and width 15.
- Is Rectangle A a scaled copy of Rectangle B? If so, what is the scale factor?
- Is Rectangle B a scaled copy of Rectangle A? If so, what is the scale factor?
-
Explain how you know that Rectangle C is not a scaled copy of Rectangle B.
- Is Rectangle A a scaled copy of Rectangle C? If so, what is the scale factor?
Problem 3
Here are three polygons.
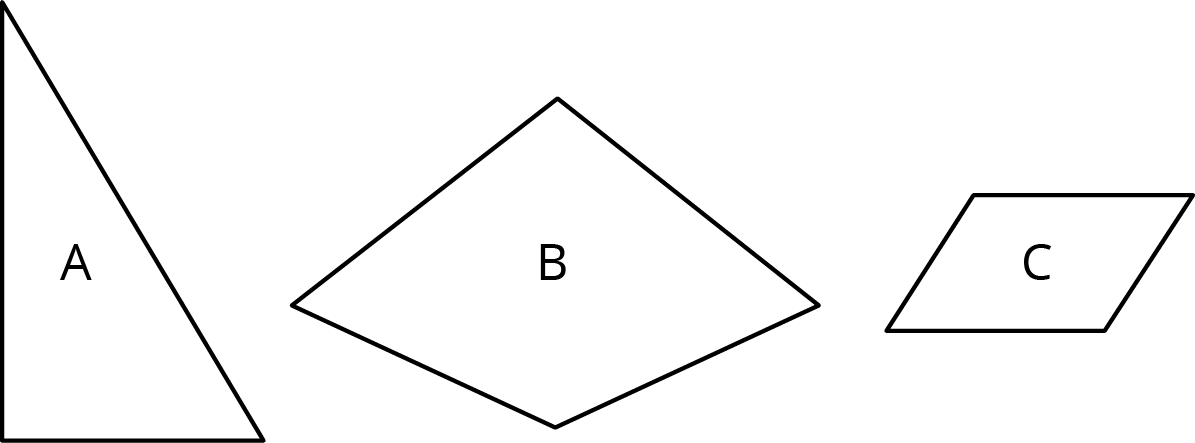
-
Draw a scaled copy of Polygon A with scale factor \frac 1 2.
-
Draw a scaled copy of Polygon B with scale factor 2.
-
Draw a scaled copy of Polygon C with scale factor \frac 1 4.
Problem 4 (from Unit 1, Lesson 15)
Which of these sets of angle measures could be the three angles in a triangle?
- 40^\circ, 50^\circ, 60^\circ
- 50^\circ, 60^\circ, 70^\circ
- 60^\circ, 70^\circ, 80^\circ
- 70^\circ, 80^\circ, 90^\circ
Problem 5 (from Unit 1, Lesson 14)
In the picture lines AB and CD are parallel. Find the measures of the following angles. Explain your reasoning.
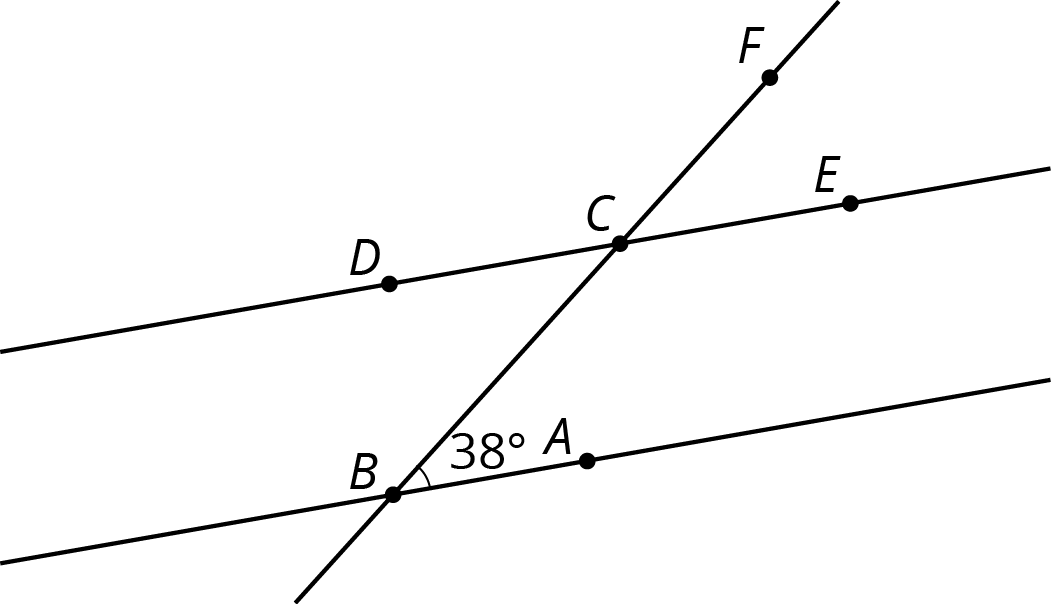
- \angle BCD
- \angle ECF
- \angle DCF
Lesson 2
Problem 1
Here are Circles c and d. Point O is the center of dilation, and the dilation takes Circle c to Circle d.

Problem 2
Here is triangle ABC.

- Dilate each vertex of triangle ABC using P as the center of dilation and a scale factor of 2. Draw the triangle connecting the three new points.
- Dilate each vertex of triangle ABC using P as the center of dilation and a scale factor of \frac 1 2. Draw the triangle connecting the three new points.
-
Measure the longest side of each of the three triangles. What do you notice?
-
Measure the angles of each triangle. What do you notice?
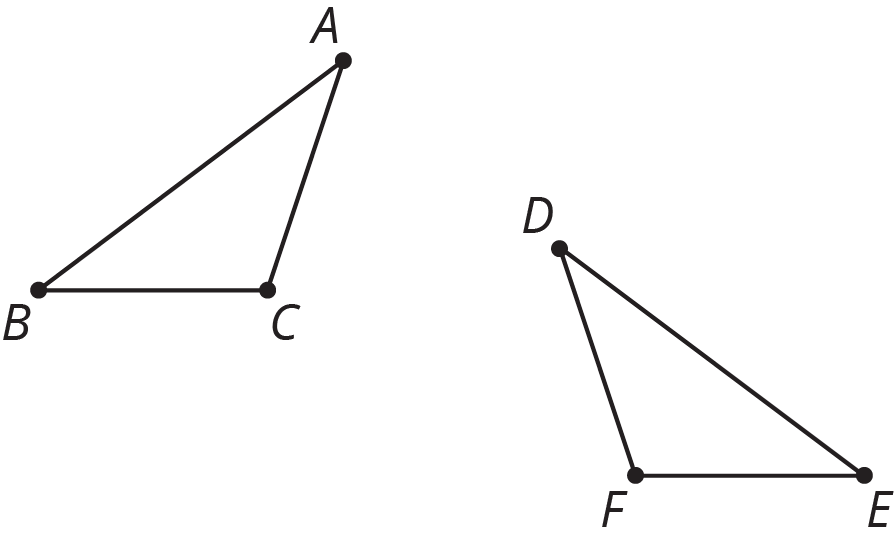
Problem 3 (from Unit 1, Lesson 12)
Describe a rigid transformation that you could use to show the polygons are congruent.
Problem 4 (from Unit 1, Lesson 15)
The line has been partitioned into three angles.

Is there a triangle with these three angle measures? Explain.
Lesson 3
Problem 1
Segment AB measures 3 cm. Point O is the center of dilation. How long is the image of AB after a dilation with . . .
- Scale factor 5?
- Scale factor 3.7?
- Scale factor \frac 1 5?
- Scale factor s?
Problem 2
Here are points A and B. Plot the points for each dilation described.

- C is the image of B using A as the center of dilation and a scale factor of 2.
- D is the image of A using B as the center of dilation and a scale factor of 2.
- E is the image of B using A as the center of dilation and a scale factor of \frac 1 2.
- F is the image of A using B as the center of dilation and a scale factor of \frac 1 2.
Problem 3
Problem 4 (from Unit 2, Lesson 1)
Triangle ABC is a scaled copy of triangle DEF. Side AB measures 12 cm and is the longest side of ABC. Side DE measures 8 cm and is the longest side of DEF.
- Triangle ABC is a scaled copy of triangle DEF with what scale factor?
- Triangle DEF is a scaled copy of triangle ABC with what scale factor?
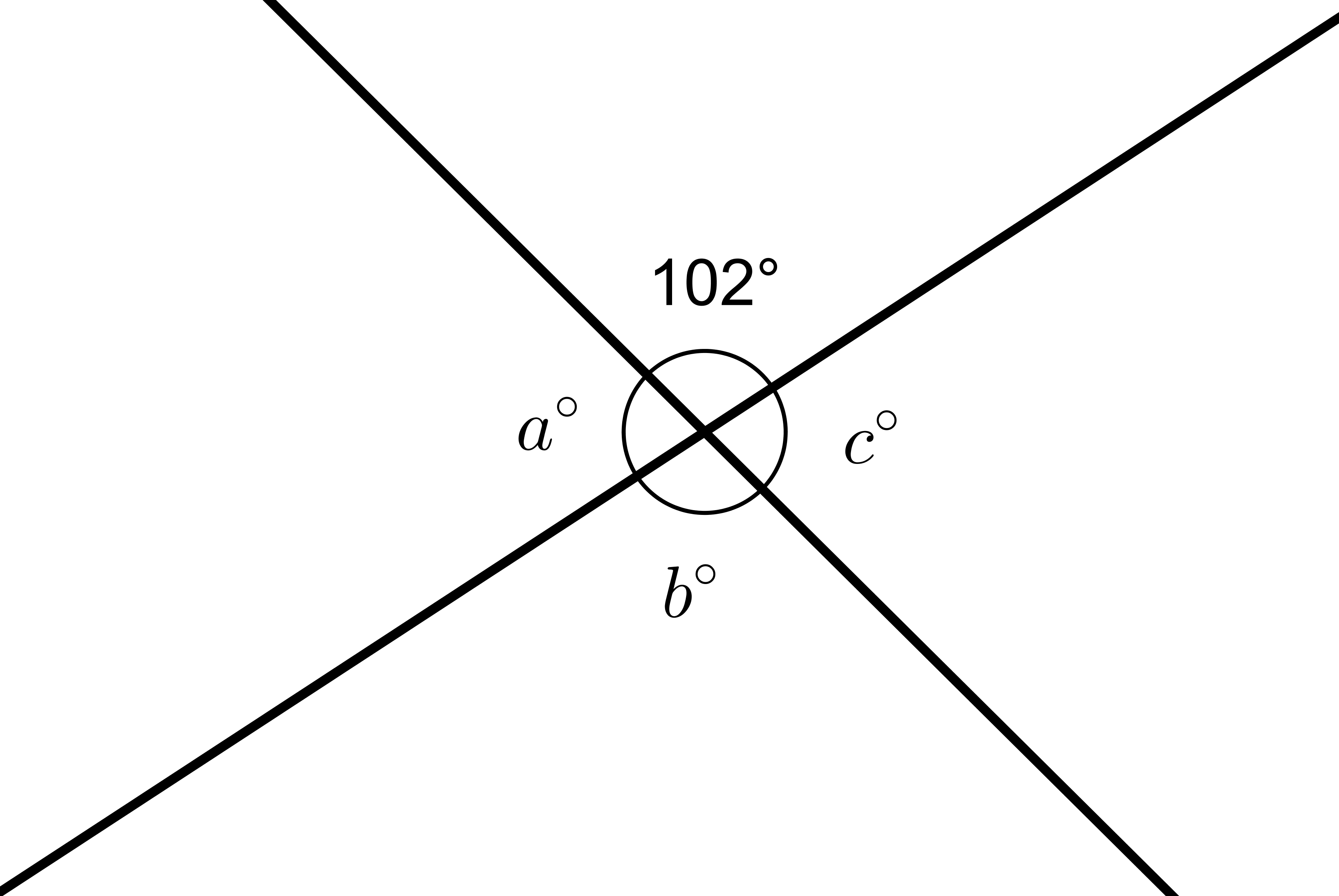
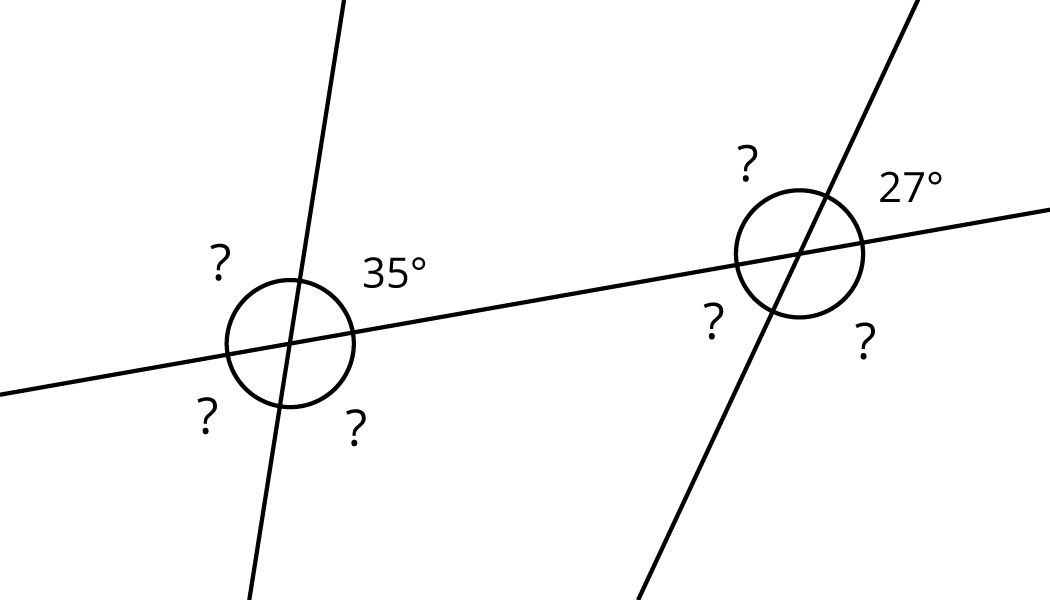
Problem 5 (from Unit 1, Lesson 14)
The diagram shows two intersecting lines.
Find the missing angle measures.
Problem 6 (from Unit 1, Lesson 12)
- Show that the two triangles are congruent.
- Find the side lengths of DEF and the angle measures of ABC.
Lesson 4
Problem 1
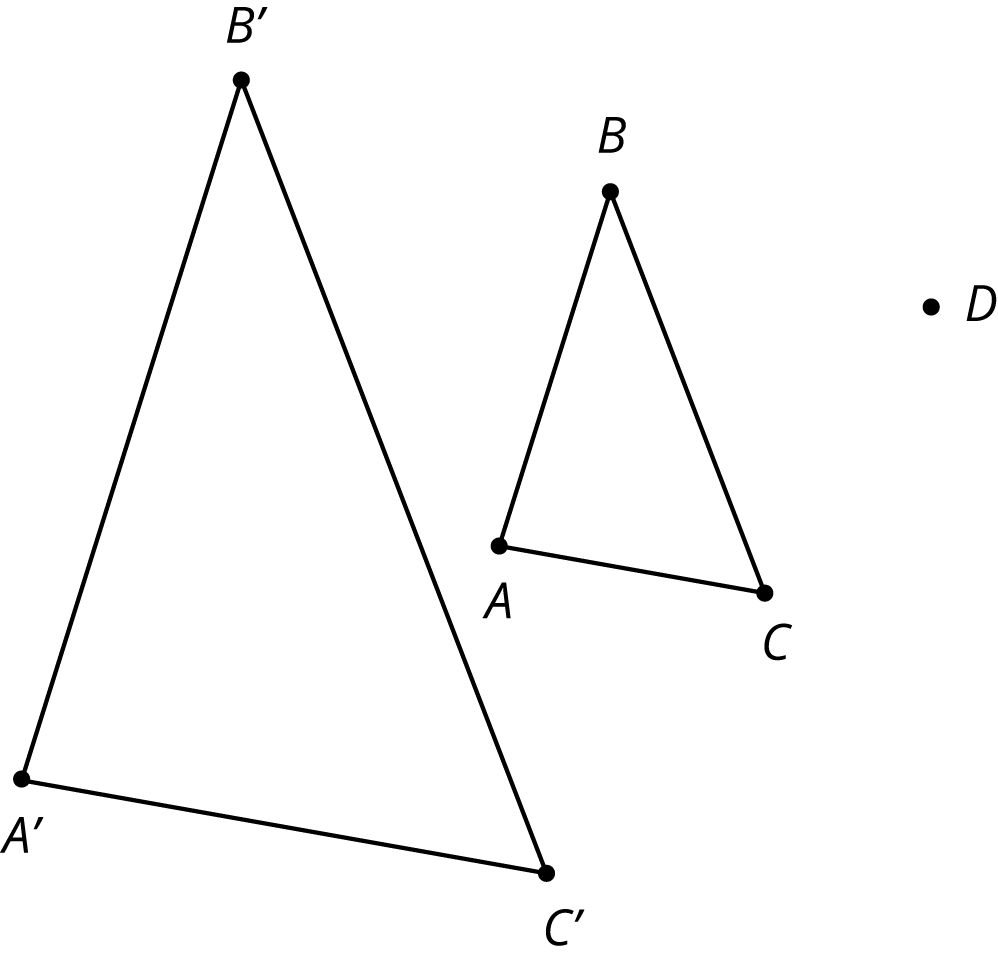
Triangle ABC is dilated using D as the center of dilation with scale factor 2.
The image is triangle A’B’C’. Clare says the two triangles are congruent, because their angle measures are the same. Do you agree? Explain how you know.
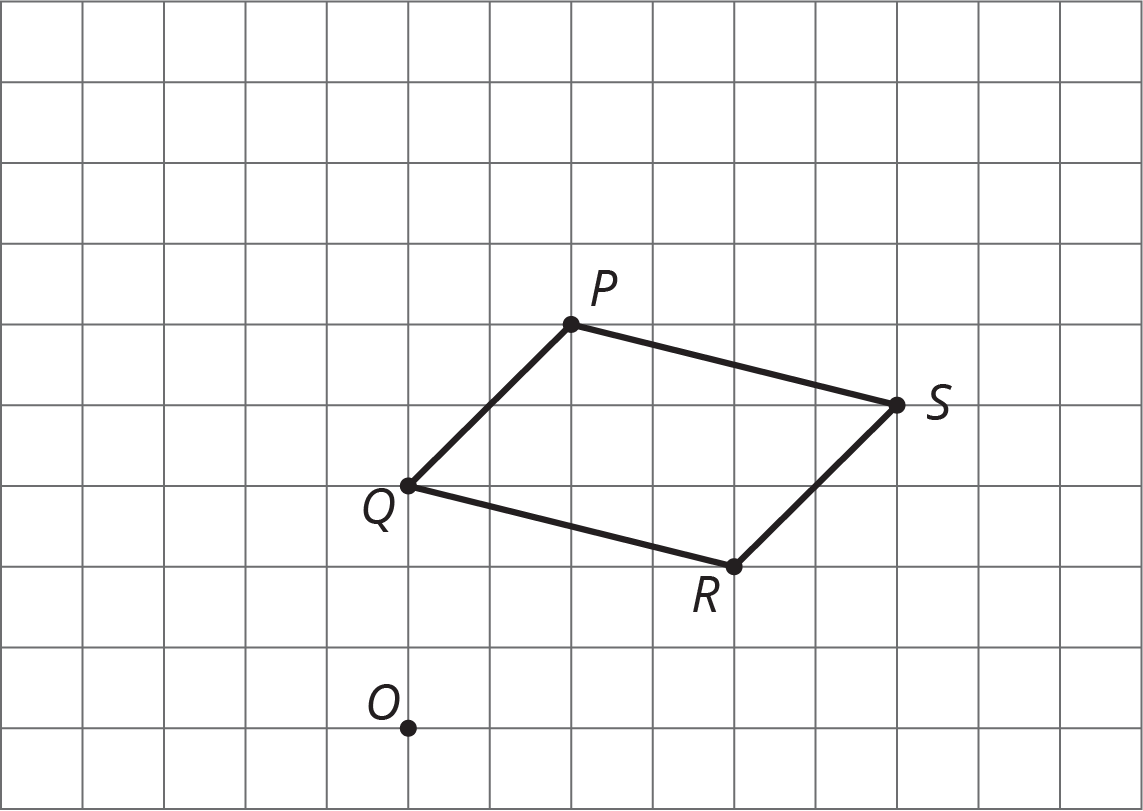
Problem 2
On graph paper, sketch the image of quadrilateral PQRS under the following dilations:
- The dilation centered at R with scale factor 2.
- The dilation centered at O with scale factor \frac{1}{2}.
- The dilation centered at S with scale factor \frac{1}{2}.
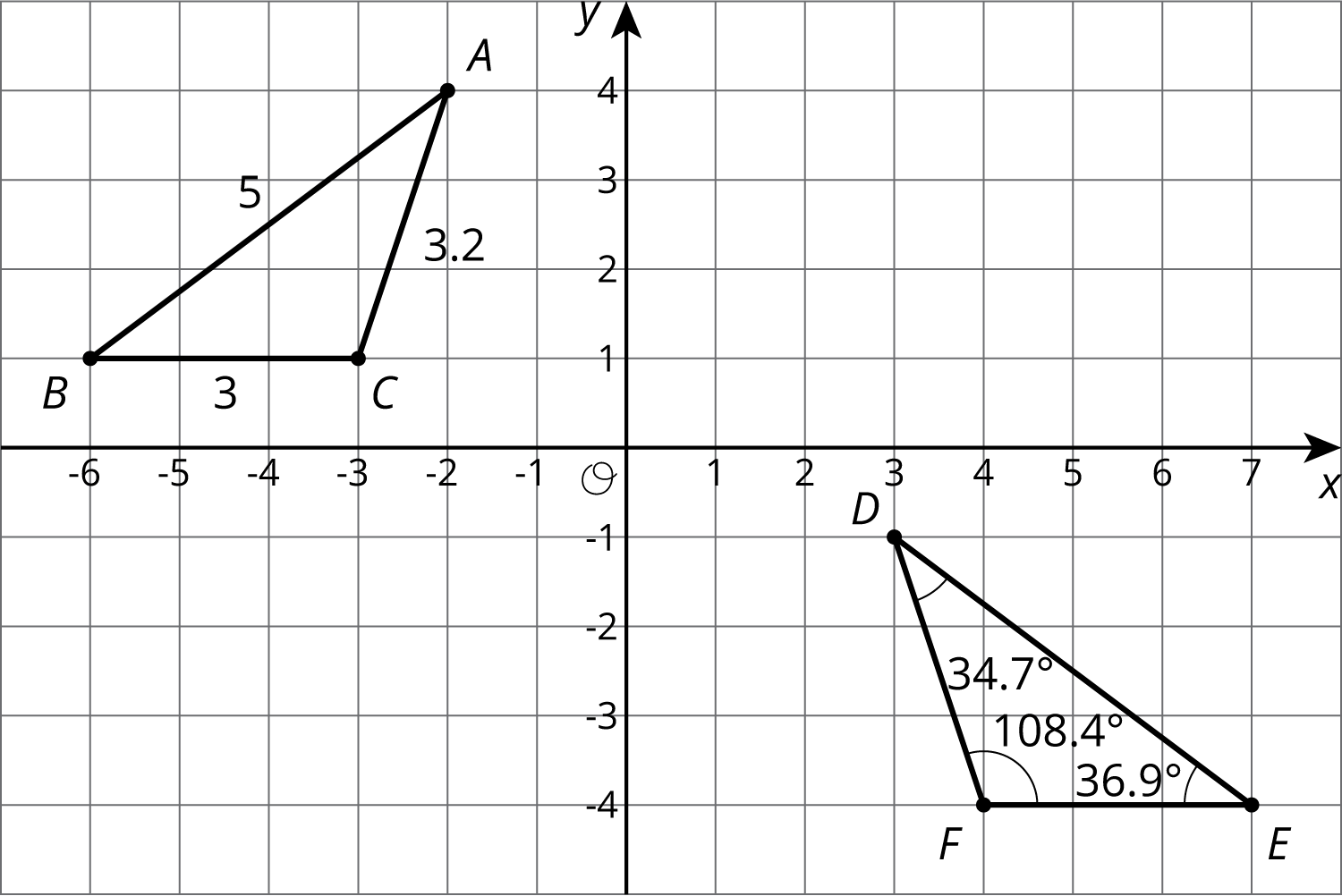
Problem 3 (from Unit 1, Lesson 14)
The diagram shows three lines with some marked angle measures.
Find the missing angle measures marked with question marks.
Problem 4 (from Unit 1, Lesson 4)
Describe a sequence of translations, rotations, and reflections that takes Polygon P to Polygon Q.

Problem 5 (from Unit 1, Lesson 6)
Point B has coordinates (\text-2,\text-5). After a translation 4 units down, a reflection across the y-axis, and a translation 6 units up, what are the coordinates of the image?
Lesson 5
Problem 1
Quadrilateral ABCD is dilated with center (0,0), taking B to B'. Draw A'B'C'D'.
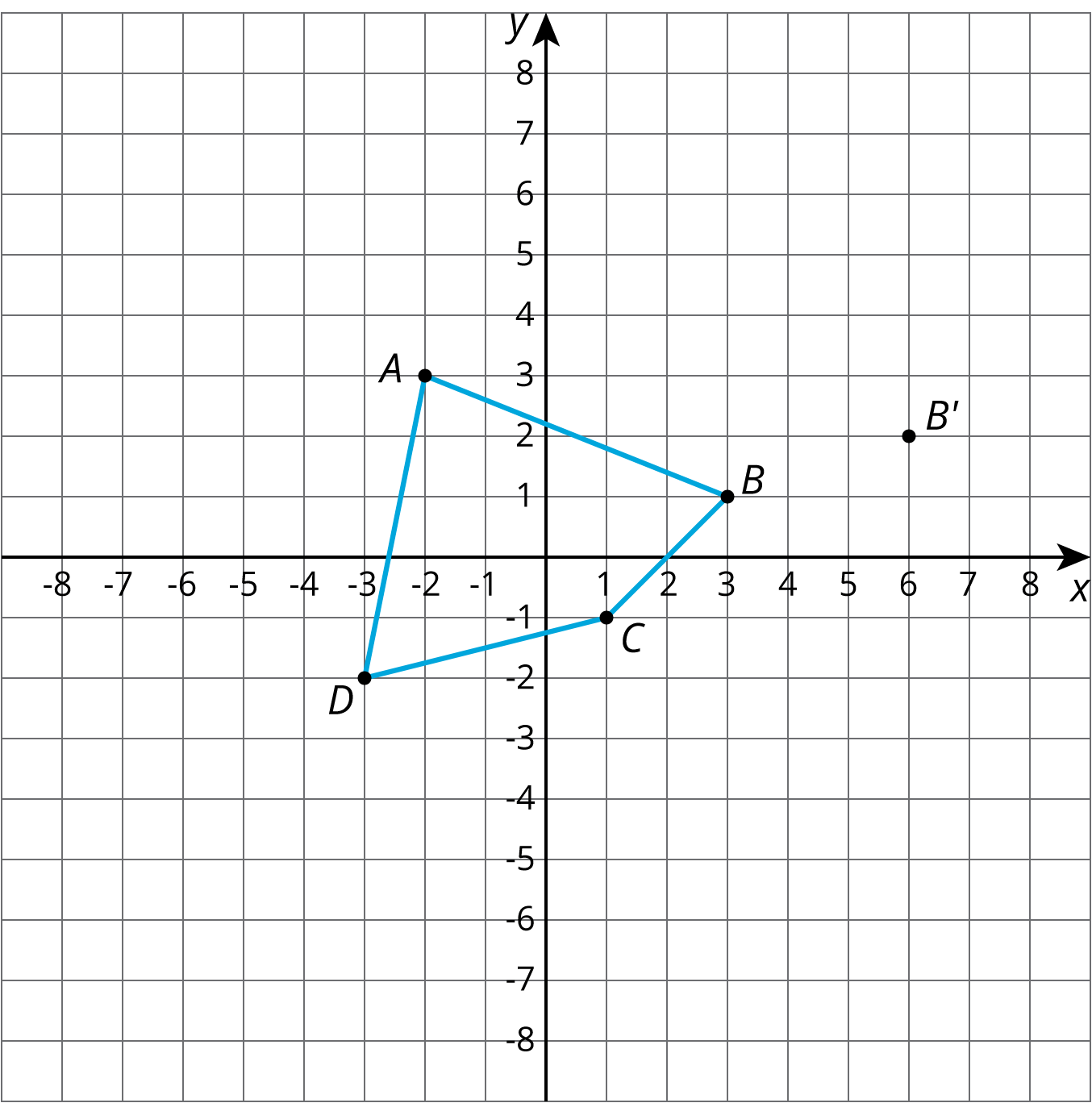
Problem 2
Triangles B and C have been built by dilating Triangle A.
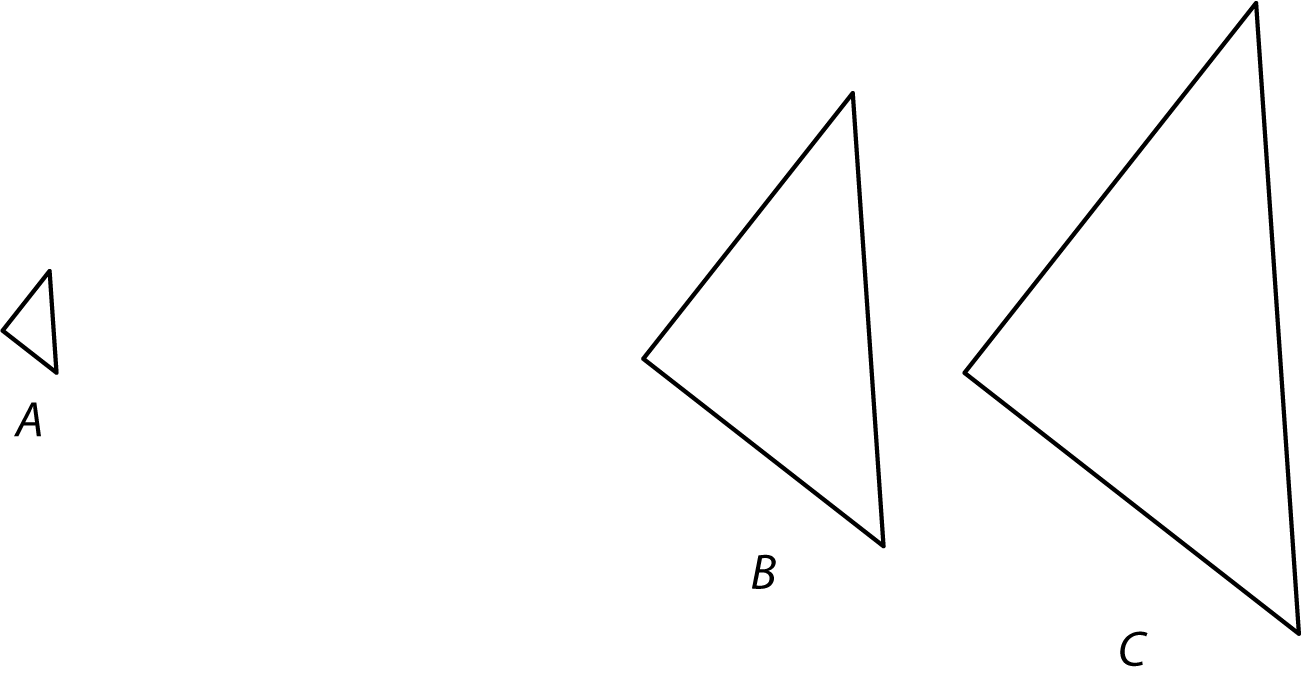
- Find the center of dilation.
- Triangle B is a dilation of A with approximately what scale factor?
- Triangle A is a dilation of B with approximately what scale factor?
- Triangle B is a dilation of C with approximately what scale factor?
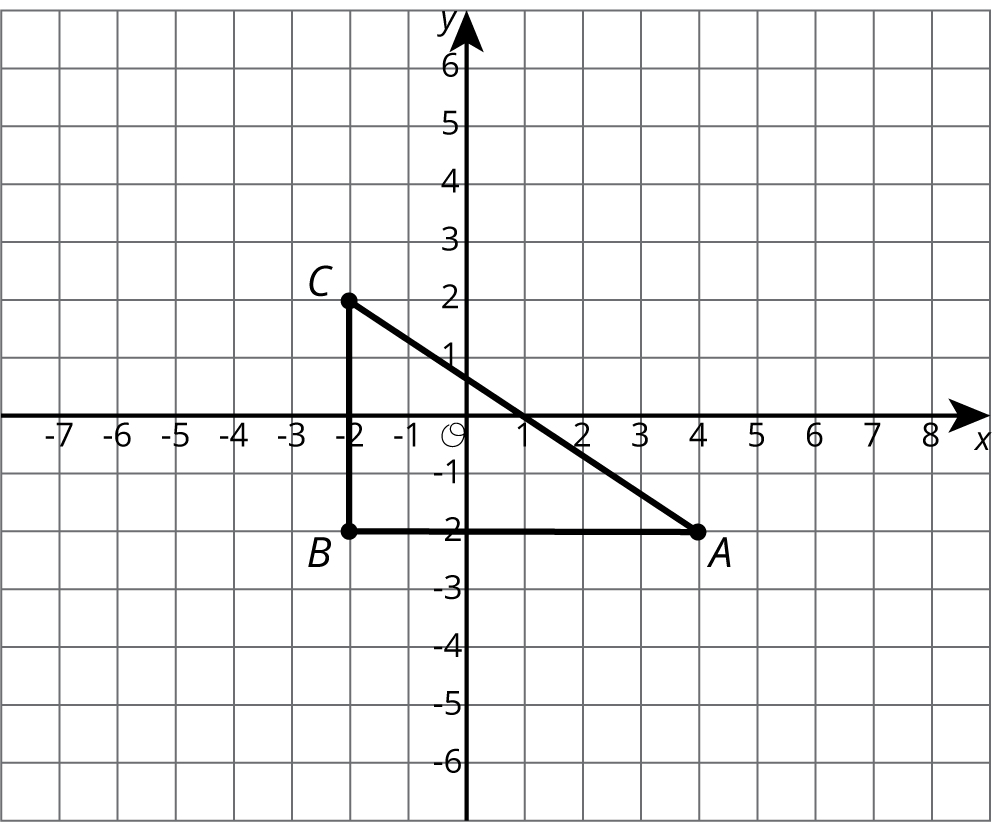
Problem 3
Here is a triangle.
- Draw the dilation of triangle ABC, with center (0,0), and scale factor 2. Label this triangle A’B’C’.
- Draw the dilation of triangle ABC, with center (0,0), and scale factor \frac{1}{2}. Label this triangle A’’B’’C’’.
- Is A’’B’’C’’ a dilation of triangle A’B’C’? If yes, what are the center of dilation and the scale factor?
Problem 4 (from Unit 1, Lesson 15)
Triangle ABC is a right triangle, and the measure of angle A is 28^\circ. What are the measures of the other two angles?
Lesson 6
Problem 1
Each diagram has a pair of figures, one larger than the other. For each pair, show that the two figures are similar by identifying a sequence of translations, rotations, reflections, and dilations that takes the smaller figure to the larger one.

Problem 2
Here are two similar polygons.
Measure the side lengths and angles of each polygon. What do you notice?

Problem 3
Each figure shows a pair of similar triangles, one contained in the other. For each pair, describe a point and a scale factor to use for a dilation moving the larger triangle to the smaller one. Use a measurement tool to find the scale factor.
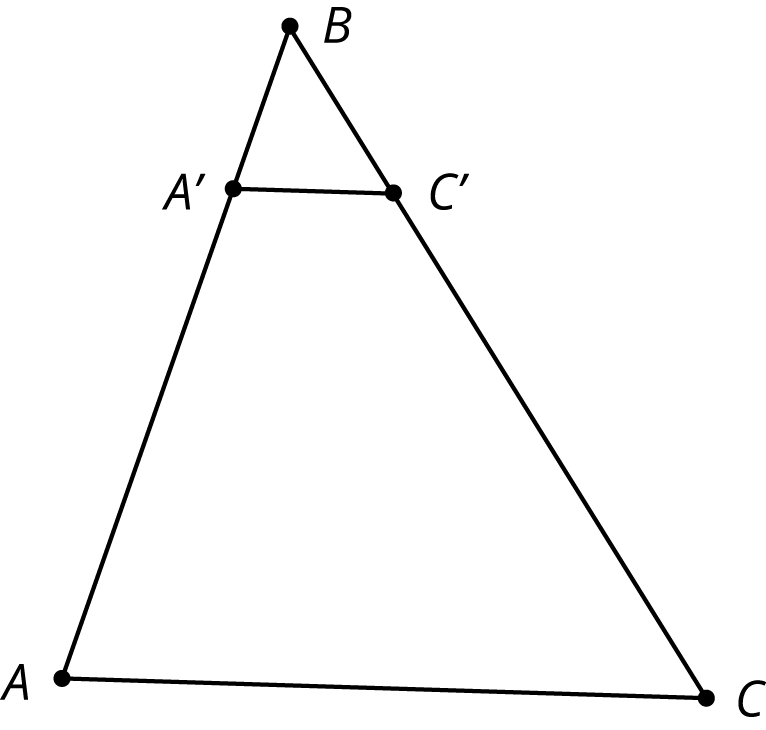
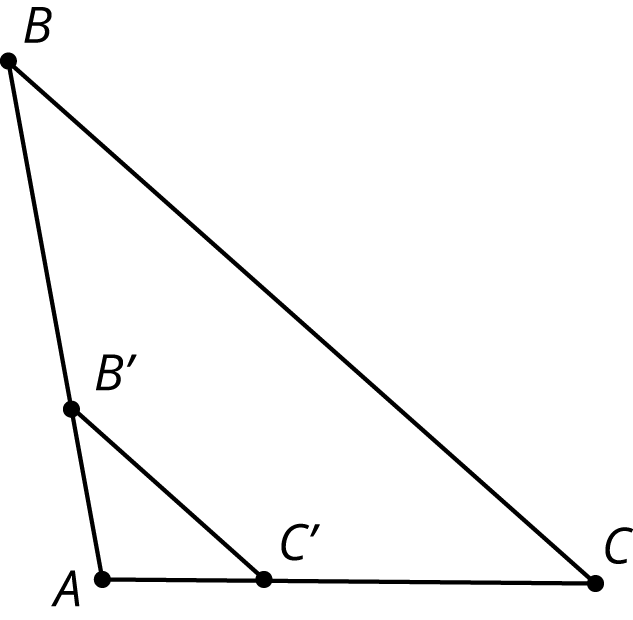
Lesson 7
Problem 1
Triangle DEF is a dilation of triangle ABC with scale factor 2. In triangle ABC, the largest angle measures 82^\circ. What is the largest angle measure in triangle DEF?
- 41^\circ
- 82^\circ
- 123^\circ
- 164^\circ
Problem 2
Draw two polygons that are similar but could be mistaken for not being similar. Explain why they are similar.
Problem 3
Draw two polygons that are not similar but could be mistaken for being similar. Explain why they are not similar.
Problem 4
These two triangles are similar. Find side lengths a and b. Note: the two figures are not drawn to scale.

Problem 5 (from Unit 2, Lesson 3)
Jada claims that B’C’D’ is a dilation of BCD using A as the center of dilation.
What are some ways you can convince Jada that her claim is not true?
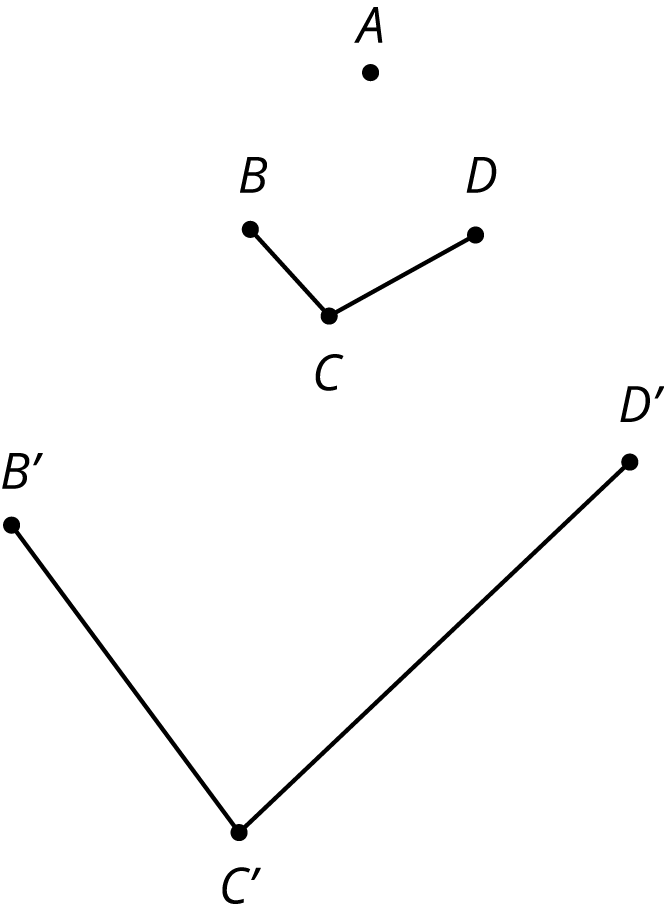
Problem 6 (from Unit 1, Lesson 8)
- Draw a horizontal line segment AB.
- Rotate segment AB 90^\circ counterclockwise around point A. Label any new points.
- Rotate segment AB 90^\circ clockwise around point B. Label any new points.
- Describe a transformation on segment AB you could use to finish building a square.
Lesson 8
Problem 1
In each pair, some of the angles of two triangles in degrees are given. Use the information to decide if the triangles are similar or not. Explain how you know.
-
Triangle A: 53, 71, ___; Triangle B: 53, 71, ___
-
Triangle C: 90, 37, ___; Triangle D: 90, 53, ___
-
Triangle E: 63, 45, ____; Triangle F: 14, 71, ____
-
Triangle G: 121, ___, ___; Triangle H: 70, ___, ___
Problem 2
-
Draw two equilateral triangles that are not congruent.
- Measure the side lengths and angles of your triangles. Are the two triangles similar?
-
Do you think two equilateral triangles will be similar always, sometimes, or never? Explain your reasoning.
Problem 3
In the figure, line BC is parallel to line DE.

Explain why \triangle ABC is similar to \triangle ADE.
Problem 4 (from Unit 2, Lesson 4)
The quadrilateral PQRS in the diagram is a parallelogram. Let P’Q’R’S’ be the image of PQRS after applying a dilation centered at a point O (not shown) with scale factor 3.
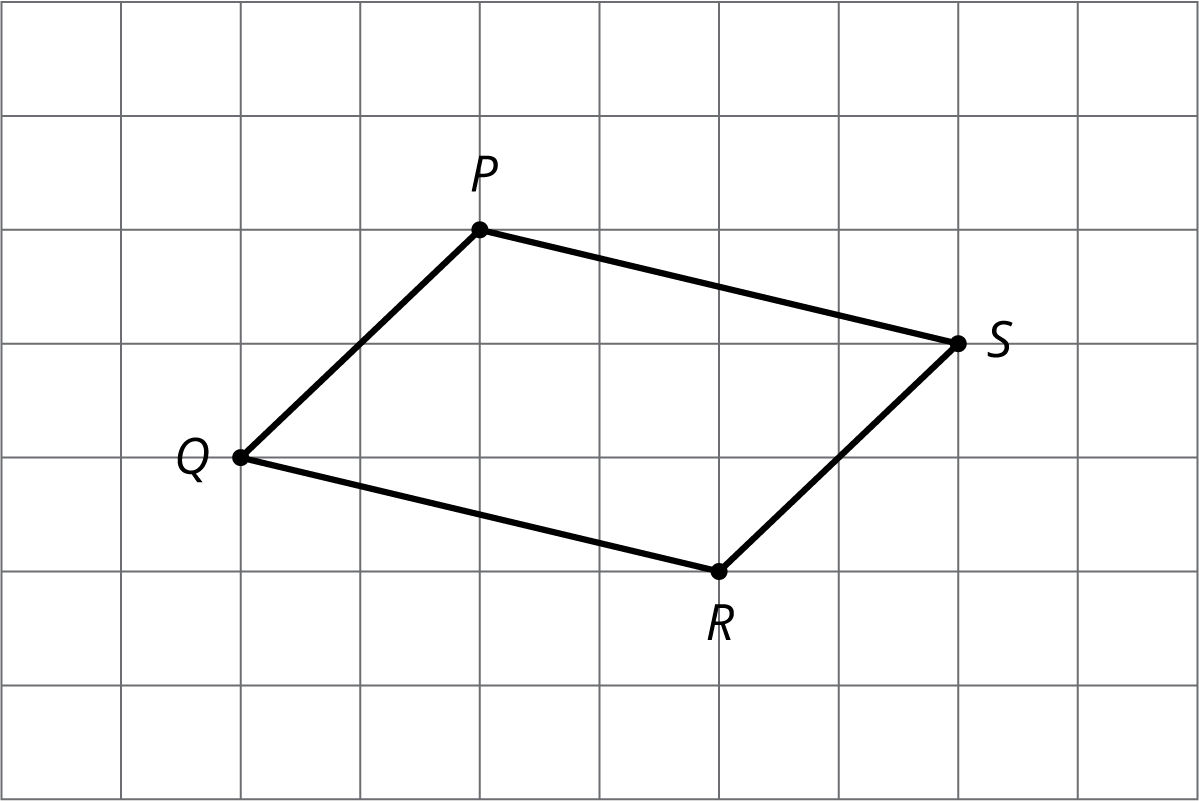
Which of the following is true?
- P’Q’= PQ
- P’Q’=3PQ
- PQ=3P’Q’
- Cannot be determined from the information given
Problem 5 (from Unit 1, Lesson 6)
Describe a sequence of transformations for which Quadrilateral P is the image of Quadrilateral Q.

Lesson 9
Problem 1
These two triangles are similar.
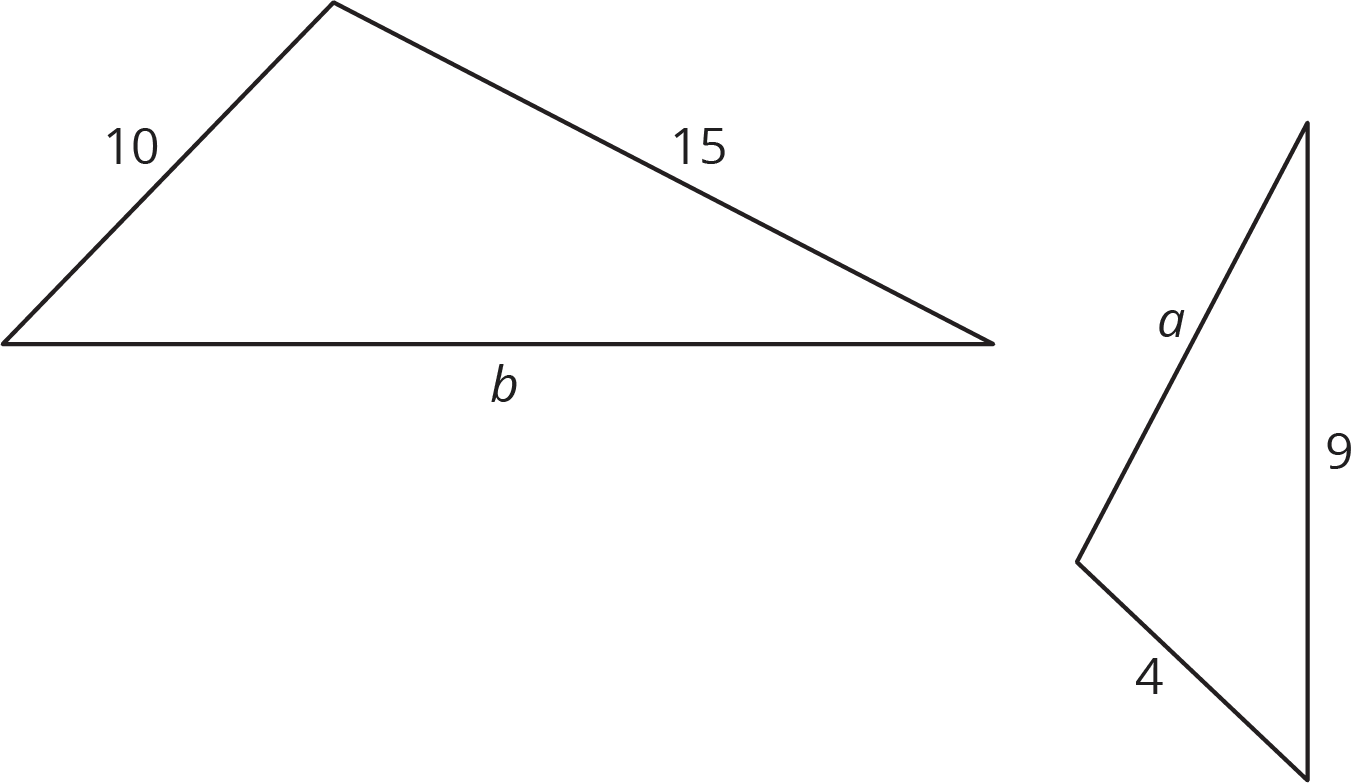
What are a and b? Note: the two figures are not drawn to scale.
Problem 2
Here is triangle ABC. Triangle XYZ is similar to ABC with scale factor \frac 1 4.
- Draw what triangle XYZ might look like.
-
How do the angle measures of triangle XYZ compare to triangle ABC? Explain how you know.
-
What are the side lengths of triangle XYZ?
- For triangle XYZ, calculate (long side) \div (medium side), and compare to triangle ABC.
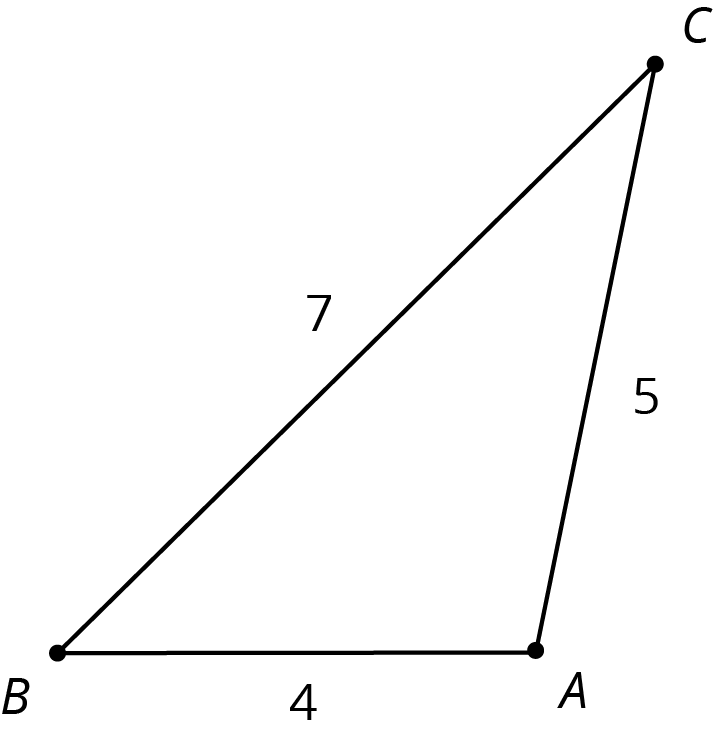
Problem 3
The two triangles shown are similar. Find the value of \frac d c.

Problem 4 (from Unit 2, Lesson 5)
The diagram shows two nested triangles that share a vertex. Find a center and a scale factor for a dilation that would move the larger triangle to the smaller triangle.

Lesson 10
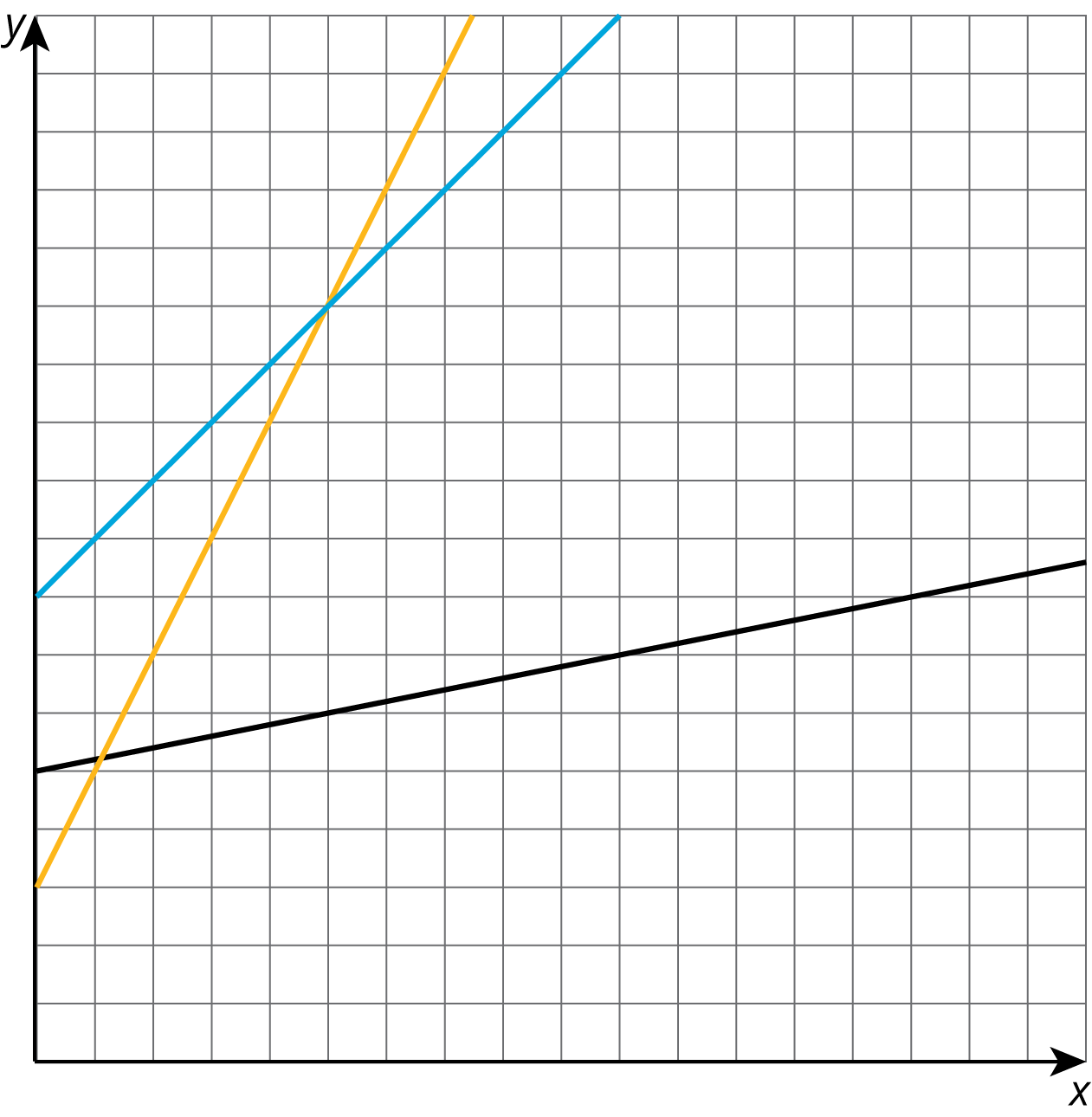
Problem 1
Of the three lines in the graph, one has slope 1, one has slope 2, and one has slope \frac{1}{5}. Label each line with its slope.
Problem 2
Draw three lines with slope 2, and three lines with slope \frac 1 3. What do you notice?

Problem 3
The figure shows two right triangles, each with its longest side on the same line.

- Explain how you know the two triangles are similar.
- How long is XY?
- For each triangle, calculate (vertical side) \div (horizontal side).
- What is the slope of the line? Explain how you know.
Problem 4 (from Unit 2, Lesson 9)
Triangle A has side lengths 3, 4, and 5. Triangle B has side lengths 6, 7, and 8.
-
Explain how you know that Triangle B is not similar to Triangle A.
- Give possible side lengths for Triangle B so that it is similar to Triangle A.
Lesson 11
Problem 1
For each pair of points, find the slope of the line that passes through both points. If you get stuck, try plotting the points on graph paper and drawing the line through them with a ruler.
- (1,1) and (7,5)
- (1,1) and (5,7)
- (2,5) and (\text-1,2)
- (2,5) and (\text-7,\text-4)
Problem 2
Line \ell is shown in the coordinate plane.

- What are the coordinates of B and D?
- Is the point (16,20) on line \ell? Explain how you know.
- Is the point (20,24) on line \ell? Explain how you know.
- Is the point (80,100) on line \ell? Explain how you know.
- Write a rule that would allow you to test whether (x,y) is on line \ell.
Problem 3
Consider the graphed line.
Mai uses Triangle A and says the slope of this line is \frac{6}{4}. Elena uses Triangle B and says no, the slope of this line is 1.5. Do you agree with either of them? Explain.

Problem 4 (from Unit 2, Lesson 7)
A rectangle has length 6 and height 4.
Which of these would tell you that quadrilateral ABCD is definitely not similar to this rectangle? Select all that apply.
- AB=BC
- m{\angle ABC}=105^\circ
- AB=8
- BC=8
- BC=2 \boldcdot AB
- 2 \boldcdot AB=3 \boldcdot BC
Lesson 12
Problem 1
Select all the points that are on the line through (0,5) and (2,8).
- (4,11)
- (5,10)
- (6,14)
- (30,50)
- (40,60)
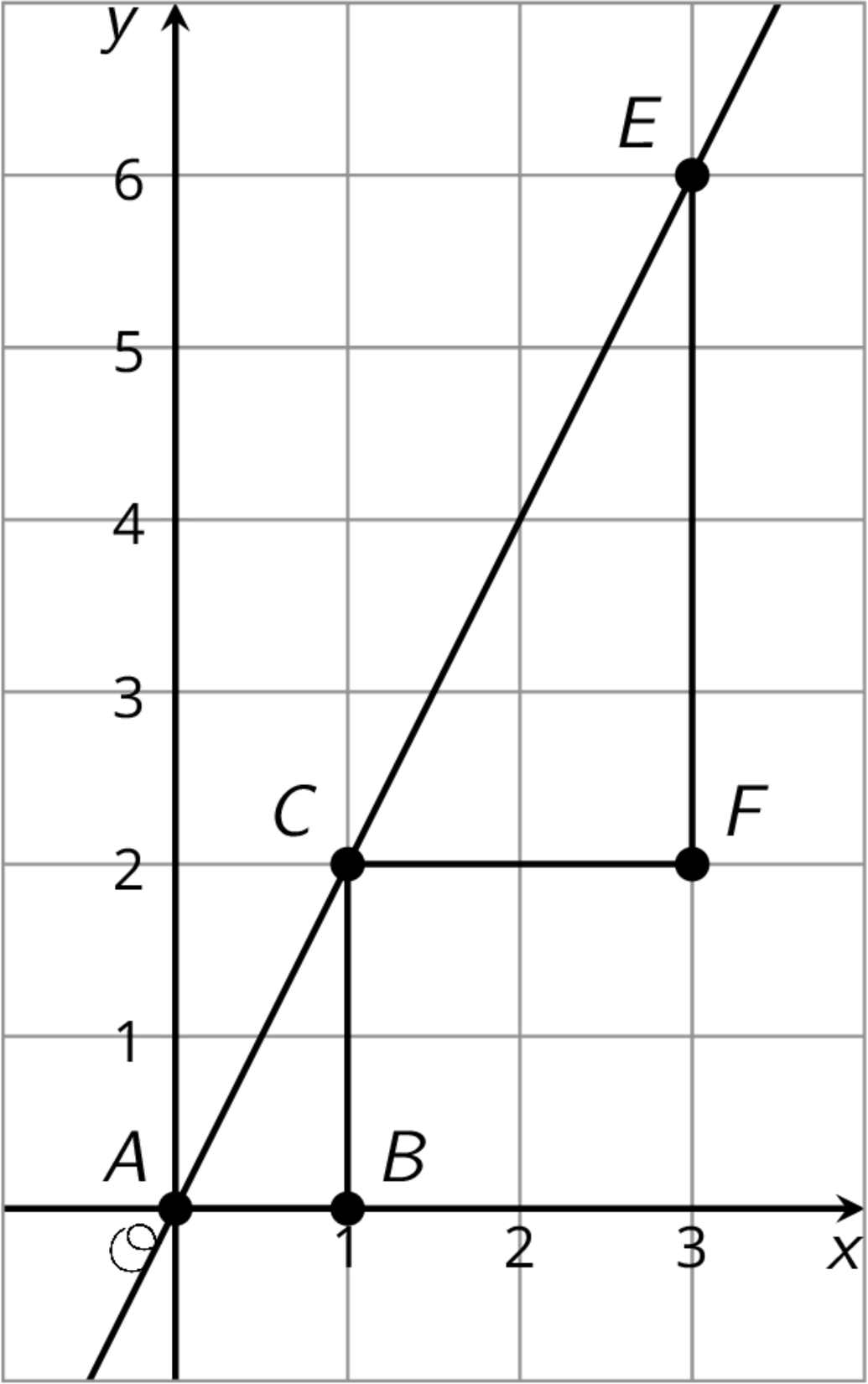
Problem 2
All three points displayed are on the line. Find an equation relating x and y.

Problem 3
Here is triangle ABC.
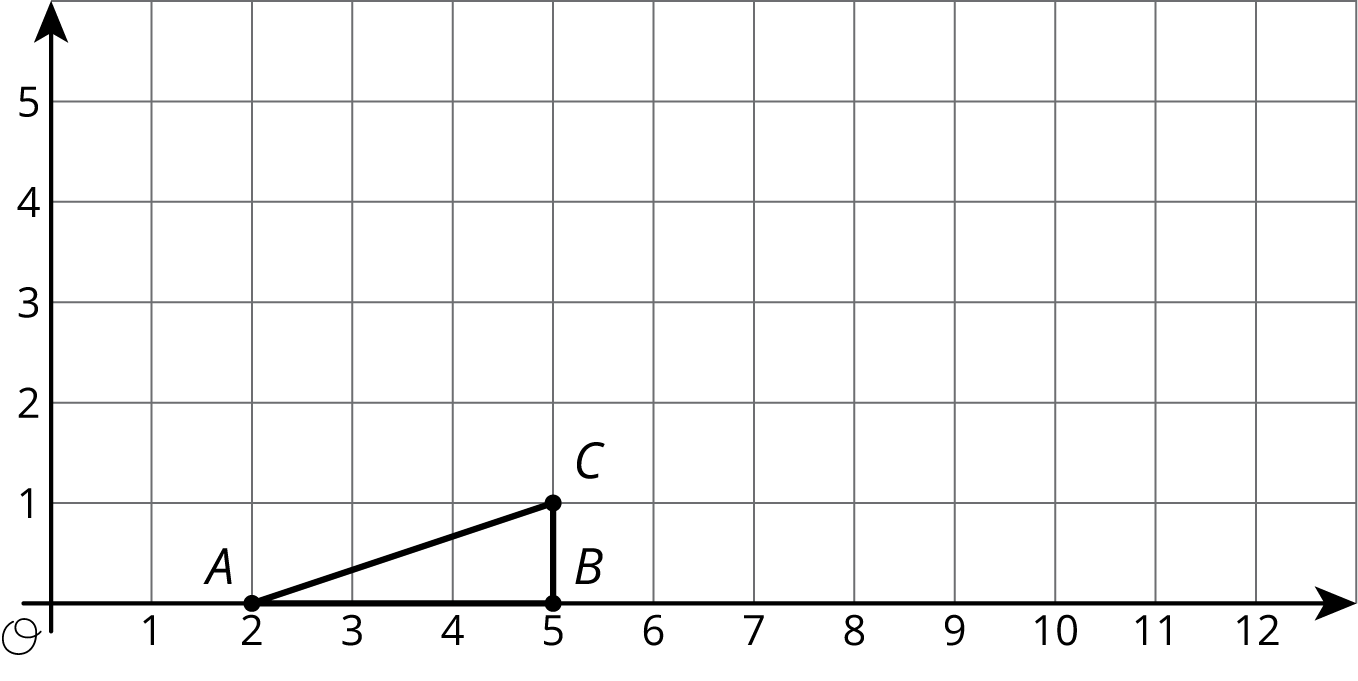
- Draw the dilation of triangle ABC with center (2,0) and scale factor 2.
- Draw the dilation of triangle ABC with center (2,0) and scale factor 3.
- Draw the dilation of triangle ABC with center (2,0) and scale factor \frac 1 2.
- What are the coordinates of the image of point C when triangle ABC is dilated with center (2,0) and scale factor s?
- Write an equation for the line containing all possible images of point C.
Problem 4 (from Unit 2, Lesson 4)
Here are some line segments.

- Which segment is a dilation of \overline{BC} using A as the center of dilation and a scale factor of \frac23?
- Which segment is a dilation of \overline{BC} using A as the center of dilation and a scale factor of \frac32?
- Which segment is not a dilation of \overline{BC}, and how do you know?
Lesson 13
No practice problems for this lesson.