16.1: True or False: Computational Relationships
Is each equation true or false?
62-28= 60-30
3\boldcdot \text{-}8= (2\boldcdot \text{-}8) - 8
Let’s see why the angles in a triangle add to 180 degrees.
Is each equation true or false?
62-28= 60-30
3\boldcdot \text{-}8= (2\boldcdot \text{-}8) - 8
Here is triangle ABC.
Select the Midpoint tool  and click on two points or a segment to find the midpoint.
and click on two points or a segment to find the midpoint.
Rotate triangle ABC 180^\circ around the midpoint of side AC. Right click on the point and select Rename to label the new vertex D.
Rotate triangle ABC 180^\circ around the midpoint of side AB. Right click on the point and select Rename to label the new vertex E.
Look at angles EAB, BAC, and CAD. Without measuring, write what you think is the sum of the measures of these angles. Explain or show your reasoning.
Is the measure of angle EAB equal to the measure of any angle in triangle ABC? If so, which one? If not, how do you know?
Is the measure of angle CAD equal to the measure of any angle in triangle ABC? If so, which one? If not, how do you know?
What is the sum of the measures of angles ABC, BAC, and ACB?
Here is \triangle ABC. Line DE is parallel to line AC.
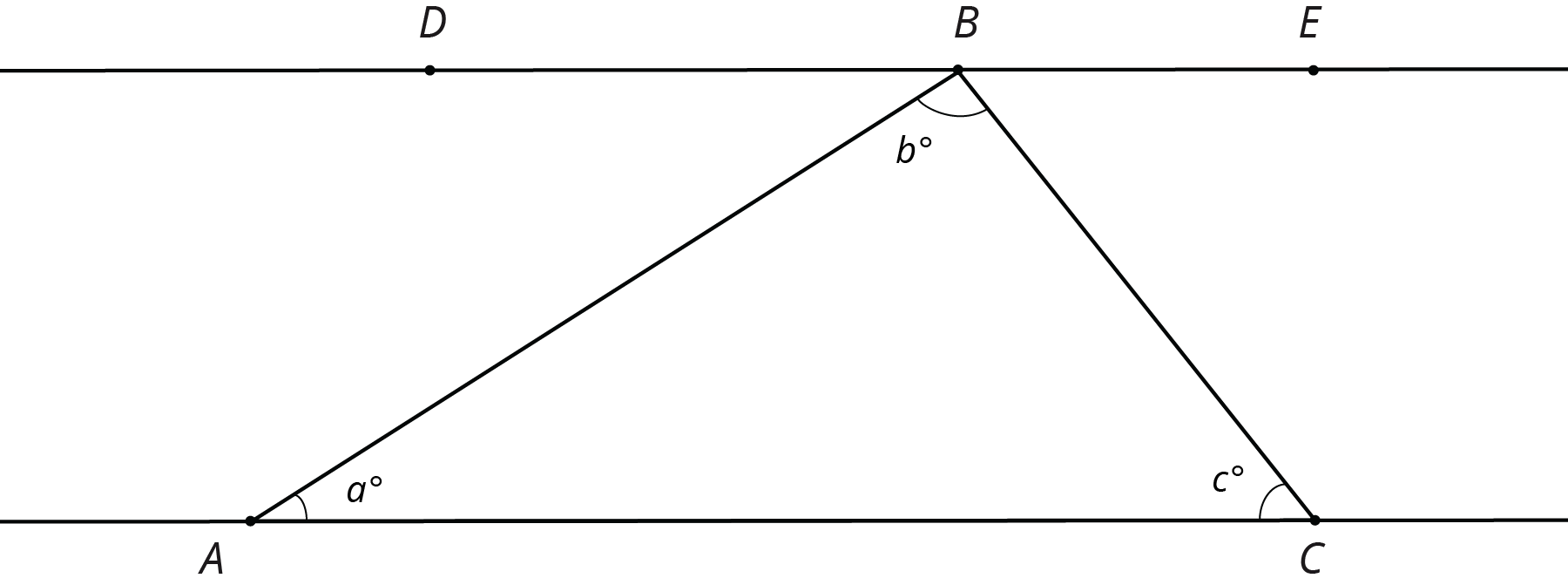
What is m{\angle DBA} + b + m{\angle CBE}? Explain how you know.
Explain why your argument will work for any triangle: that is, explain why the sum of the angle measures in any triangle is 180^\circ.
Using a ruler, create a few quadrilaterals. Use a protractor to measure the four angles inside the quadrilateral. What is the sum of these four angle measures?
This diagram shows a square BDFH that has been made by images of triangle ABC under rigid transformations.

Using parallel lines and rotations, we can understand why the angles in a triangle always add to 180^\circ. Here is triangle ABC. Line DE is parallel to AC and contains B.
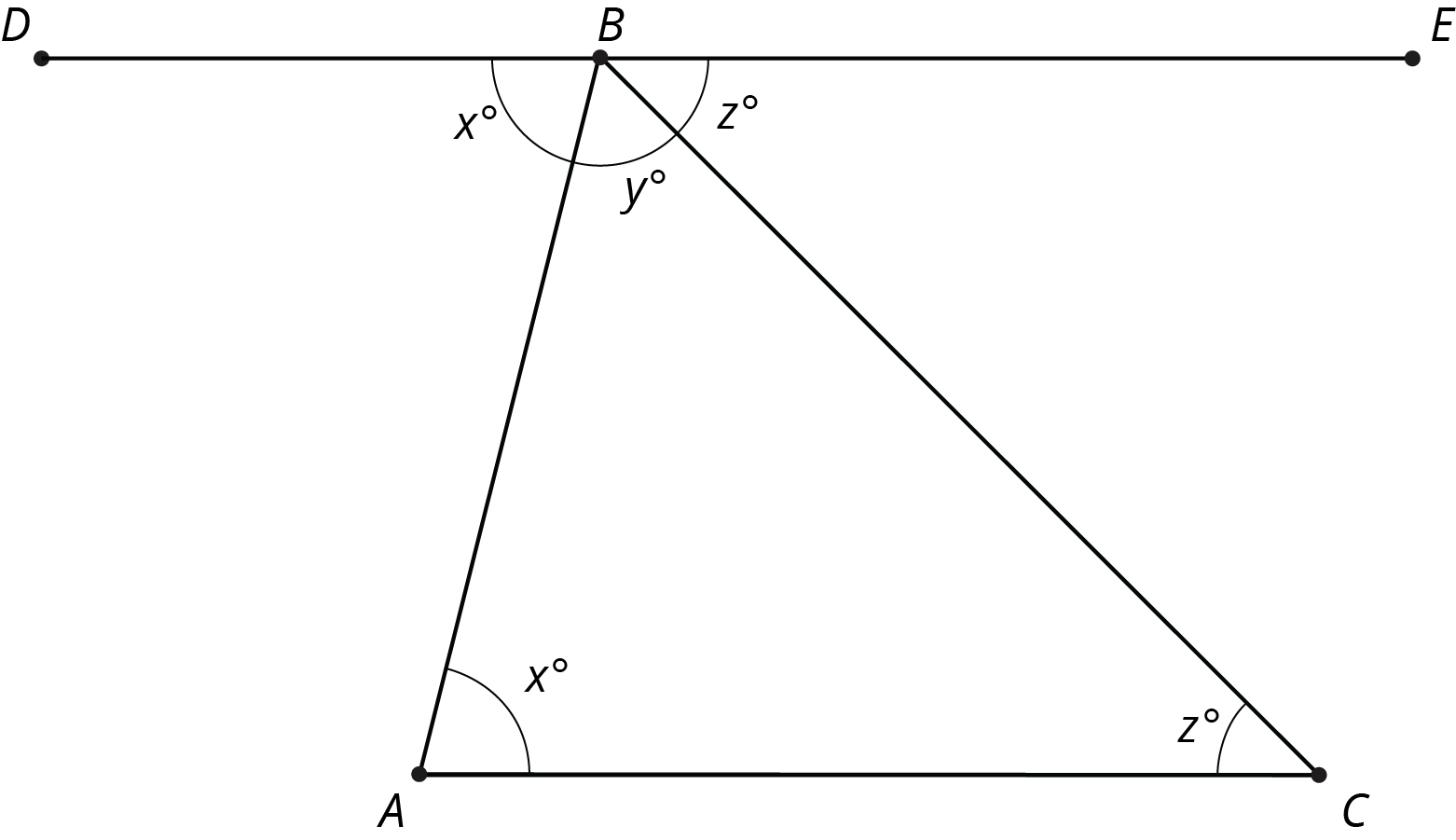
A 180 degree rotation of triangle ABC around the midpoint of AB interchanges angles A and DBA so they have the same measure: in the picture these angles are marked as x^\circ. A 180 degree rotation of triangle ABC around the midpoint of BC interchanges angles C and CBE so they have the same measure: in the picture, these angles are marked as z^\circ. Also, DBE is a straight line because 180 degree rotations take lines to parallel lines. So the three angles with vertex B make a line and they add up to 180^\circ (x + y + z = 180). But x, y, z are the measures of the three angles in \triangle ABC so the sum of the angles in a triangle is always 180^\circ!