Lesson 5: Negative Exponents with Powers of 10

Let’s see what happens when exponents are negative.

Solve each equation mentally.

$\frac{100}{1} = 10^x$

$\frac{100}{x} = 10^1$

$\frac{x}{100} = 10^0$

$\frac{100}{1,\!000} = 10^{x}$

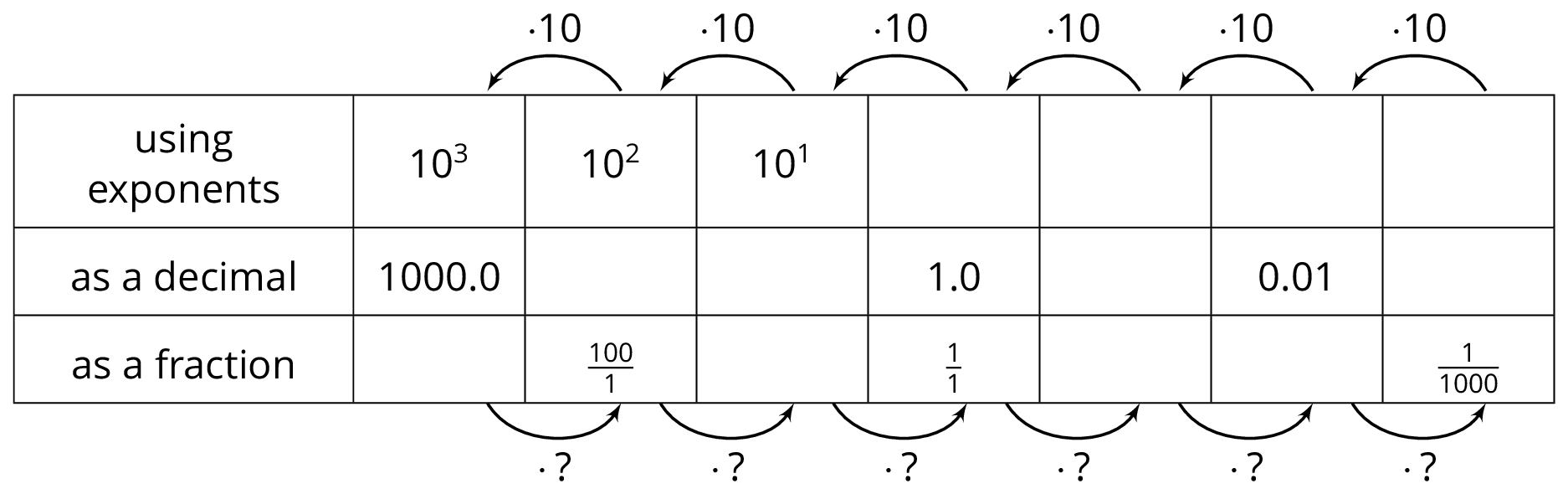
Complete the table to explore what negative exponents mean.

$An 8 column table with 3 rows of data. The first column contains a row header for each row. The data are as follows. Row 1: using exponents, 10 cubed; 10 squared; 10 to the first power; blank; blank; blank; blank. Row 2: as a decimal, 1000 point 0; blank; blank; 1 point 0; blank, 0 point 0 1; blank. Row 3: as a fraction, blank, the fraction 100 over 1; blank; the fraction 1 over 1; blank; blank; the fraction 1 over 1000. Above the table are arrows pointing from the 8th column to the 7th, the 7th column to the 6th, and so on. These arrows are labeled "mulitply by 10". Below the table are arrows pointing from the 2nd column to the 3rd, the 3rd column to the 4th, and so on. These arrows are labeled "mulitply by question mark".$

As you move toward the left, each number is being multiplied by 10. What is the multiplier as you move right?
How does each of these multipliers affect the placement of the decimal?
Use the patterns you found in the table to write $10^{\text -7}$ as a fraction.
Use the patterns you found in the table to write $10^{\text -5}$ as a decimal.
Write $\frac{1}{100,000,000}$ using a single exponent.
Use the patterns in the table to write $10^{\text -n}$ as a fraction.

Match the expressions that describe repeated multiplication in the same way:

Row 1	$\left(10^2\right)^3$	$\frac{1}{(10 \boldcdot 10)} \boldcdot \frac{1}{(10 \boldcdot 10)} \boldcdot \frac{1}{(10 \boldcdot 10)}$
Row 2	$\left(10^2\right)^{\text -3}$	$\left(\frac{1}{10} \boldcdot \frac{1}{10}\right)\left(\frac{1}{10} \boldcdot \frac{1}{10}\right)\left(\frac{1}{10} \boldcdot \frac{1}{10}\right)$
Row 3	$\left(10^{\text -2}\right)^3$	$\frac{1}{ \frac{1}{10} \boldcdot \frac{1}{10} }\boldcdot \frac{1}{ \frac{1}{10} \boldcdot \frac{1}{10} } \boldcdot \frac{1}{ \frac{1}{10} \boldcdot \frac{1}{10} }$
Row 4	$\left(10^{\text -2}\right)^{\text-3}$	$(10 \boldcdot 10)(10 \boldcdot 10)(10 \boldcdot 10)$

Write $(10^2)^{\text-3}$ as a power of 10 with a single exponent. Be prepared to explain your reasoning.

Match the expressions that describe repeated multiplication in the same way:

Row 1	$\frac{10^2}{10^5}$	$\frac{ \frac{1}{10} \boldcdot \frac{1}{10} }{ \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\boldcdot \frac{1}{10}\boldcdot \frac{1}{10} }$
Row 2	$\frac{10^2}{10^{\text -5}}$	$\frac{10 \boldcdot 10}{10 \boldcdot 10 \boldcdot 10 \boldcdot 10 \boldcdot 10}$
Row 3	$\frac{10^{\text -2}}{10^5}$	$\frac{ \frac{1}{10} \boldcdot \frac{1}{10} }{ 10 \boldcdot 10\boldcdot 10\boldcdot 10\boldcdot 10 }$
Row 4	$\frac{10^{\text -2}}{10^{\text -5}}$	$\frac{ 10 \boldcdot 10 }{ \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\boldcdot \frac{1}{10}\boldcdot \frac{1}{10}}$

Write $\frac{10^{\text -2}}{10^{\text -5}}$ as a power of 10 with a single exponent. Be prepared to explain your reasoning.

Match the expressions that describe repeated multiplication in the same way:

Row 1	$10^4 \boldcdot 10^3$	$(10 \boldcdot 10 \boldcdot 10 \boldcdot 10) \boldcdot ( \frac{1}{10} \boldcdot \frac{1}{10}\boldcdot \frac{1}{10})$
Row 2	$10^4 \boldcdot 10^{\text -3}$	$\left(\frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\right) \boldcdot \left( \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\right)$
Row 3	$10^{\text -4} \boldcdot 10^3$	$\left(\frac{1}{10}\boldcdot \frac{1}{10} \boldcdot \frac{1}{10} \boldcdot \frac{1}{10}\right) \boldcdot \left(10 \boldcdot 10 \boldcdot 10\right)$
Row 4	$10^{\text -4} \boldcdot 10^{\text -3}$	$(10 \boldcdot 10 \boldcdot 10 \boldcdot 10) \boldcdot (10 \boldcdot 10 \boldcdot 10)$

Write $10^{\text -4} \boldcdot 10^3$ as a power of 10 with a single exponent. Be prepared to explain your reasoning.

Are You Ready For More?

Priya, Jada, Han, and Diego are playing a game. They stand in a circle in this order and take turns playing a game.

Priya says, SAFE. Jada, standing to Priya's left, says, OUT and leaves the circle. Han is next: he says, SAFE. Then Diego says, OUT and leaves the circle. At this point, only Priya and Han are left. They continue to alternate. Priya says, SAFE. Han says, OUT and leaves the circle. Priya is the only person left, so she is the winner.

Priya says, “I knew I’d be the only one left, since I went first.”

Record this game on paper a few times with different numbers of players. Does the person who starts always win?
Try to find as many numbers as you can where the person who starts always wins. What patterns do you notice?

Summary

When we multiply a positive power of 10 by $\frac{1}{10}$ , the exponent decreases by 1: $10^8 \boldcdot \frac{1}{10} = 10^7$ This is true for any positive power of 10. We can reason in a similar way that multiplying by 2 factors that are $\frac{1}{10}$ decreases the exponent by 2: $\left(\frac{1}{10}\right)^2 \boldcdot 10^8 = 10^6$

That means we can extend the rules to use negative exponents if we make $10^{\text-2} = \left(\frac{1}{10}\right)^2$ . Just as $10^2$ is two factors that are 10, we have that $10^{\text-2}$ is two factors that are $\frac{1}{10}$ . More generally, the exponent rules we have developed are true for any integers $n$ and $m$ if we make $10^{\text-n} = \left(\frac{1}{10}\right)^n = \frac{1}{10^n}$

Here is an example of extending the rule $\frac{10^n}{10^m} = 10^{n-m}$ to use negative exponents: $\frac{10^3}{10^5} = 10^{3-5} = 10^{\text-2}$ To see why, notice that $\frac{10^3}{10^5} = \frac{10^3}{10^3 \boldcdot 10^2} = \frac{10^3}{10^3} \boldcdot \frac{1}{10^2} = \frac{1}{10^2}$ which is equal to $10^{\text-2}$ .

Here is an example of extending the rule $\left(10^m\right)^n = 10^{m \boldcdot n}$ to use negative exponents: $\left(10^{\text-2}\right)^{3} = 10^{(\text-2)(3)}=10^{\text-6}$ To see why, notice that $10^{\text-2} = \frac{1}{10} \boldcdot \frac{1}{10}$ . This means that $\left(10^{\text-2}\right)^{3} =\left( \frac{1}{10} \boldcdot \frac{1}{10}\right)^3 = \left(\frac{1}{10} \boldcdot \frac{1}{10}\right) \boldcdot \left( \frac{1}{10} \boldcdot \frac{1}{10}\right)\boldcdot \left(\frac{1}{10}\boldcdot \frac{1}{10}\right) = \frac{1}{10^6} = 10^{\text-6}$

Lesson 5: Negative Exponents with Powers of 10

5.1: Number Talk: What's That Exponent?

5.2: Negative Exponent Table

5.3: Follow the Exponent Rules

Are You Ready For More?

Summary

Practice Problems ▶