Lesson 3: Equations for Functions

Let’s find outputs from equations.

3.1: A Square’s Area

Fill in the table of input-output pairs for the given rule. Write an algebraic expression for the rule in the box in the diagram.

  input output
row 1 8  
row 2 2.2  
row 3 12\frac14  
row 4 s  

3.2: Diagrams, Equations, and Descriptions

Record your answers to these questions in the table provided:

  1. Match each of these descriptions with a diagram:
    1. the circumference, C, of a circle with radius, r
    2. the distance in miles, d, that you would travel in t hours if you drive at 60 miles per hour
    3. the output when you triple the input and subtract 4
    4. the volume of a cube, v given its edge length, s
  2. Write an equation for each description that expresses the output as a function of the input.
  3. Find the output when the input is 5 for each equation.
  4. Name the independent and dependent variables of each equation.
description a b c d
diagram                    
 		                                                                  
equation  
 		      
input = 5
output = ?		        
independent
variable		        
dependent
variable		        

3.3: Dimes and Quarters

Jada had some dimes and quarters that had a total value of $12.50. The relationship between the number of dimes, d, and the number of quarters, q, can be expressed by the equation 0.1d + 0.25q = 12.5.

  1. If Jada has 4 quarters, how many dimes does she have?
  2. If Jada has 10 quarters, how many dimes does she have?
  3. Is the number of dimes a function of the number of quarters? If yes, write a rule (that starts with d = ...) that you can use to determine the output, d, from a given input, q. If no, explain why not.
  4. If Jada has 25 dimes, how many quarters does she have?
  5. If Jada has 30 dimes, how many quarters does she have?
  6. Is the number of quarters a function of the number of dimes? If yes, write a rule (that starts with q=...) that you can use to determine the output, q, from a given input, d. If no, explain why not.

Summary

We can sometimes represent functions with equations. For example, the area, A, of a circle is a function of the radius, r, and we can express this with an equation: A=\pi r^2

We can also draw a diagram to represent this function:

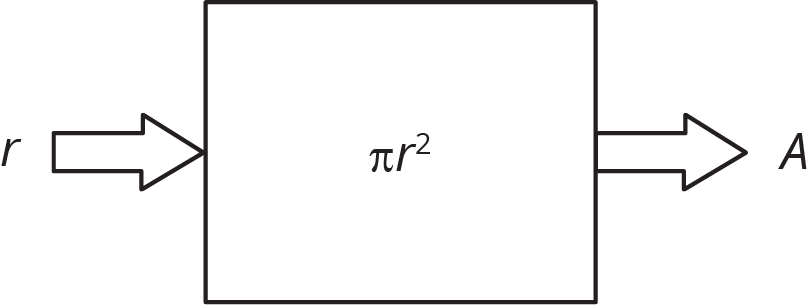
In this case, we think of the radius, r, as the input, and the area of the circle, A, as the output. For example, if the input is a radius of 10 cm, then the output is an area of 100\pi cm2, or about 314 square cm. Because this is a function, we can find the area, A, for any given radius, r.

Since it is the input, we say that r is the independent variable and, as the output, A is the dependent variable.

Sometimes when we have an equation we get to choose which variable is the independent variable. For example, if we know that

10A-4B=120

then we can think of A as a function of B and write

A=0.4B+12

or we can think of B as a function of A and write

B=2.5A-30

Practice Problems ▶

Glossary

independent variable

independent variable

A variable representing the input of a function.

dependent variable

dependent variable

A variable representing the output of a function.