3.1: Algebra Talk: Positive Solutions
Find a positive solution to each equation:
- $x^2=36$
- $x^2=\frac94$
- $x^2=\frac14$
- $x^2=\frac{49}{25}$
Let’s learn about irrational numbers.
Find a positive solution to each equation:

For each square:
Label the area.
Label the side length.
Write an equation that shows the relationship between the side length and the area.
Are any of these numbers a solution to the equation $x^2=2$? Explain your reasoning.
1
$\frac12$
$\frac32$
A rational number is a fraction or its opposite (or any number equivalent to a fraction or its opposite).
If you have an older calculator evaluate the expression$$\left(\frac{577}{408}\right)^2$$and it will tell you that the answer is 2, which might lead you to think that $\sqrt{2}=\frac{577}{408}$.
In an earlier activity, we learned that square root notation is used to write the length of a side of a square given its area. For example, a square whose area is 2 square units has a side length of $\sqrt{2}$ units, which means that$$\sqrt{2} \boldcdot \sqrt{2} = 2.$$
A square whose area is 25 square units has a side length of $\sqrt{25}$ units, which means that $$\sqrt{25} \boldcdot \sqrt{25} = 25.$$Since $5 \boldcdot 5 = 25$, we know that $$\sqrt{25}=5.$$
$\sqrt{25}$ is an example of a rational number. A rational number is a fraction or its opposite. Remember that a fraction $\frac{a}{b}$ is a point on the number line found by dividing the segment from 0 to 1 into $b$ equal intervals and going $a$ of those intervals to the right of 0. We can always write a fraction in the form $\frac{a}{b}$ where $a$ and $b$ are whole numbers (and $b$ is not 0), but there are other ways to write them. For example, we can write $\sqrt{25} = \frac{5}{1}$. You first learned about fractions in earlier grades, and at that time, you probably didn't know about negative numbers. Rational numbers are fractions, but they can be positive or negative. So, -5 is also a rational number. Because fractions and ratios are closely related ideas, fractions and their opposites are called RATIOnal numbers.
An irrational number is a number that is not rational. That is, it is a number that is not a fraction or its opposite. $\sqrt{2}$ is an example of an irrational number. It has a location on the number line, and its location can be approximated by rational numbers (it's a tiny bit to the right of $\frac75$), but $\sqrt{2}$ can not be found on a number line by dividing the segment from 0 to 1 into $b$ equal parts and going $a$ of those parts away from 0 (if $a$ and $b$ are whole numbers).
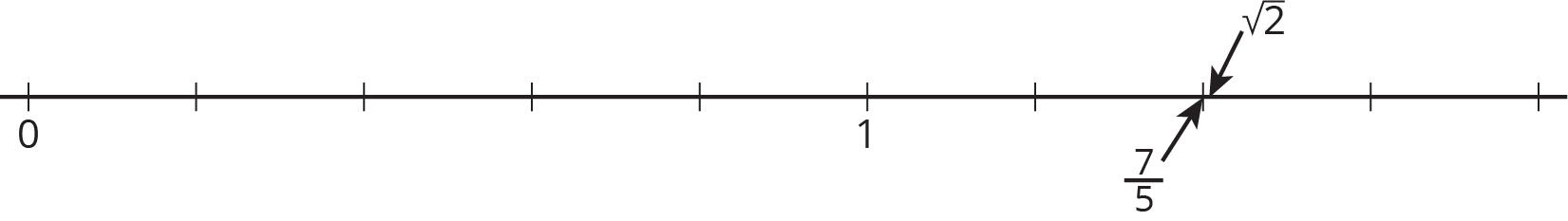
$\frac{17}{12}$ is also close to $\sqrt{2}$, because $\left( \frac{17}{12} \right)^2=\frac{289}{144}$. $\frac{289}{144}$ is very close to 2, since $\frac{288}{144}=2$. But we could keep looking forever for solutions to $x^2=2$ that are rational numbers, and we would not find any. $\sqrt2$ is not a rational number! It is irrational.
In your future studies, you may have opportunities to understand or write a proof that $\sqrt2$ is irrational, but for now, we just take it as a fact that $\sqrt2$ is irrational. Similarly, the square root of any whole number is either a whole number ($\sqrt{36}=6$, $\sqrt{64}=8$, etc.) or irrational ($\sqrt{17}$, $\sqrt{65}$, etc.). Here are some other examples of irrational numbers:$$\sqrt{10}, \text{ -}\sqrt3, \text{ }\frac{\sqrt5}{2},\text{ } \pi$$
An irrational number is a number that is not rational. That is, it cannot be expressed as a positive or negative fraction, or zero.
A rational number is a fraction or the opposite of a fraction. Remember that a fraction is a point on the number line that you get by dividing the unit interval into $b$ equal parts and finding the point that is $a$ of them from 0. We can always write a fraction in the form $\frac{a}{b}$ where $a$ and $b$ are whole numbers, with $b$ not equal to 0, but there are other ways to write them. For example, 0.7 is a fraction because it is the point on the number line you get by dividing the unit interval into 10 equal parts and finding the point that is 7 of those parts away from 0. We can also write this number as $\frac{7}{10}$.