Lesson 5: More Dilations

Let’s look at dilations in the coordinate plane.

Explore the applet and observe the dilation of triangle $ABC$ . The dilation always uses center $P$ , but you can change the scale factor. What connections can you make between the scale factor and the dilated triangle?

GeoGebra Applet jjRtyeJX

Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

If your teacher gives you the problem card:

Silently read your card and think about what information you need to answer the question.
Ask your partner for the specific information that you need.
Explain to your partner how you are using the information to solve the problem.
Solve the problem and explain your reasoning to your partner.

If your teacher gives you the data card:

Silently read the information on your card.
Ask your partner “What specific information do you need?” and wait for your partner to ask for information. Only give information that is on your card. (Do not figure out anything for your partner!)
Before telling your partner the information, ask “Why do you need that information?”
After your partner solves the problem, ask them to explain their reasoning and listen to their explanation.

Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.

Are You Ready For More?

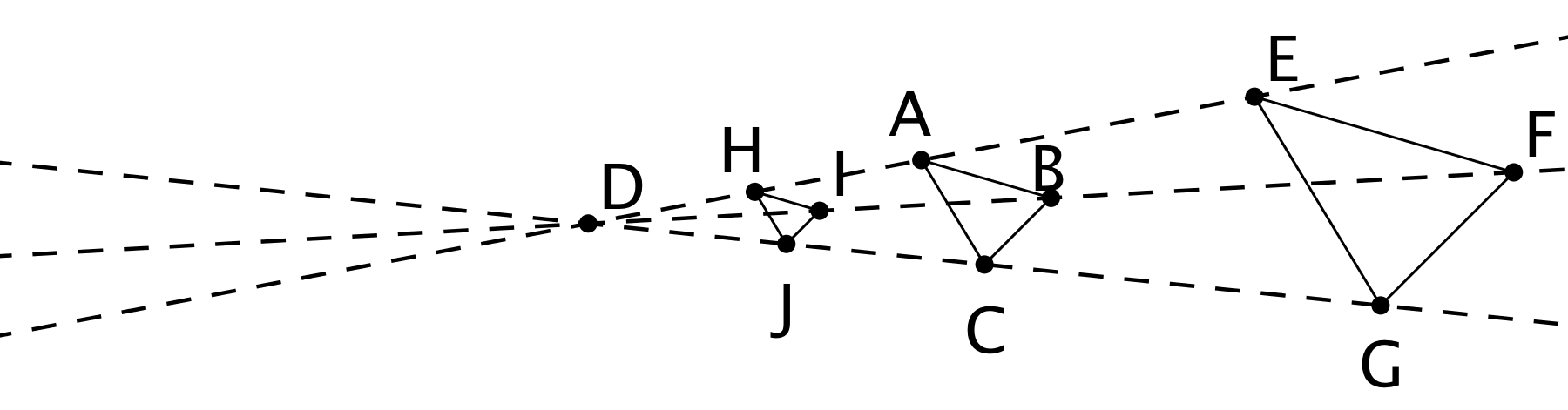
Triangle $EFG$ was created by dilating triangle $ABC$ using a scale factor of 2 and center $D$ . Triangle $HIJ$ was created by dilating triangle $ABC$ using a scale factor of $\frac12$ and center $D$ .

What would the image of triangle $ABC$ look like under a dilation with scale factor 0?
What would the image of the triangle look like under dilation with a scale factor of -1? If possible, draw it and label the vertices $A’$ , $B’$ , and $C’$ . If it’s not possible, explain why not.
If possible, describe what happens to a shape if it is dilated with a negative scale factor. If dilating with a negative scale factor is not possible, explain why not.

Summary

One important use of coordinates is to communicate geometric information precisely. Let’s consider a quadrilateral $ABCD$ in the coordinate plane. Performing a dilation of $ABCD$ requires three vital pieces of information:

The coordinates of $A$ , $B$ , $C$ , and $D$
The coordinates of the center of dilation, $P$
The scale factor of the dilation

With this information, we can dilate the vertices $A$ , $B$ , $C$ , and $D$ and then draw the corresponding segments to find the dilation of $ABCD$ . Without coordinates, describing the location of the new points would likely require sharing a picture of the polygon and the center of dilation.

Lesson 5: More Dilations

5.1: Many Dilations of a Triangle

5.2: Info Gap: Dilations

Are You Ready For More?

Summary

Practice Problems ▶