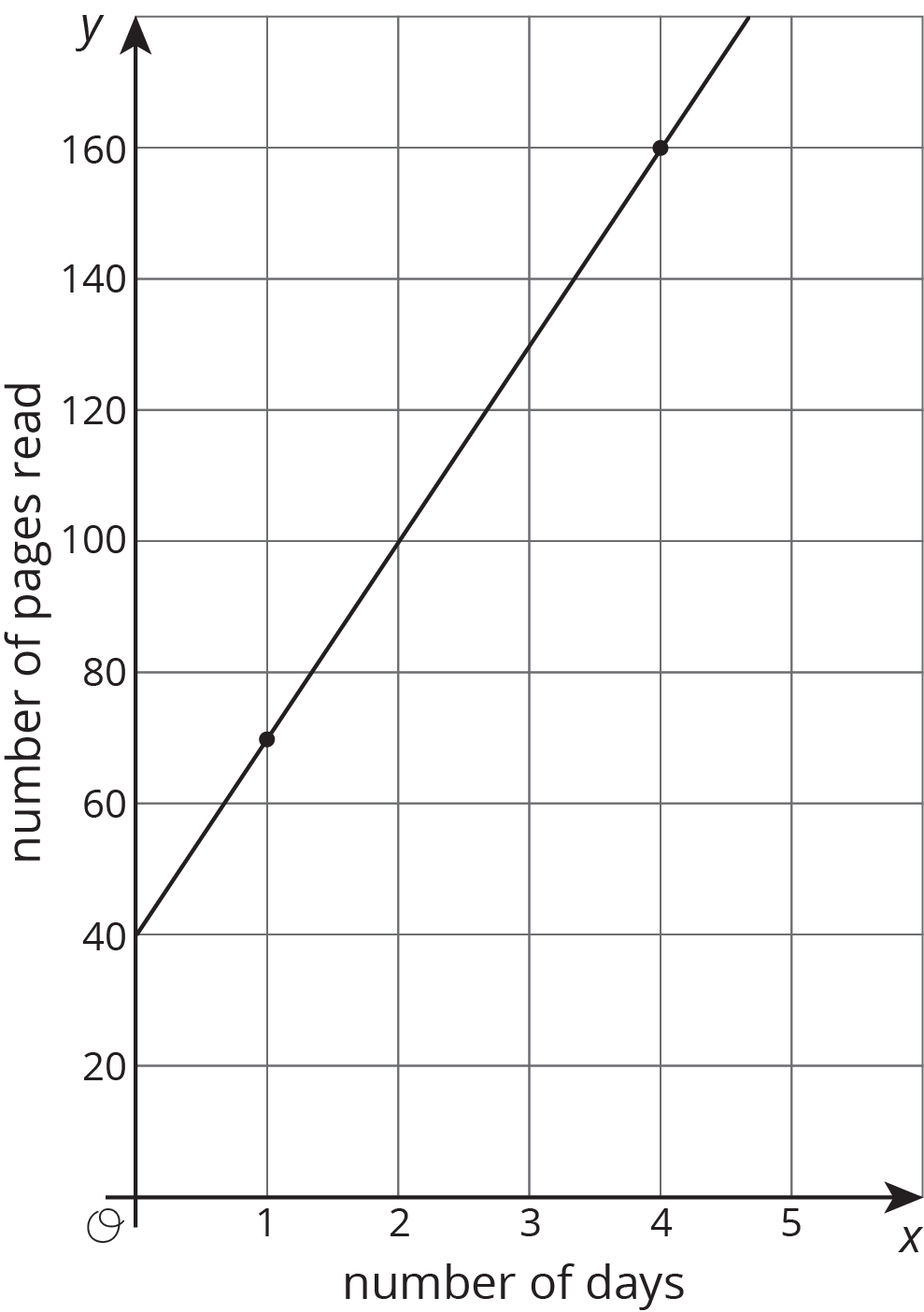
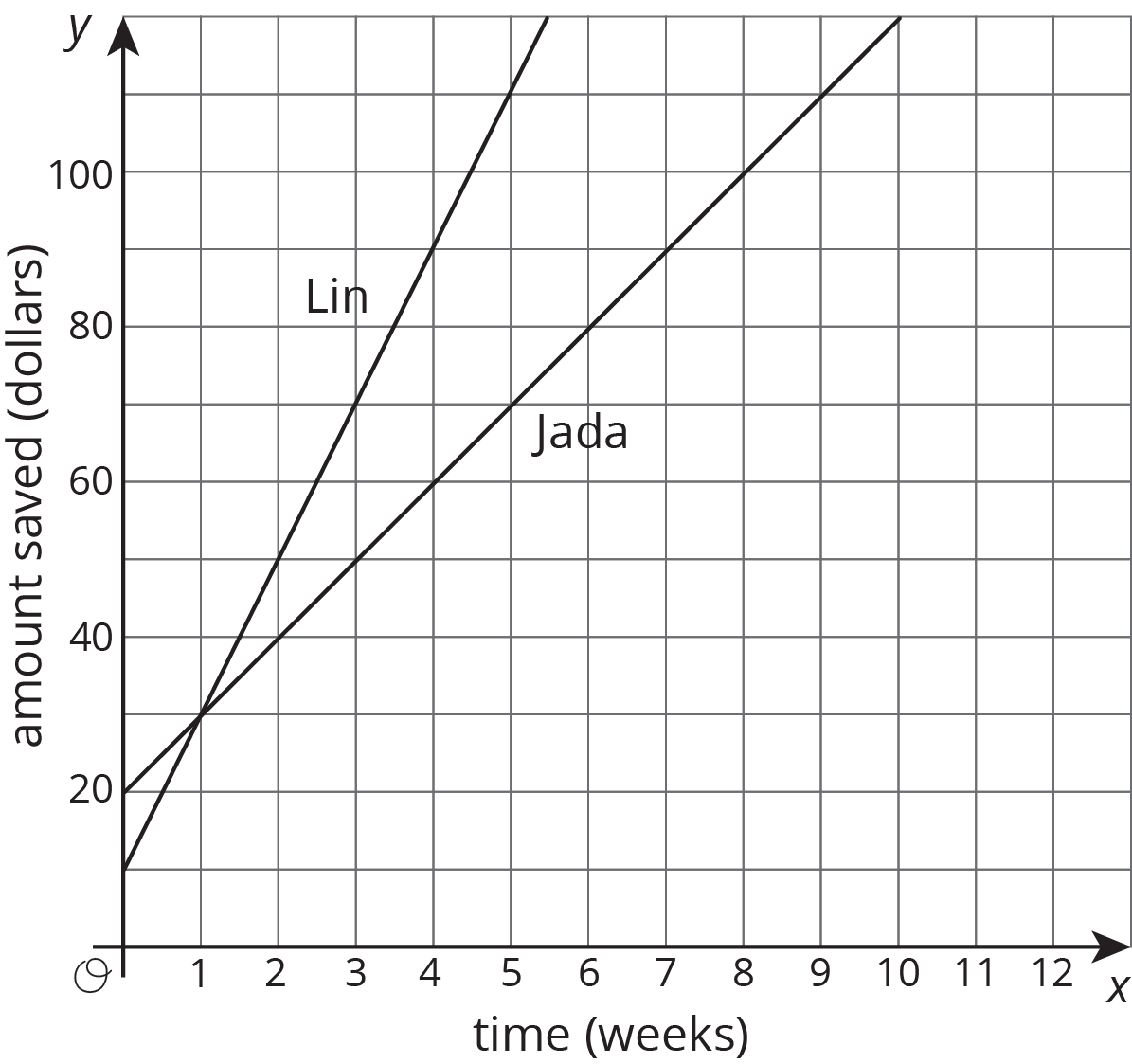
6.1: Growing
Look for a growing pattern. Describe the pattern you see.
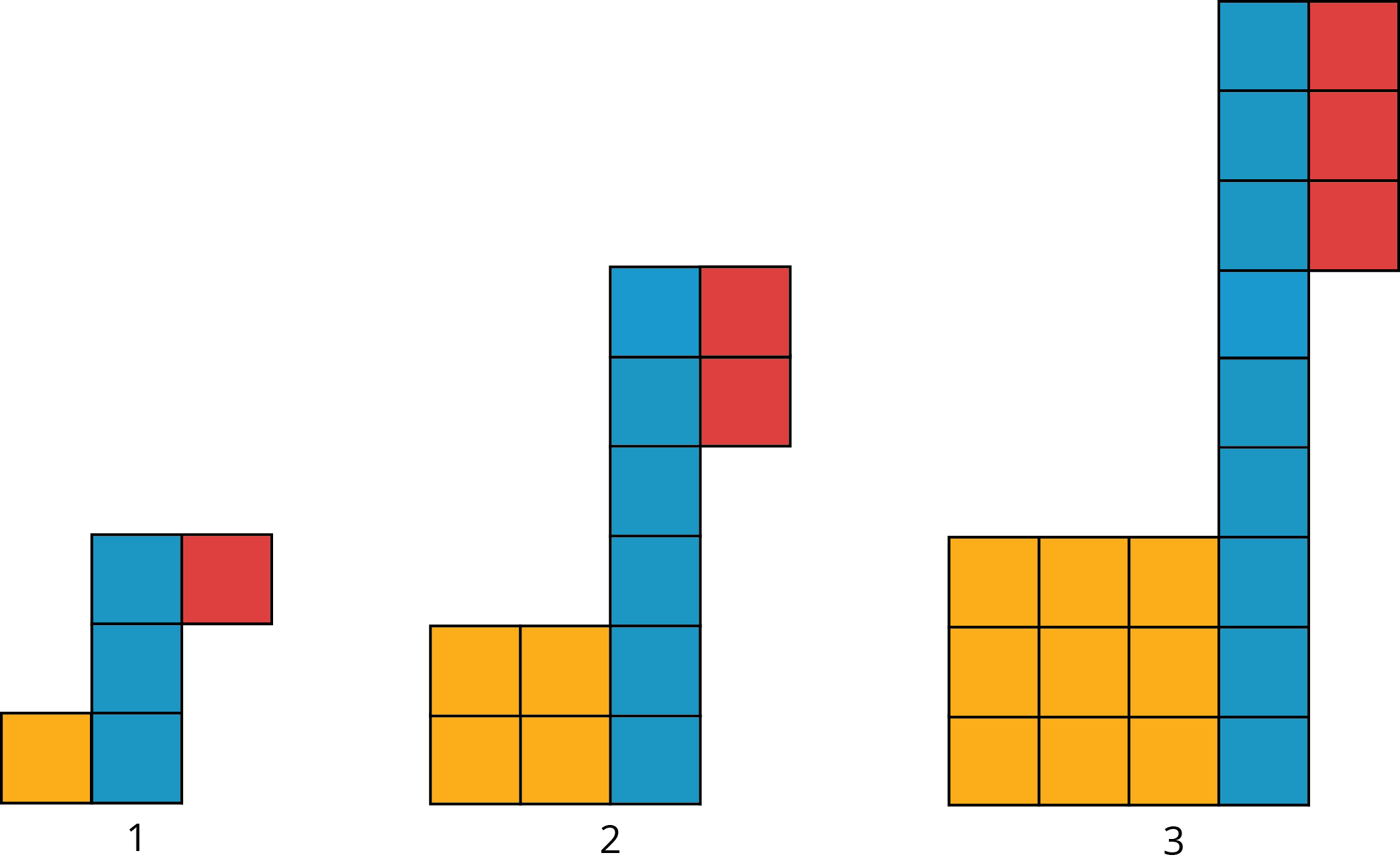
-
If your pattern continues growing in the same way, how many tiles of each color will be in the 4th and 5th diagram? The 10th diagram?
-
How many tiles of each color will be in the nth diagram? Be prepared to explain how your reasoning.