Lesson 11: Filling containers

Let’s fill containers with water.

11.1: Which One Doesn’t Belong: Solids

These are drawings of three-dimensional objects. Which one doesn’t belong? Explain your reasoning.

Four different, three-dimensional shapes labeled A, B, C, and D. Shape "A" is a cone; Shape "B" is a sphere; Shape "C" is a cylinder; Shape "D" is a rectangular prism.

11.2: Height and Volume

Use the applet to investigate the height of water in the cylinder as a function of the water volume.

  1. Before you get started, make a prediction about the shape of the graph.

  2. Check Reset and set the radius and height of the graduated cylinder to values you choose.

  3. Let the cylinder fill with different amounts of water and record the data in the table.

GeoGebra Applet M4668aNC

  1. Create a graph that shows the height of the water in the cylinder as a function of the water volume.
  2. Choose a point on the graph and explain its meaning in the context of the situation.
 
Drop Image Here
powered by

11.3: What Is the Shape?

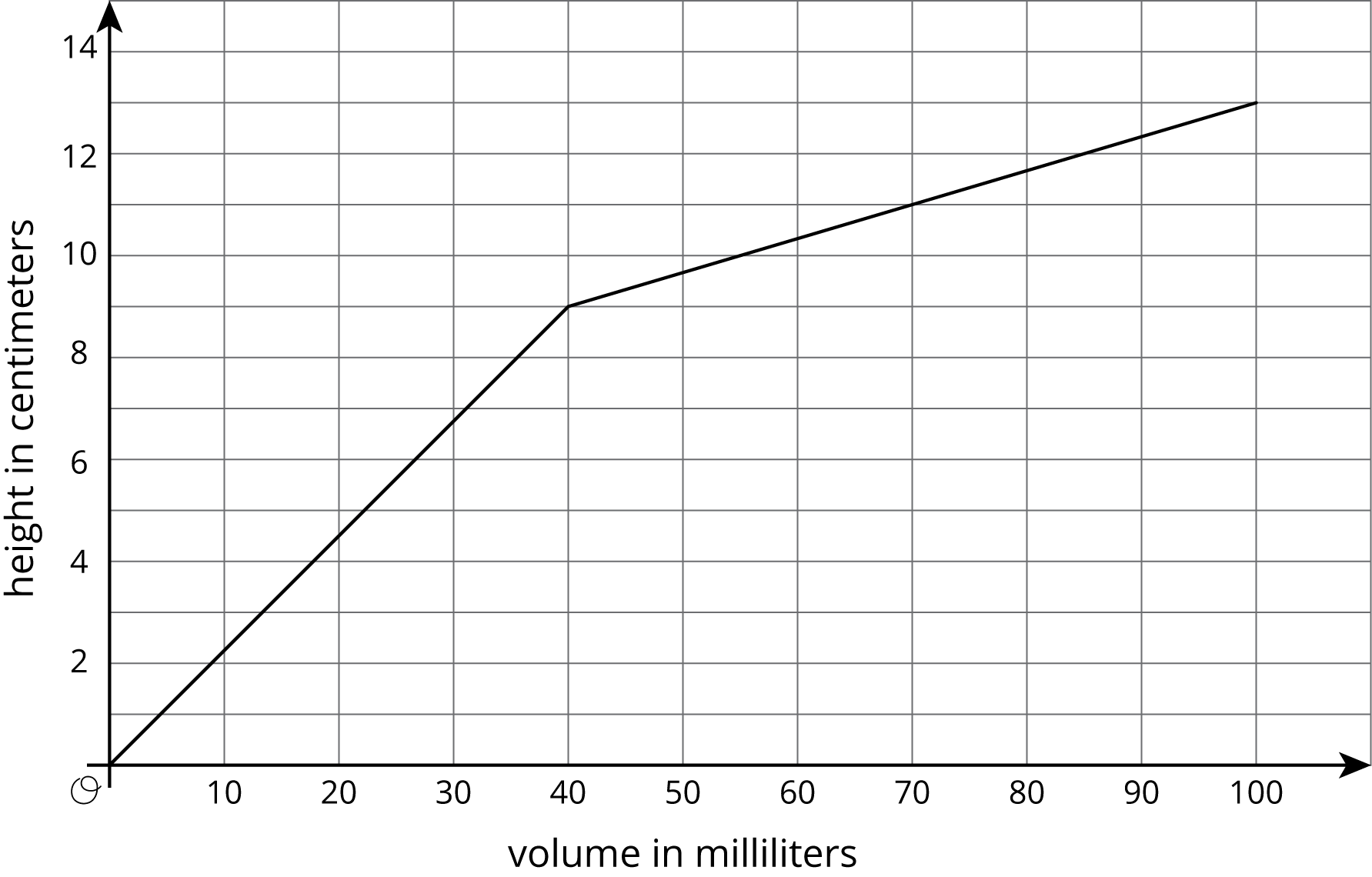
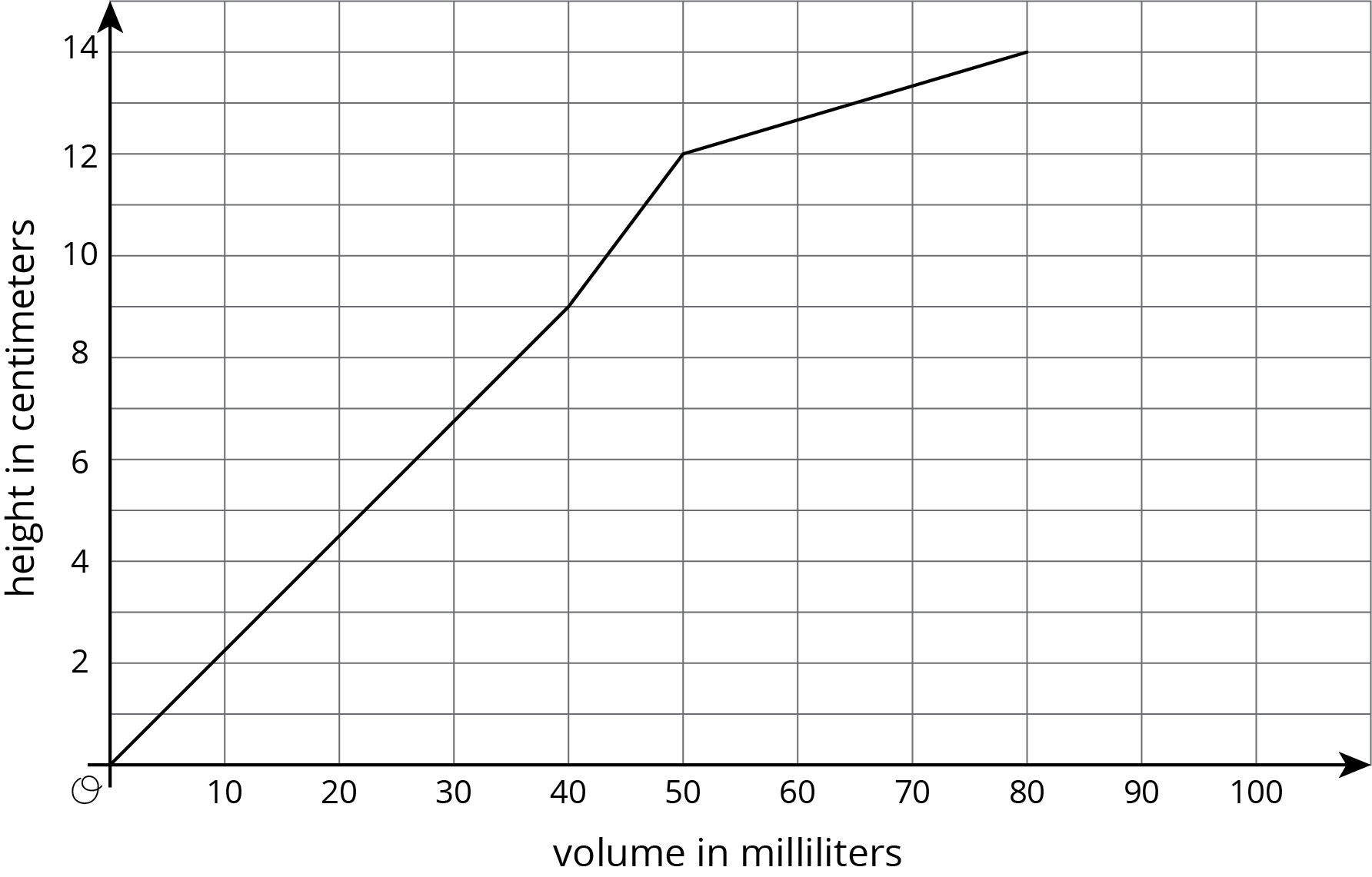
  1. The graph shows the height vs. volume function of an unknown container. What shape could this container have? Explain how you know and draw a possible container.
    The graph of two connected line segments on the coordinate plane with the origin labeled “O”. The horizontal axis is labeled “volume in millilters” and the numbers 0 through 100, in increments of 10, are indicated. The vertical axis is labeled “height in centimeters” and the numbers 0 through 14, in increments of 2, are indicated. The first line begins at the origin, moves steadily upward and to the right, ending at the point 40 comma 9. The second line segment begins where the first line segment ends, moves steadily upward and to the right passing through the point 70 comma 11 and ending at the point 100 comma 13.
  2. The graph shows the height vs. volume function of a different unknown container. What shape could this container have? Explain how you know and draw a possible container.
  3. How are the two containers similar? How are they different?

Summary

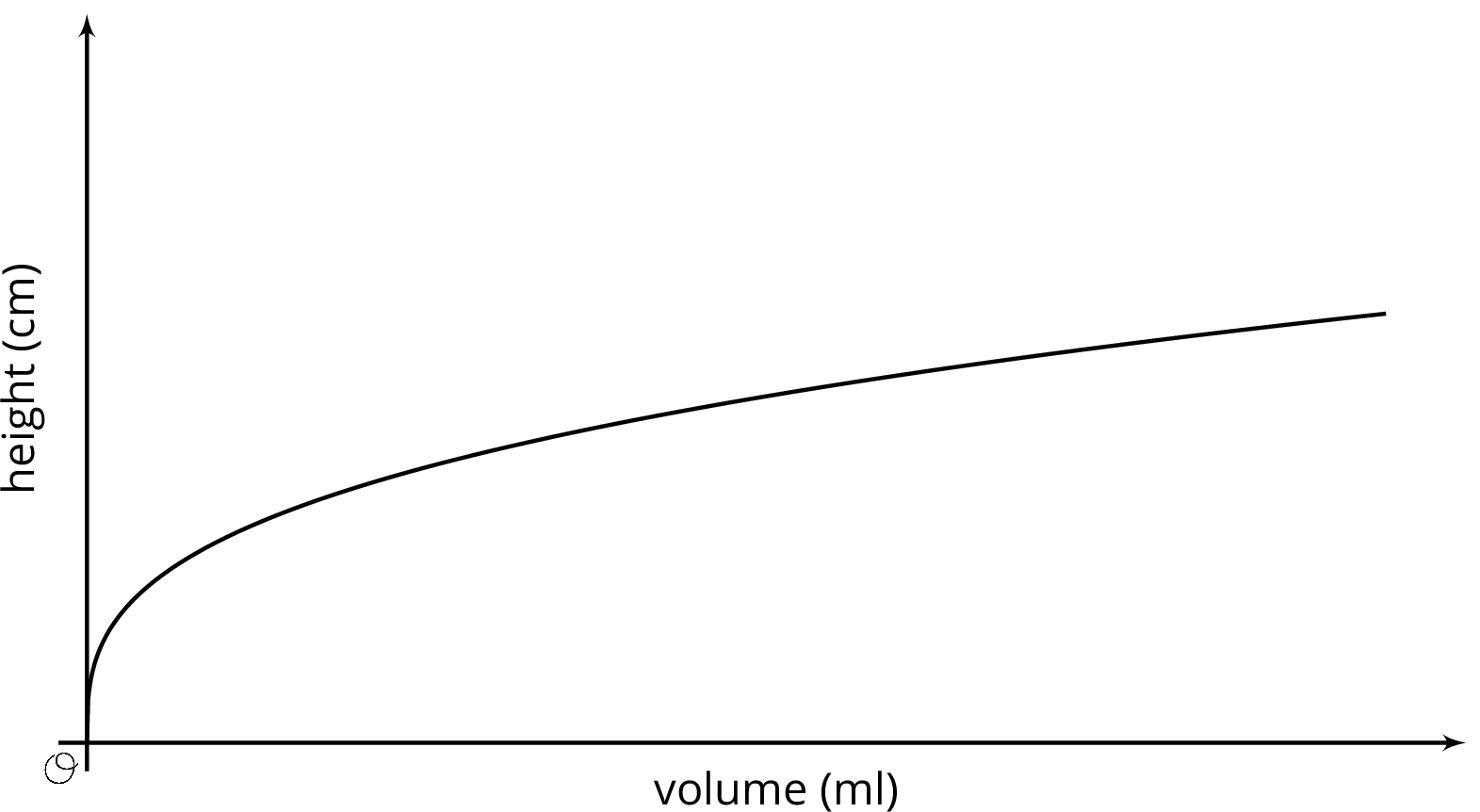
When filling a shape like a cylinder with water, we can see how the dimensions of the cylinder affect things like the changing height of the water. For example, let's say we have two cylinders, D and E, with the same height, but D has a radius of 3 cm and E has a radius of 6 cm.
 

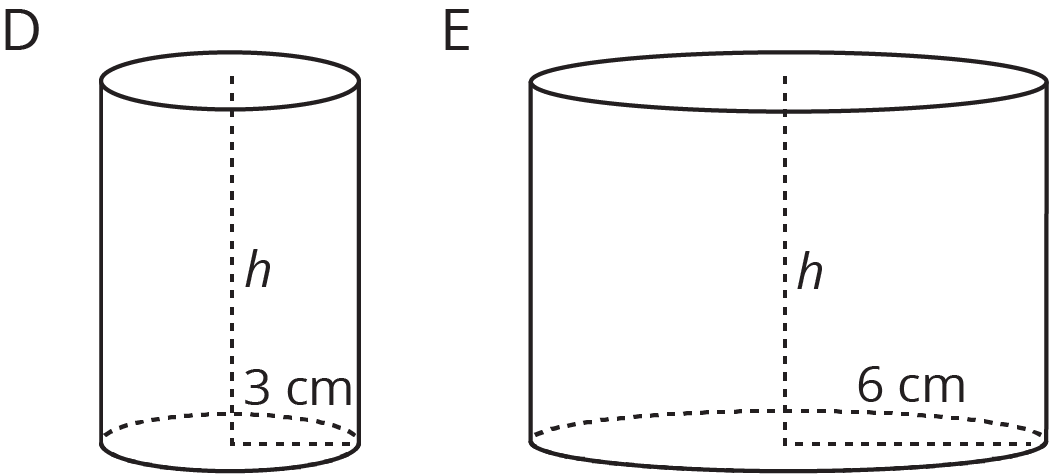
If we pour water into both cylinders at the same rate, the height of water in D will increase faster than the height of water in E due to its smaller radius. This means that if we made graphs of the height of water as a function of the volume of water for each cylinder, we would have two lines and the slope of the line for cylinder D would be greater than the slope of the line for cylinder E.

Practice Problems ▶