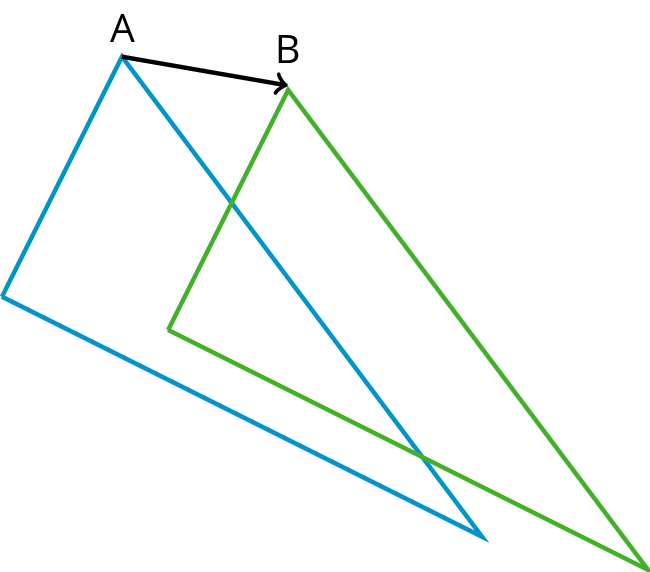
2.1: A Pair of Quadrilaterals
Quadrilateral A can be rotated into the position of Quadrilateral B.
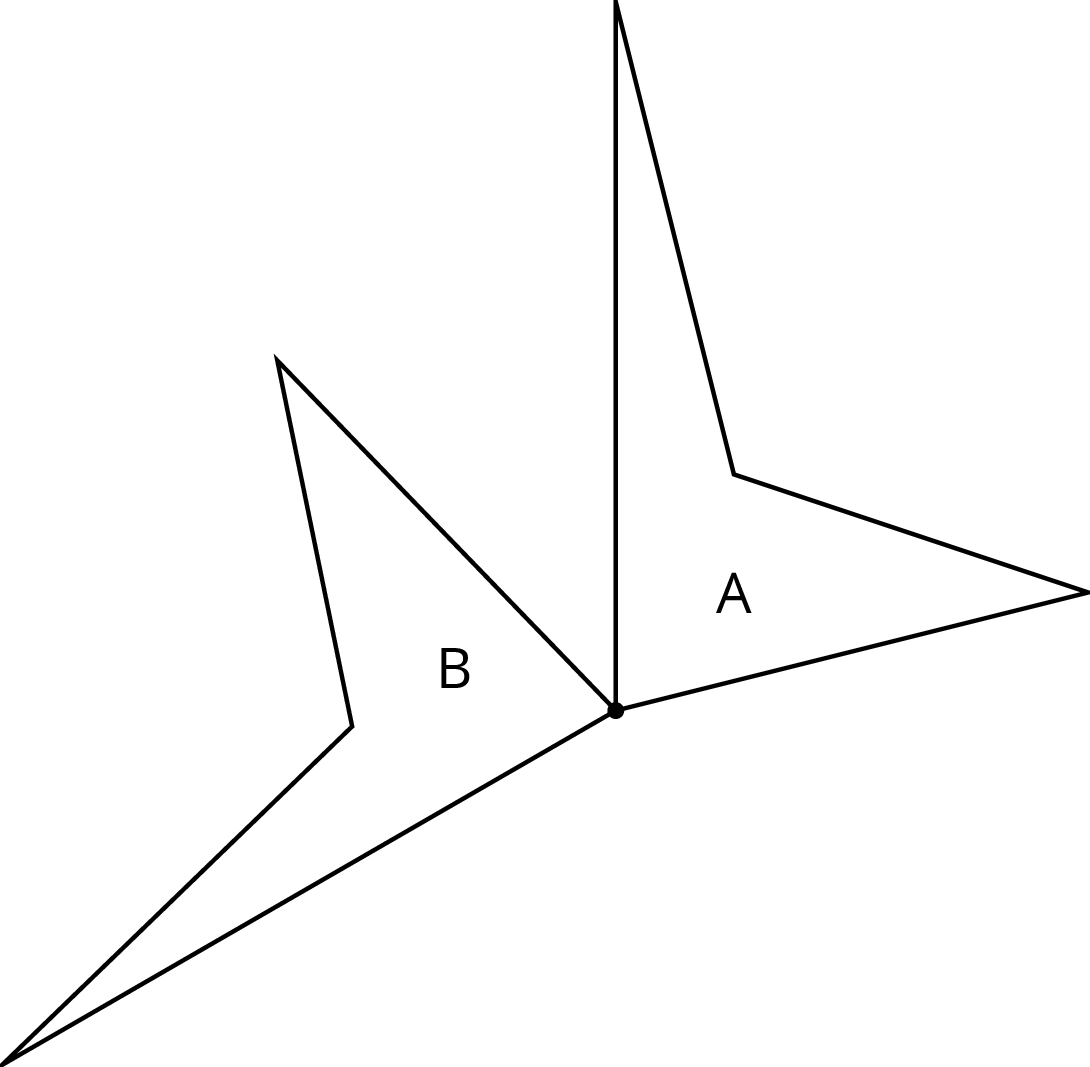
Let’s be more precise about describing moves of figures in the plane.
Quadrilateral A can be rotated into the position of Quadrilateral B.

Here is another set of dance moves.
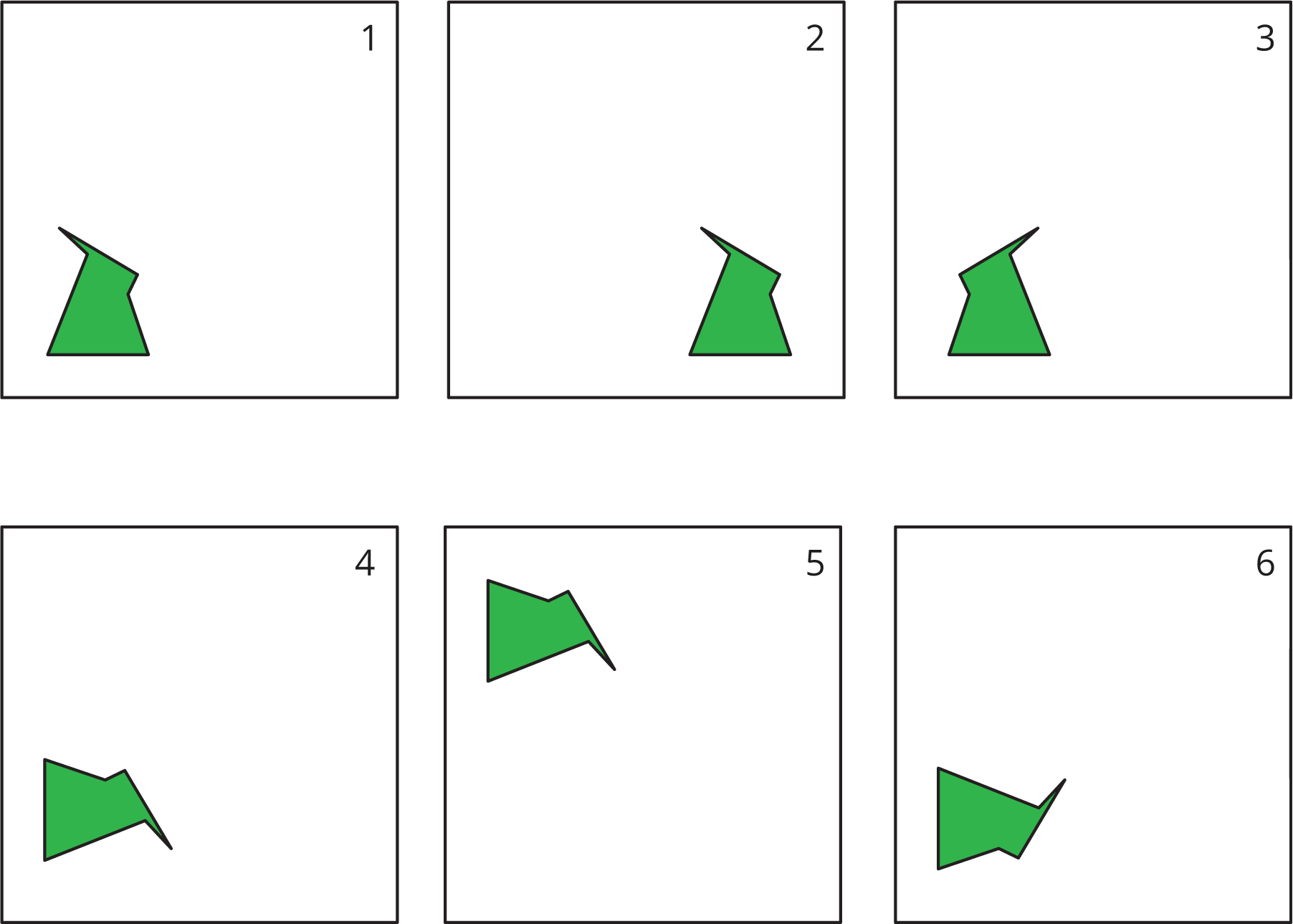
Describe each move or say if it is a new move.
Frame 1 to Frame 2.
Frame 2 to Frame 3.
Frame 3 to Frame 4.
Frame 4 to Frame 5.
How would you describe the new move?
Your teacher will give you a set of cards. Sort the cards into categories according to the type of move they show. Be prepared to describe each category and why it is different from the others. You can explore the applets below to see the ways the images move.
Drag the red point. Explore how the image changes.
Click on the box to show the transformed image.
Move the yellow points and the red segment to see how the image changes.
Here are the moves we have learned about so far:
A translation slides a figure without turning it. Every point in the figure goes the same distance in the same direction. For example, Figure A was translated down and to the left, as shown by the arrows. Figure B is a translation of Figure A.
A rotation turns a figure about a point, called the center of the rotation. Every point on the figure goes in a circle around the center and makes the same angle. The rotation can be clockwise, going in the same direction as the hands of a clock, or counterclockwise, going in the other direction. For example, Figure A was rotated 45^\circ clockwise around its bottom vertex. Figure C is a rotation of Figure A.

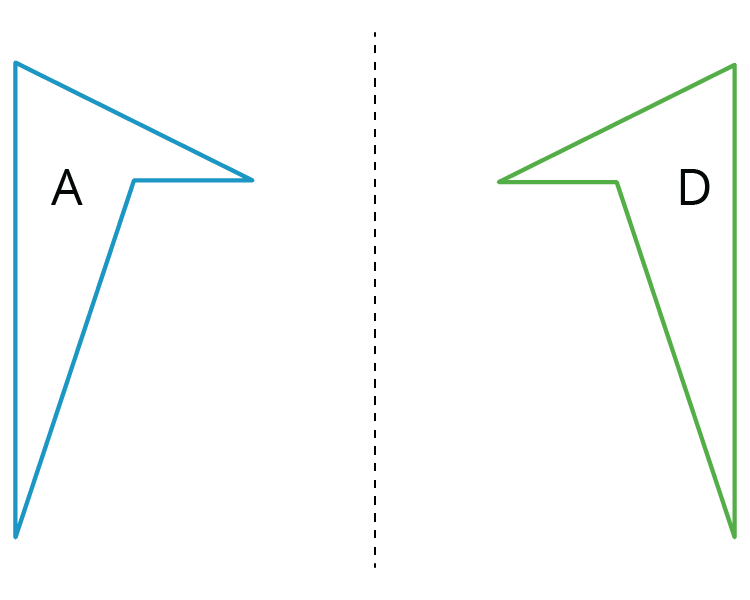
A reflection places points on the opposite side of a reflection line. The mirror image is a backwards copy of the original figure. The reflection line shows where the mirror should stand. For example, Figure A was reflected across the dotted line. Figure D is a reflection of Figure A.
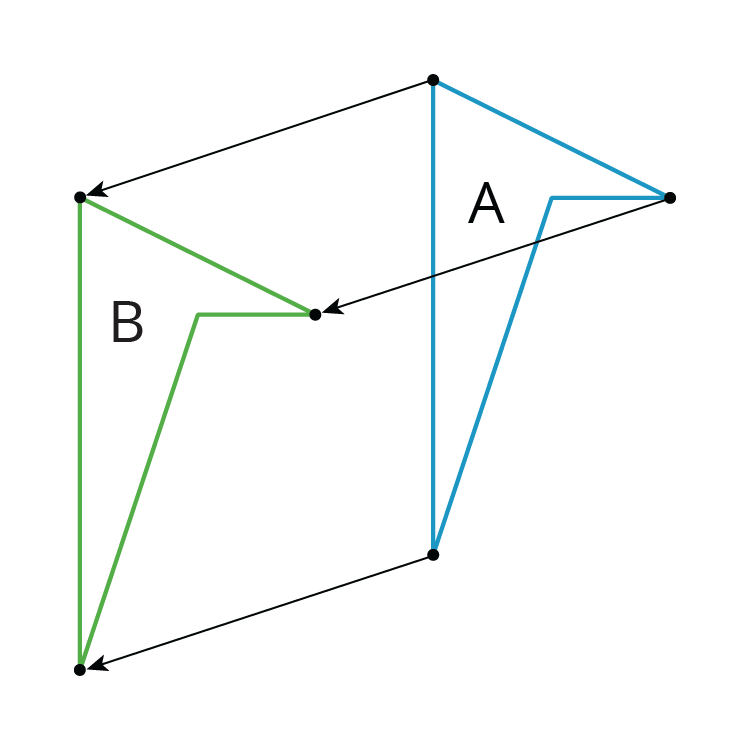
We use the word image to describe the new figure created by moving the original figure. If one point on the original figure moves to another point on the new figure, we call them corresponding points.
Translations, rotations, and reflections move objects in the plane. Points, segments, and other parts of the original all have corresponding parts on the “moved object.” The moved object is called the image.
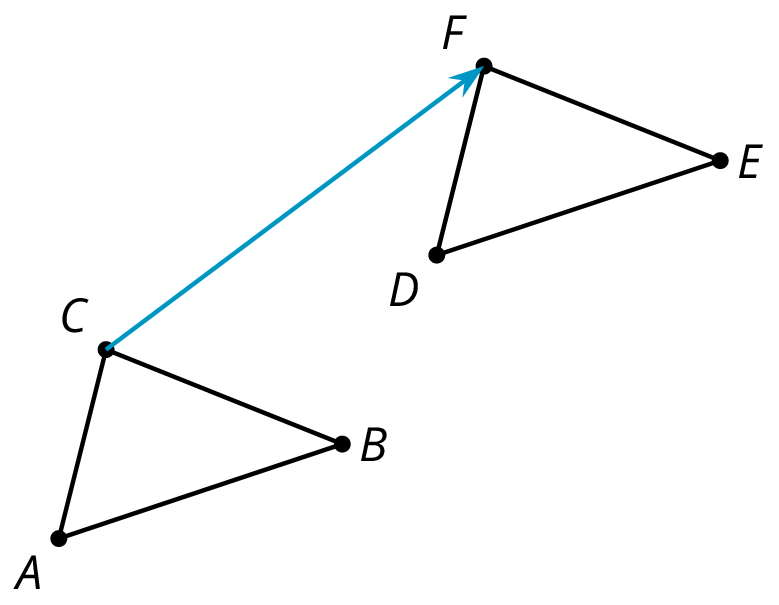
For example, here is triangle ABC and a translation to the right and up which is labeled DEF.
Point F in the image corresponds to point C, segment EF in the image corresponds to segment BD, and angle DEF corresponds to angle ABC.
If a part of the original figure matches up with a part of the copy, we call them corresponding parts. The part could be an angle, point, or side, and you can have corresponding angles, corresponding points, or corresponding sides.
If you have a distance between two points in the original figure, then the distance between the corresponding points in the copy is called the corresponding distance.
An object is rotating clockwise if it is turning in the same way that the hour or minute hand goes around a clock.
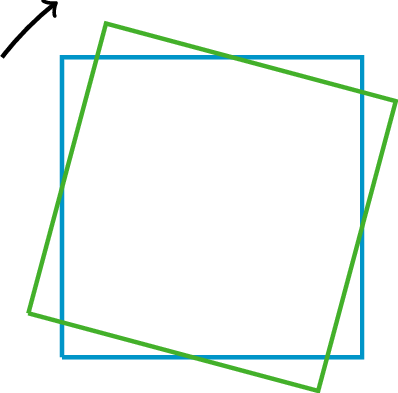
The tilted square is rotated 15^\circ clockwise from the square sitting horizontally on its base.
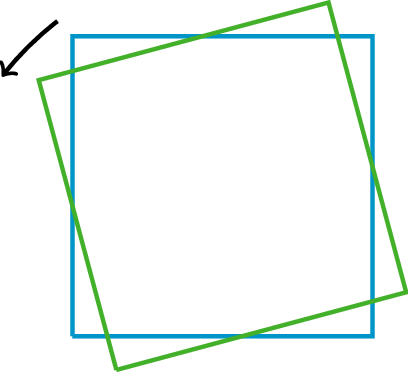
An object is rotating counterclockwise if it is turning in the opposite way to the way that the hour or minute hand goes around a clock.
The tilted square is rotated 15^\circ counterclockwise from the square with a horizontal base.
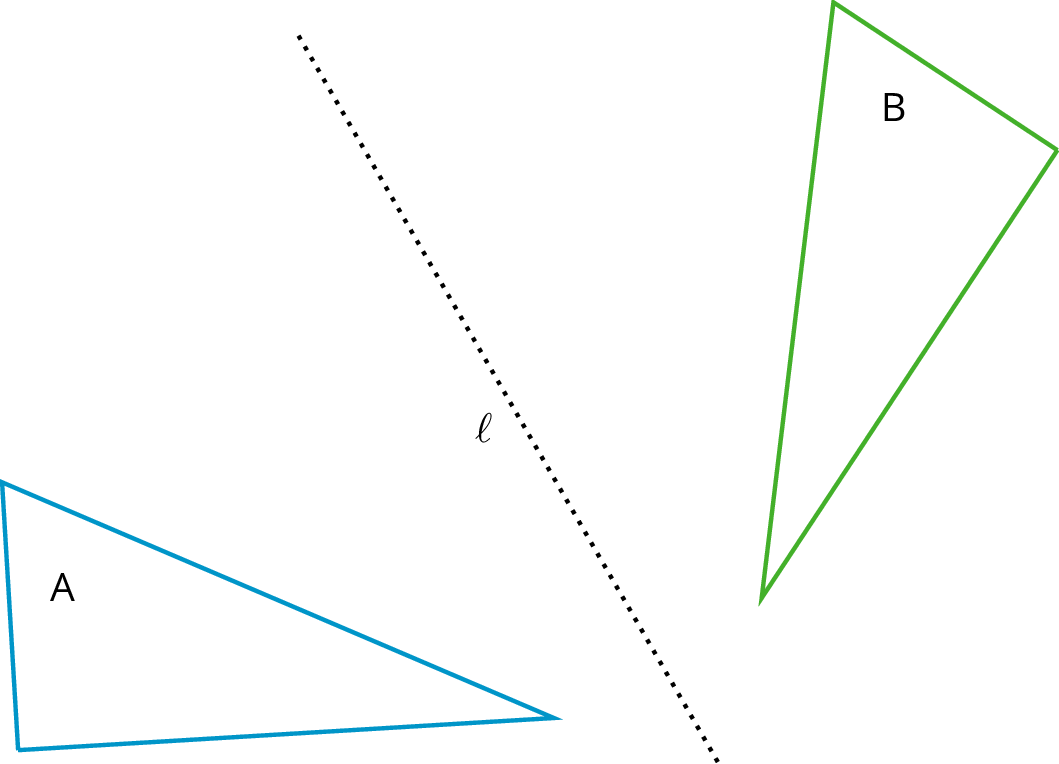
The reflection of a figure across a line takes every point of the figure to a point directly opposite to it on the other side of the line and the same distance from the line. In the figure, the triangle B is the reflection of the triangle A across the line \ell.
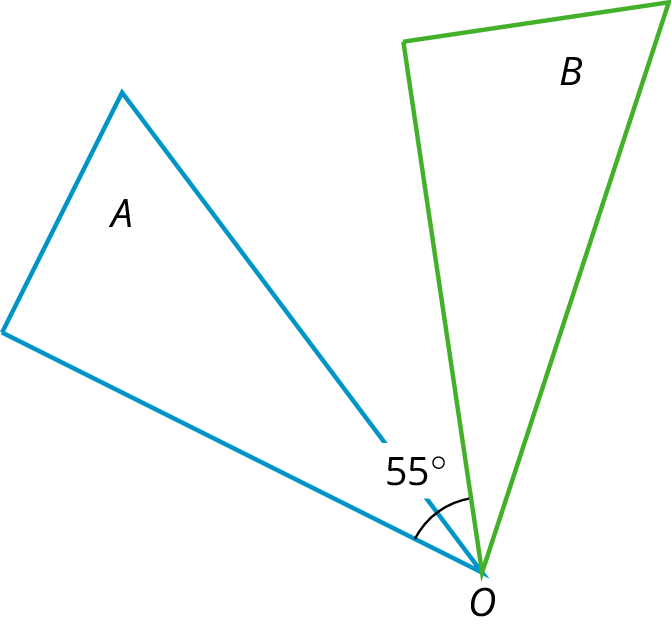
A rotation has a center, an angle, and a direction. It moves every point of a figure in a circle around the center, in the direction specified (clockwise or counterclockwise), and for a distance specified by the angle. For example, in the figure, triangle A is rotated 55^\circ clockwise about center O to get triangle B.
A translation has a distance and a direction. It moves every point in a figure the given distance in the given direction.
The figure on the left is translated to the figure on the right in the direction from A to B, using the distance from A to B.