Think about a sphere with radius r units that fits snugly inside a cylinder. The cylinder must then also have a radius of r units and a height of 2r units. Using what we have learned about volume, the cylinder has a volume of \pi r^2 h = \pi r^2 \boldcdot (2r), which is equal to 2\pi r^3 cubic units.
We know from an earlier lesson that the volume of a cone with the same base and height as a cylinder has \frac{1}{3} of the volume. In this example, such a cone has a volume of \frac{1}{3} \boldcdot \pi r^2 \boldcdot 2r or just \frac{2}{3} \pi r^3 cubic units.
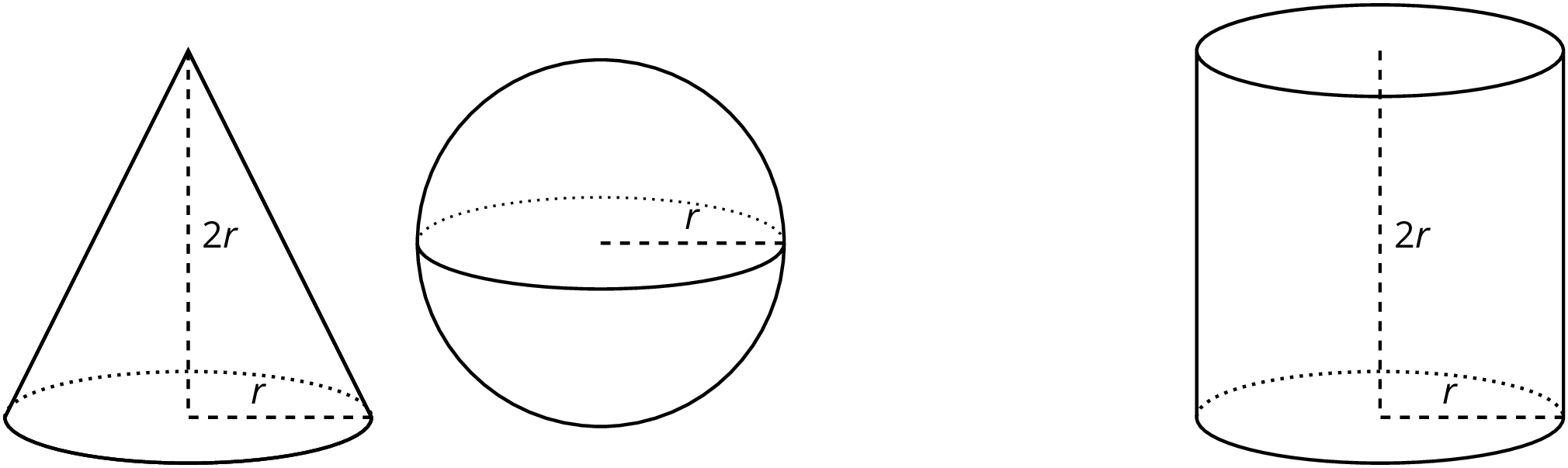
If we filled the cone and sphere with water, and then poured that water into the cylinder, the cylinder would be completely filled. That means the volume of the sphere and the volume of the cone add up to the volume of the cylinder. In other words, if V is the volume of the sphere, then
V +\frac{2}{3}\pi r^3= 2 \pi r^3
This leads to the formula for the volume of the sphere,
V = \frac{4}{3} \pi r^3