3.1: Points on a Ray
- Find and label a point C on the ray whose distance from A is twice the distance from B to A.
- Find and label a point D on the ray whose distance from A is half the distance from B to A.

Let’s dilate figures not on grids.

Dilate B using a scale factor of 5 and A as the center of dilation. Which point is its image?
Using H as the center of dilation, dilate G so that its image is E. What scale factor did you use?
Using H as the center of dilation, dilate E so that its image is G. What scale factor did you use?
To dilate F so that its image is B, what point on the diagram can you use as a center?
Dilate H using A as the center and a scale factor of \frac{1}{3}. Which point is its image?
Describe a dilation that uses a labeled point as its center and that would take F to H.
Using B as the center of dilation, dilate H so that its image is itself. What scale factor did you use?
Follow the directions to perform the dilations in the applet.

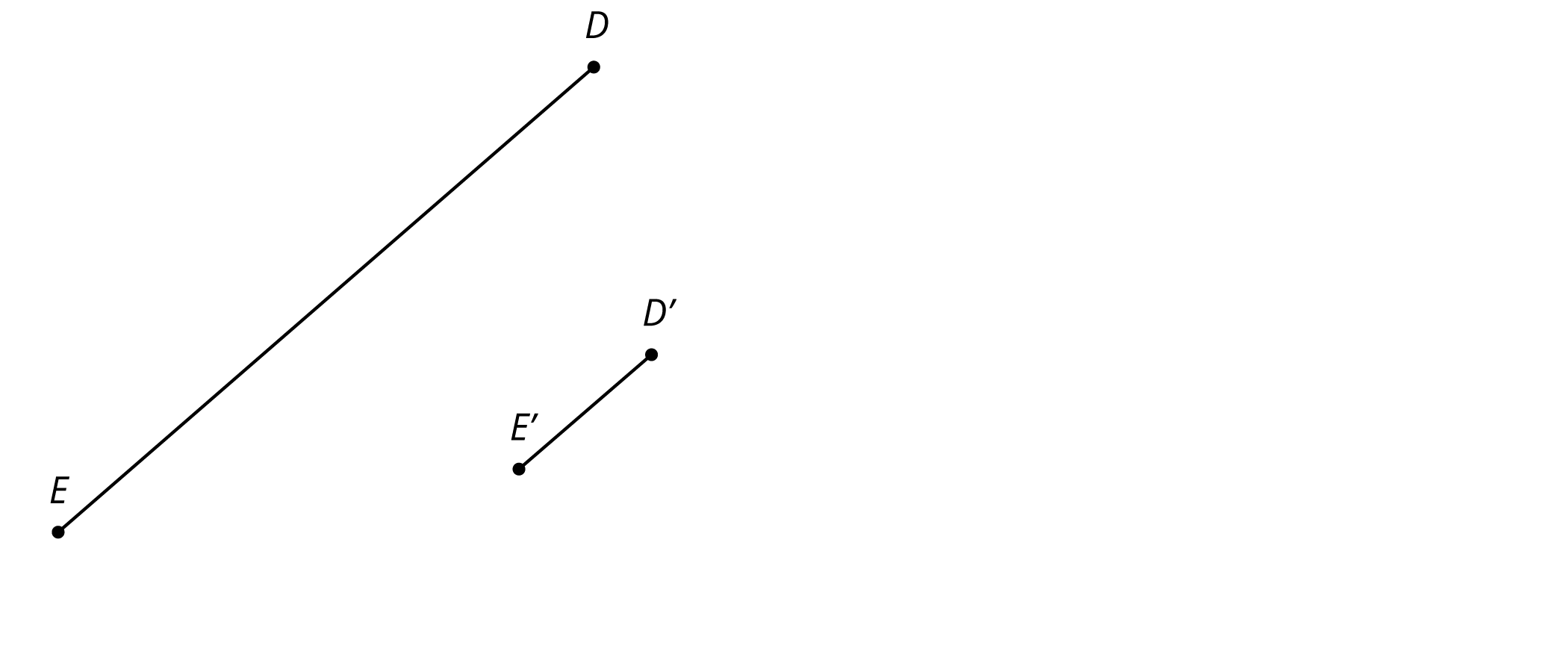
Here is line segment DE and its image D’E’ under a dilation.
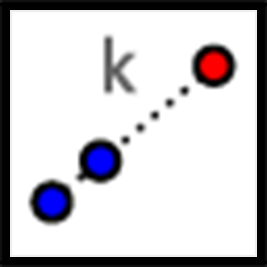
If A is the center of dilation, how can we find which point is the dilation of B with scale factor 2?
 Since the scale factor is larger than 1, the point must be farther away from A than B is, which makes C the point we are looking for. If we measure the distance between A and C, we would find that it is exactly twice the distance between A and B.
Since the scale factor is larger than 1, the point must be farther away from A than B is, which makes C the point we are looking for. If we measure the distance between A and C, we would find that it is exactly twice the distance between A and B.
A dilation with scale factor less than 1 brings points closer. The point D is the dilation of B with center A and scale factor \frac{1}{3}.