11.1: Which One Doesn’t Belong: Bases and Heights
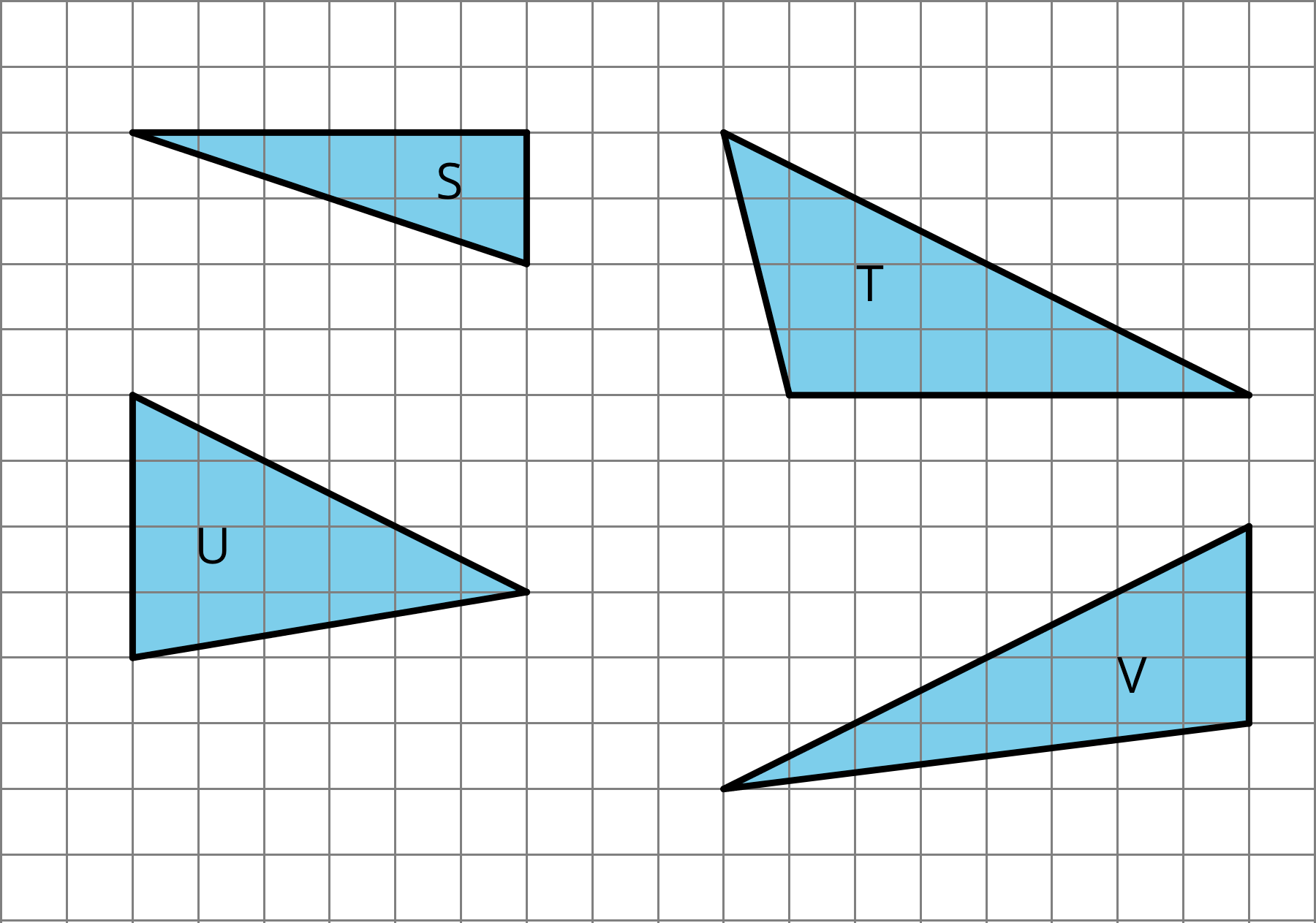
Which one doesn't belong?
Let’s investigate polygons and their areas.
Which one doesn't belong?

Here are five polygons:

Here are six figures that are not polygons:
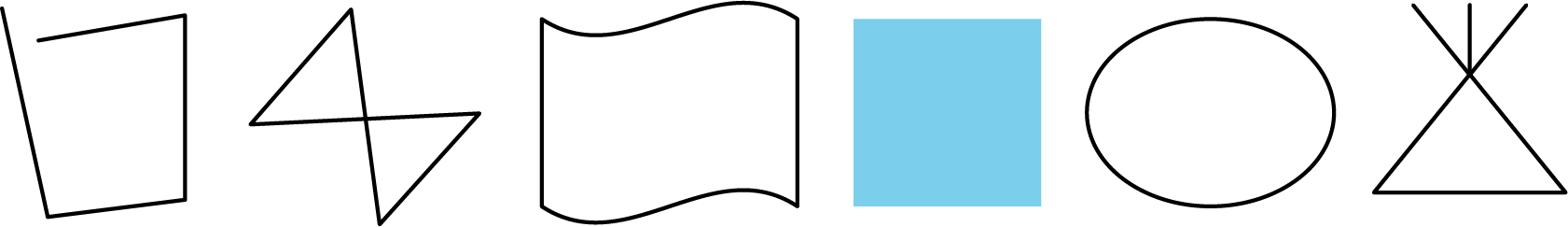
Circle the figures that are polygons.
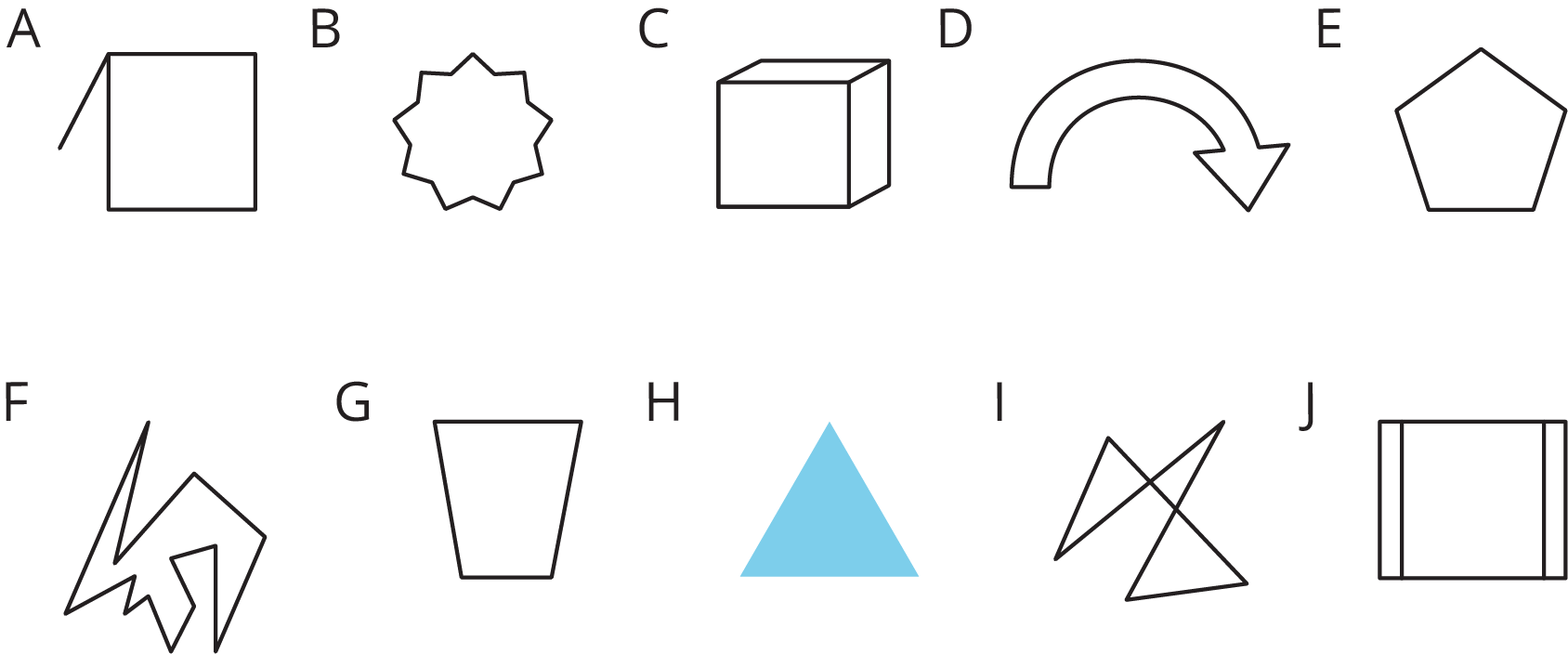
What do the figures you circled have in common? What characteristics helped you decide whether a figure was a polygon?
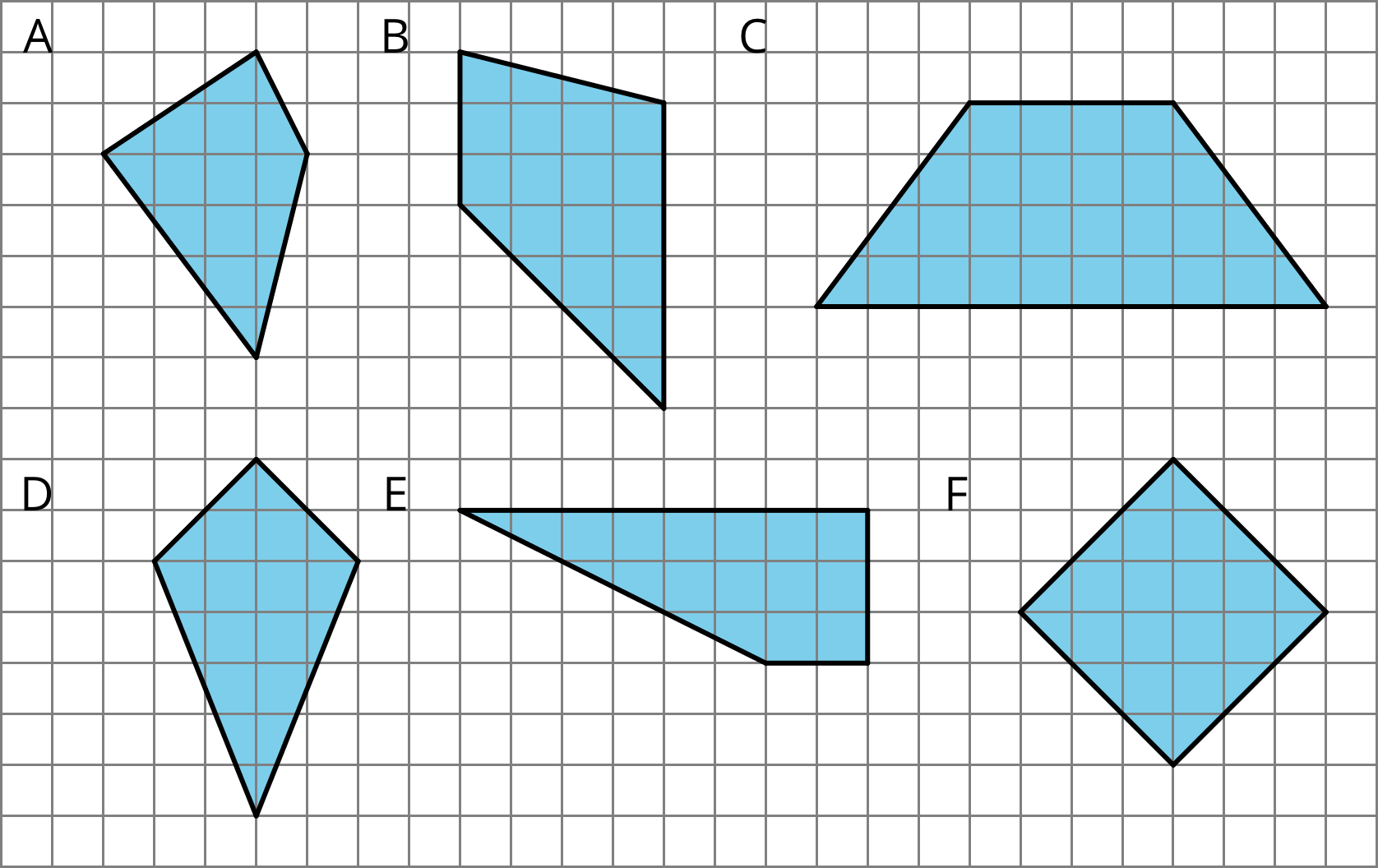
Find the area of two quadrilaterals of your choice. Show your reasoning.
Here is a trapezoid. a and b represent the lengths of its bottom and top sides. The segment labeled h represents its height; it is perpendicular to both the top and bottom sides.
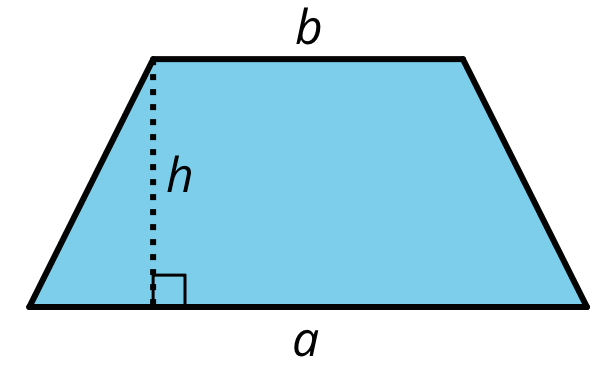
Apply area-reasoning strategies—decomposing, rearranging, duplicating, etc.—on the trapezoid so that you have one or more shapes with areas that you already know how to find.
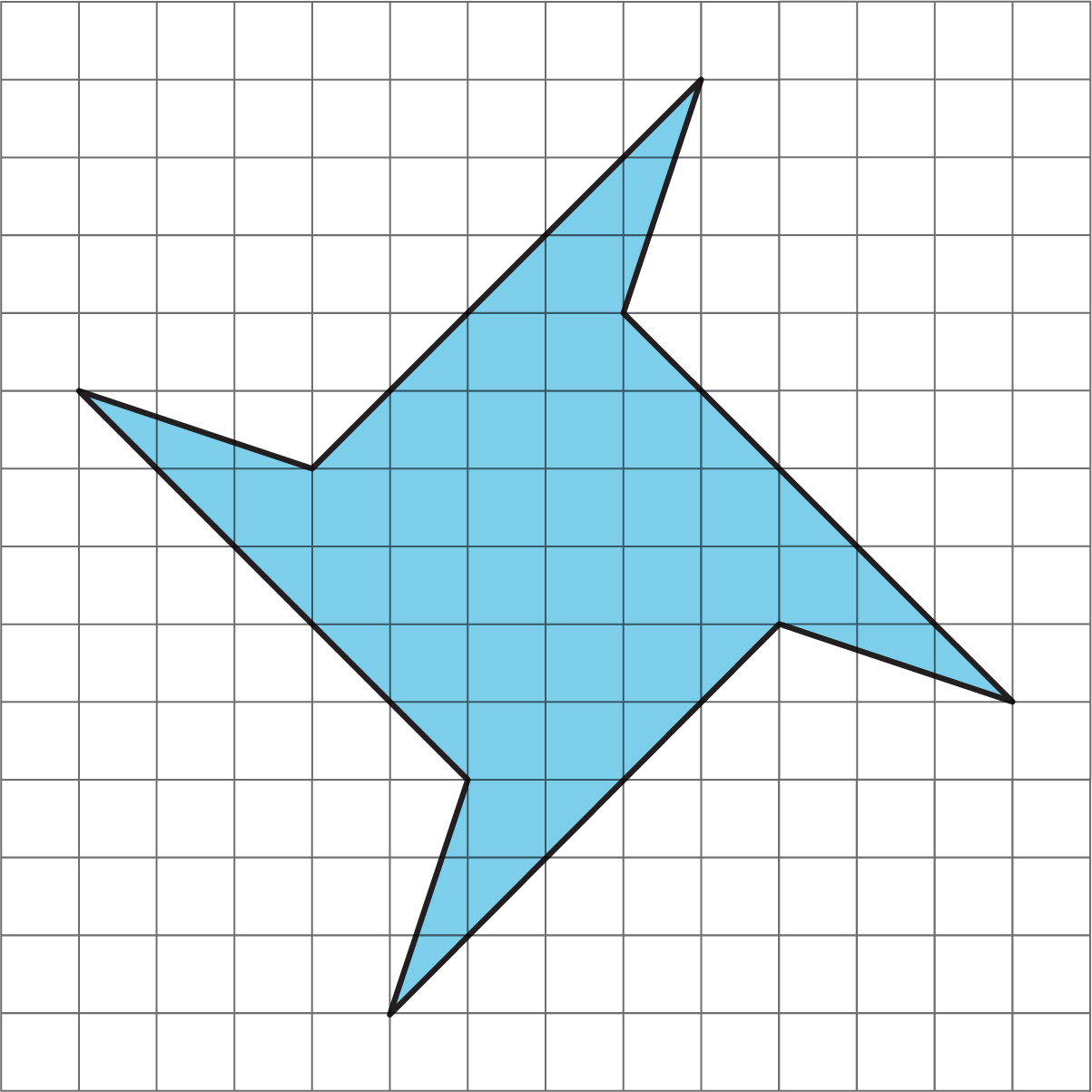
Find the area of the shaded region in square units. Show your reasoning.
A polygon is a two-dimensional figure composed of straight line segments.
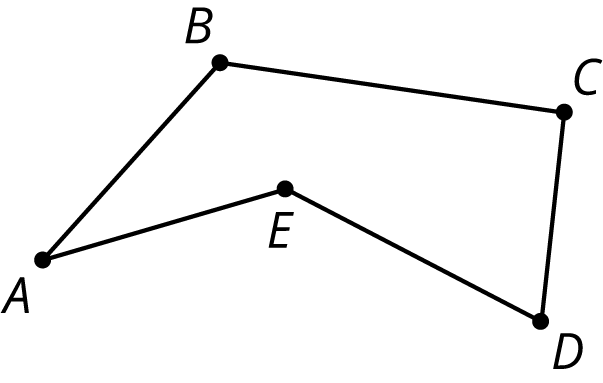
Here is a polygon with 5 sides. The vertices are labeled A, B, C, D, and E.
A polygon encloses a region. To find the area of a polygon is to find the area of the region inside it.
We can find the area of a polygon by decomposing the region inside it into triangles and rectangles.

The first two diagrams show the polygon decomposed into triangles and rectangles; the sum of their areas is the area of the polygon. The last diagram shows the polygon enclosed with a rectangle; subtracting the areas of the triangles from the area of the rectangle gives us the area of the polygon.
A quadrilateral is a four-sided polygon.
A vertex is a point where two edges meet in a polygon or a polyhedron.
A line segment in a polygon is called an edge (it is also called a side). A line segment where two faces meet in a polyhedron is also called an edge.
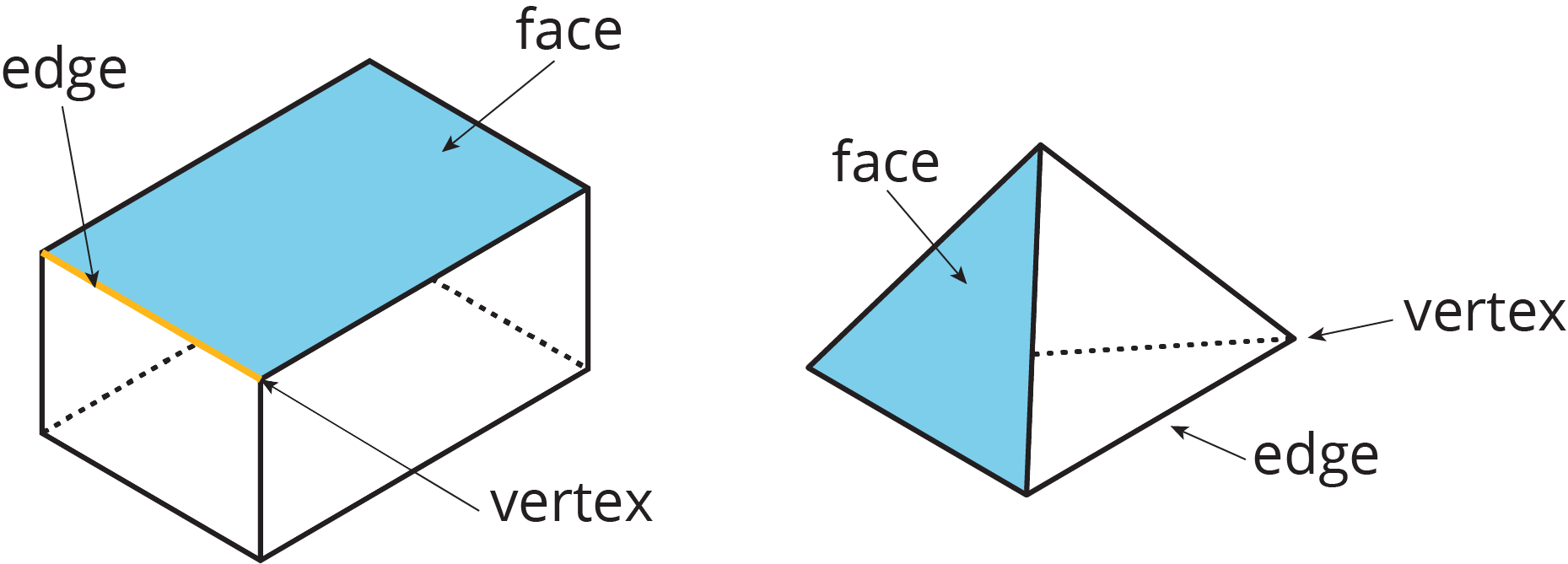
A line segment in a polygon is called a side (it is also called an edge).
Sometimes the faces of a polyhedron are called its sides.
A polygon is a two-dimensional figure composed of a sequence of straight line segments, connected end-to-end, with the last one connecting back to the first. We call the line segments the edges or sides of the polygon. We call a point where the edges connect a vertex. The edges of a polygon never cross each other.
The plural of vertex is vertices. A polygon always encloses a two-dimensional region.
Here is a polygon with five vertices A, B, C, D, and E and five edges (or sides): \overline{AB}, \overline{BC}, \overline{CD}, \overline{DE}, and \overline{EA}.
