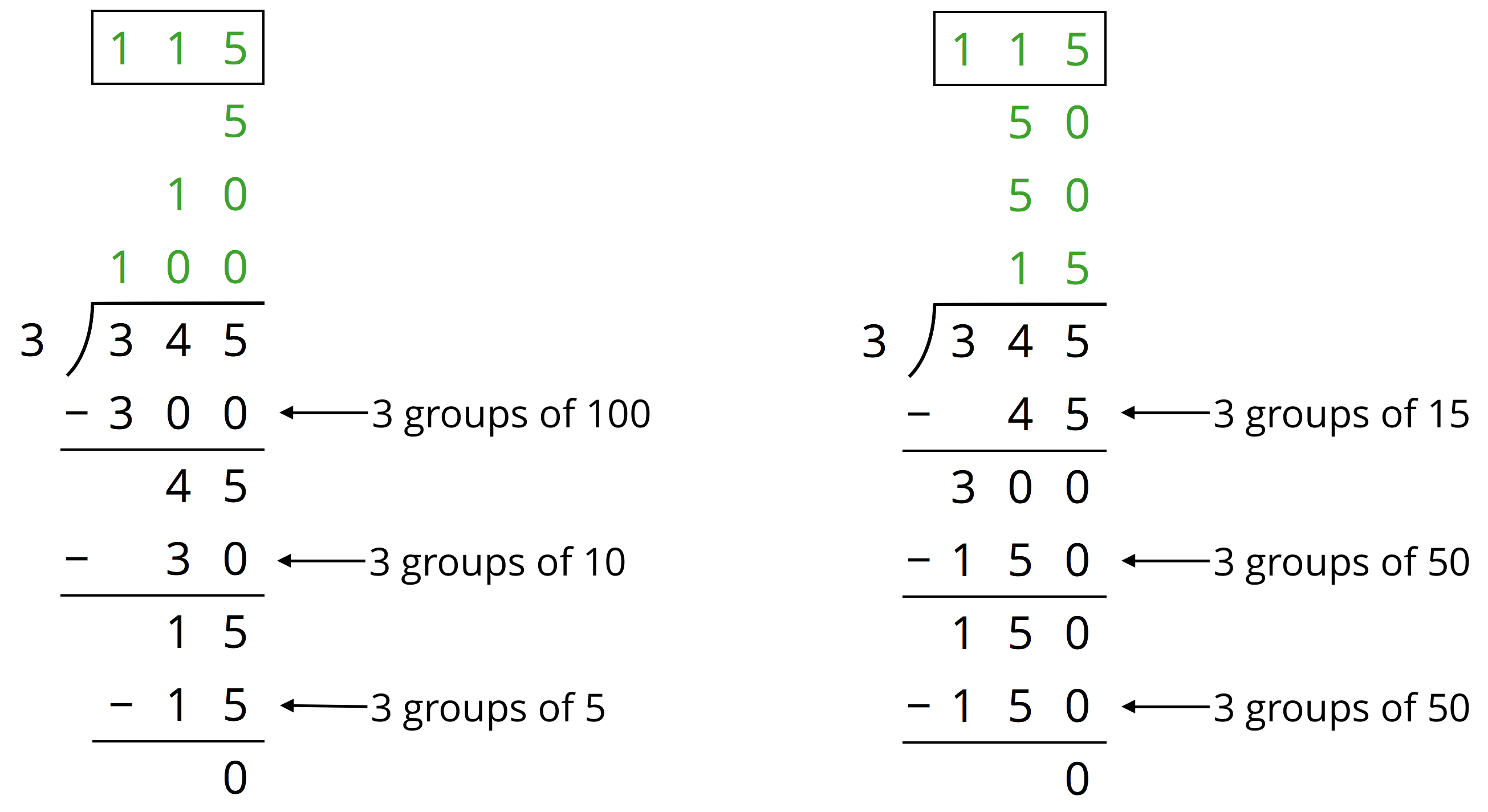Lesson 9: Using the Partial Quotients Method

Let’s divide whole numbers.

9.1: Using Base-Ten Diagrams to Calculate Quotients

Elena used base-ten diagrams to find 372 \div 3. She started by representing 372.

She made 3 groups, each with 1 hundred. Then, she put the tens and ones in each of the 3 groups. Here is her diagram for 372 \div 3.

Discuss with a partner:

  • Elena’s diagram for 372 has 7 tens. The one for 372 \div 3 has only 6 tens. Why?
  • Where did the extra ones (small squares) come from?

9.2: Using the Partial Quotients Method to Calculate Quotients

  1. Andre calculated 657 \div 3 using a method that was different from Elena’s.

    Discuss the following questions with a partner:

    • Andre subtracted 600 from 657. What does the 600 represent?
    • Andre wrote 10 above the 200, and then subtracted 30 from 57. How is the 30 related to the 10?
    • What do the numbers 200, 10, and 9 represent?
    • What is the meaning of the 0 at the bottom of Andre’s work?

  2. How might Andre calculate 896 \div 4? Explain or show your reasoning.

9.3: What’s the Quotient?

  1. Find the quotient of 1,\!332 \div 9 using one of the methods you have seen so far. Show your reasoning.

  2. Find each quotient and show your reasoning. Use the partial quotients method at least once.

    1. 1,\!115 \div 5
    1. 665 \div 7
    1. 432 \div 16

Summary

We can find the quotient 345\div 3 in different ways.

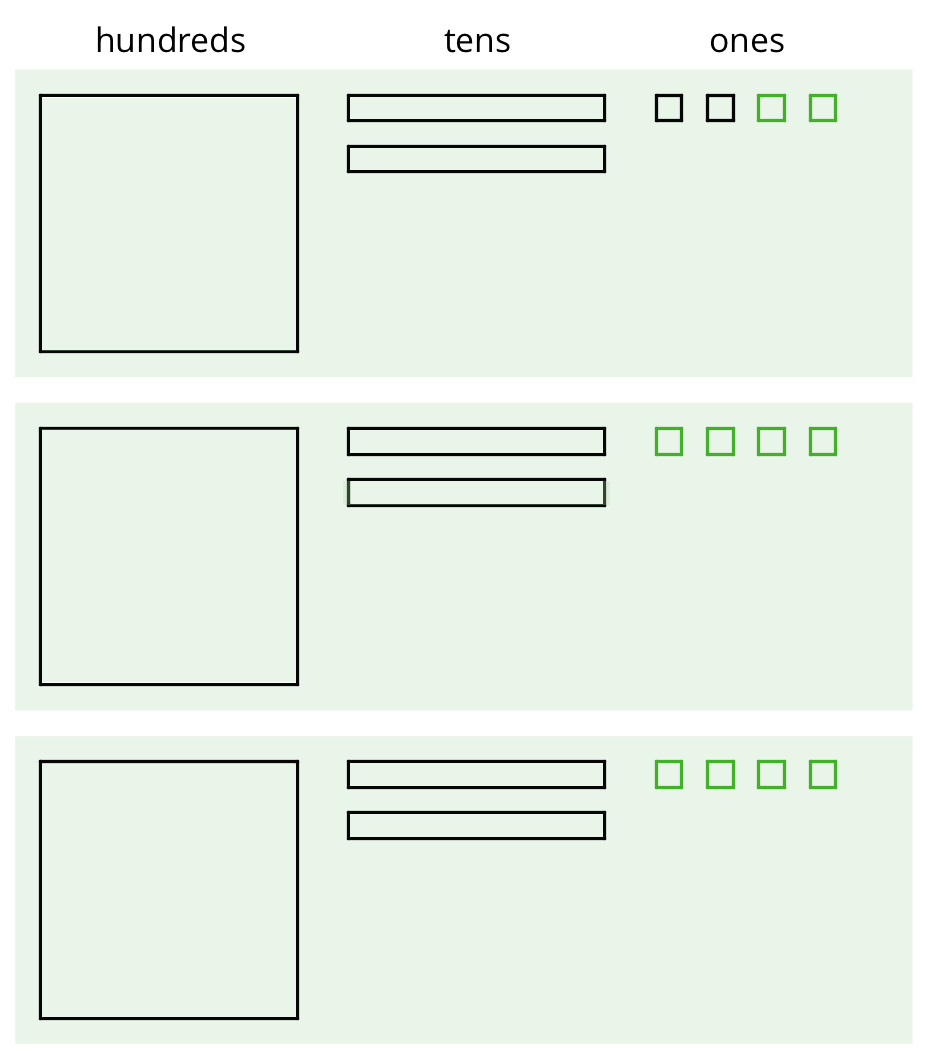
One way is to use a base-ten diagram to represent the hundreds, tens, and ones and to create equal-sized groups. 

We can think of the division by 3 as splitting up 345 into 3 equal groups.

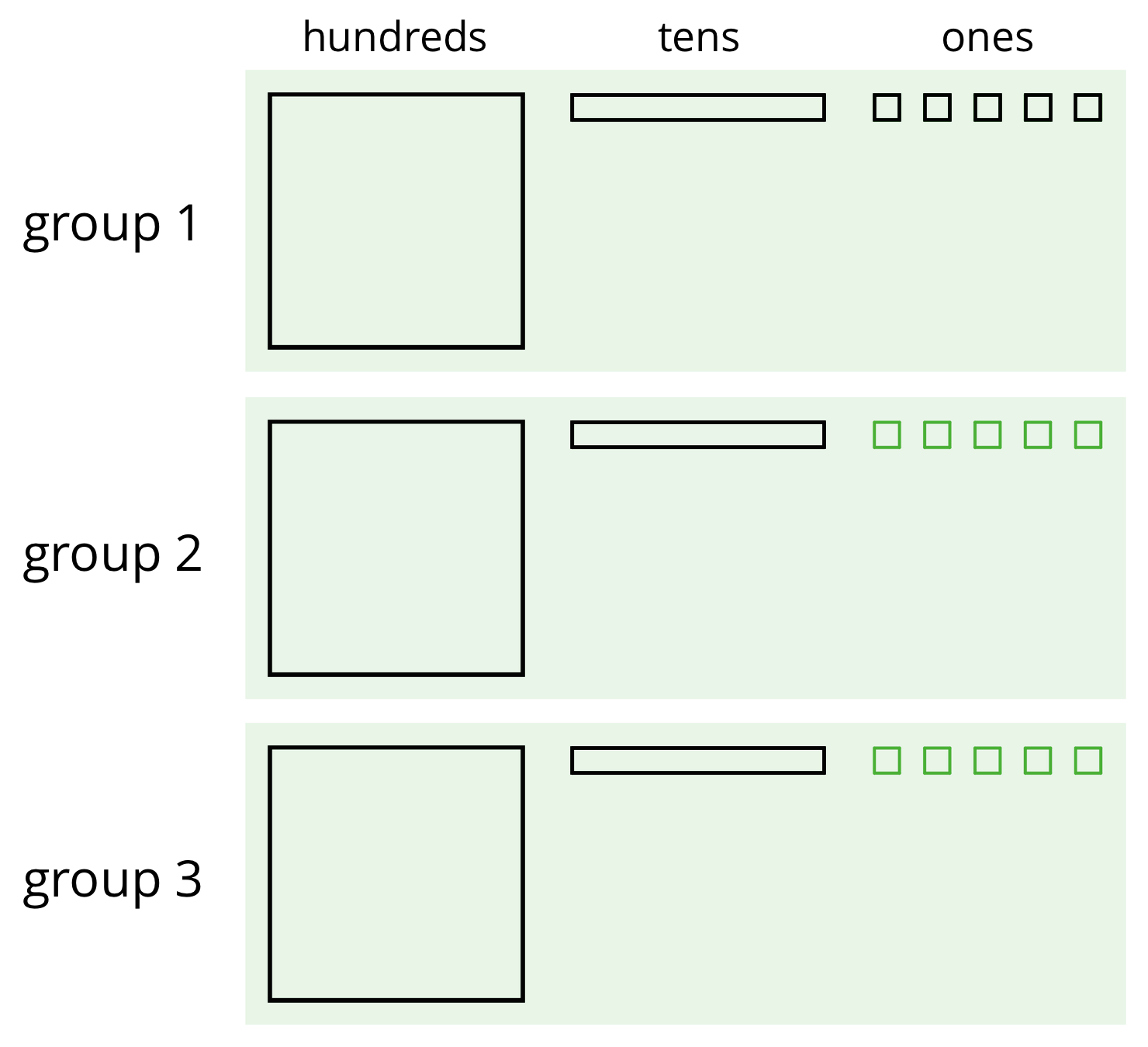
Each group has 1 hundred, 1 ten, and 5 ones, so 345 \div 3 = 115. Notice that in order to split 345 into 3 equal groups, one of the tens had to be unbundled or decomposed into 10 ones.

Another way to divide 345 by 3 is by using the partial quotients method, in which we keep subtracting 3 groups of some amount from 345.  

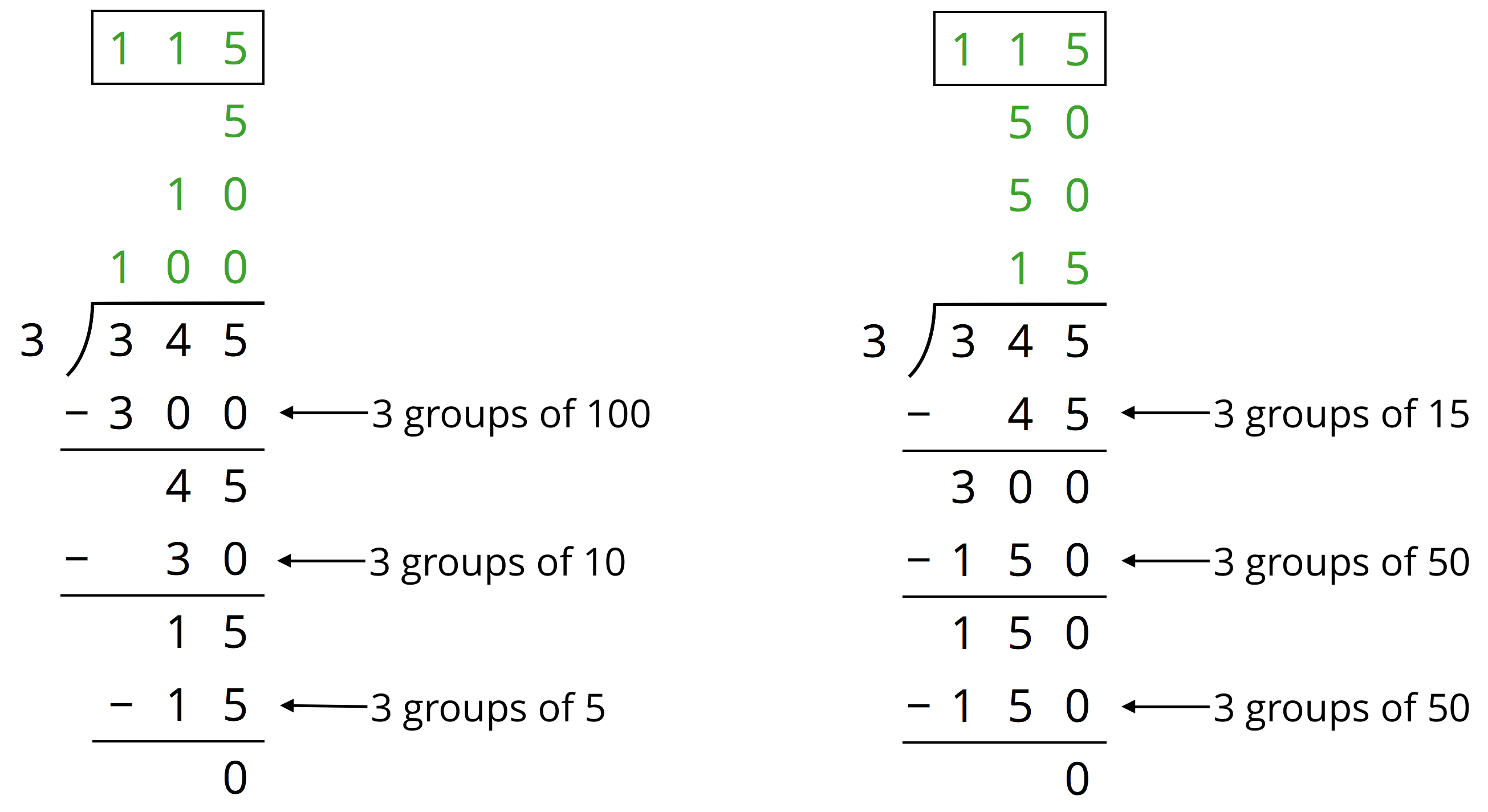
  • In the calculation on the left, first we subtract 3 groups of 100, then 3 groups of 10, and then 3 groups of 5. Adding up the partial quotients (100+10+5) gives us 115.
  • The calculation on the right shows a different amount per group subtracted each time (3 groups of 15, 3 groups of 50, and 3 more groups of 50), but the total amount in each of the 3 groups is still 115. There are other ways of calculating 345 \div 3 using the partial quotients method. 

Both the base-ten diagrams and partial quotients methods are effective. If, however, the dividend and divisor are large, as in 1,\!248 \div 26, then the base-ten diagrams will be time-consuming.

Practice Problems ▶