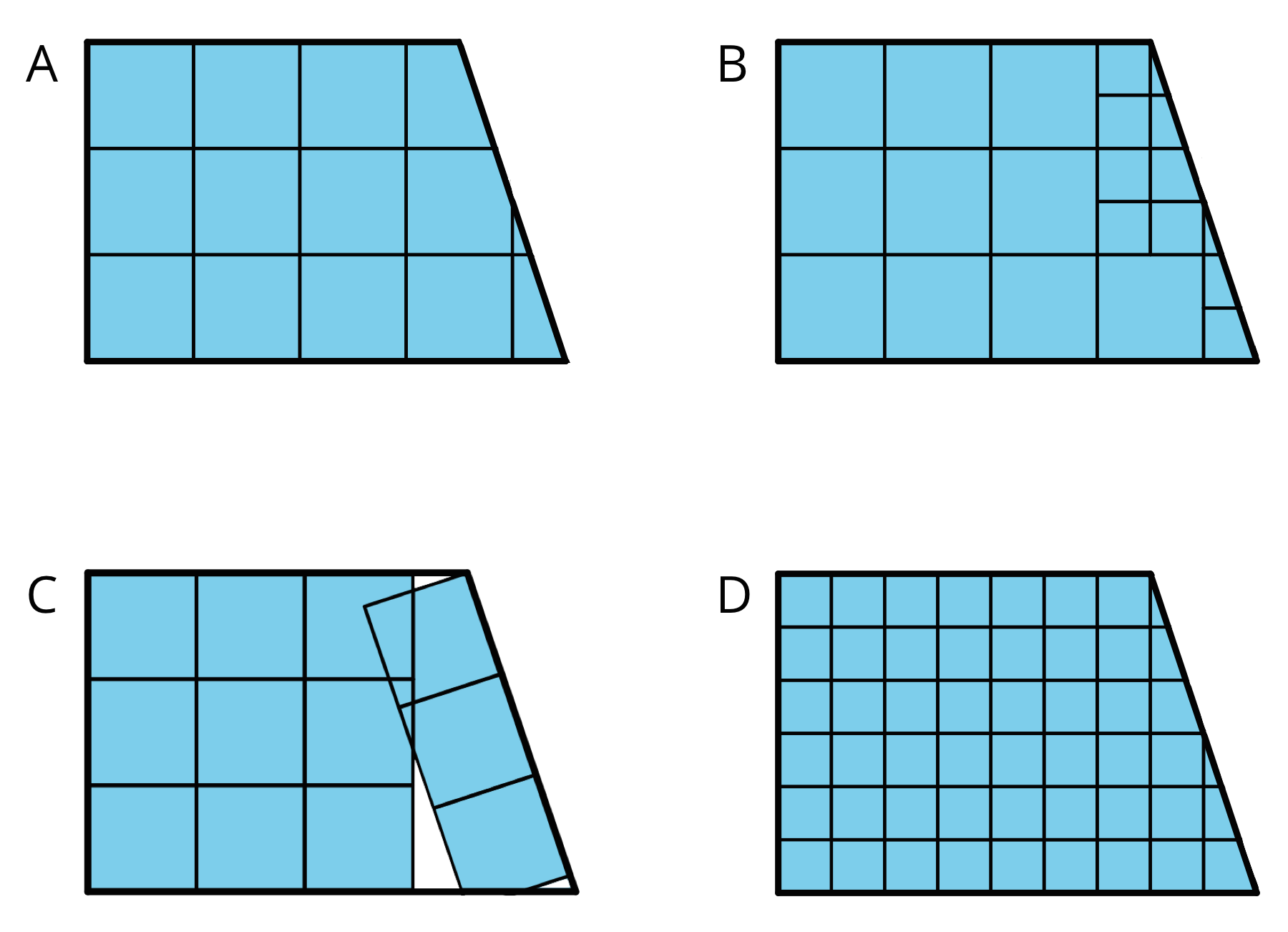
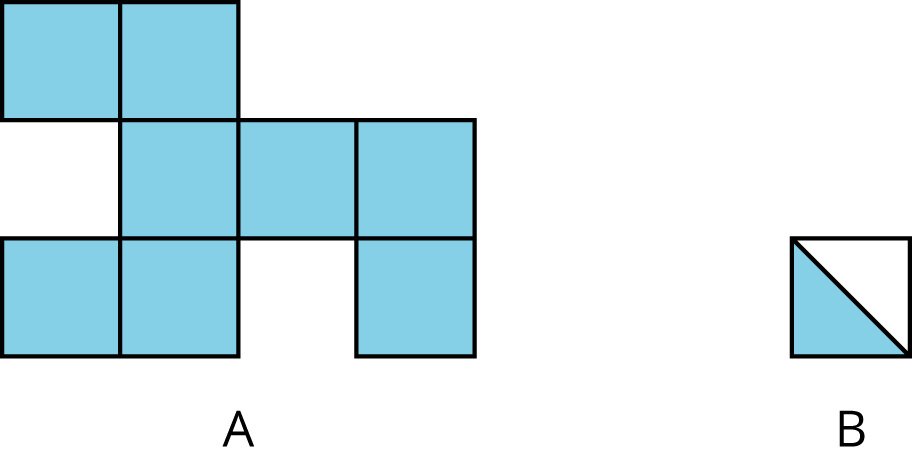Lesson 2: Finding Area by Decomposing and Rearranging

Let’s create shapes and find their areas.

2.1: What is Area?

You may recall that the term area tells us something about the number of squares inside a two-dimensional shape.

  1. Here are four drawings that each show squares inside a shape. Select all drawings whose squares could be used to find the area of the shape. Be prepared to explain your reasoning.

    An image of four shapes labeled A, B, C, and D. Shape A is broken up into large squares, Shape B is broken up into a combination of large and small squares, Shape C is broken up into a combination of large squares and white space, and Shape D is broken up into small squares.

  2. Write a definition of area that includes all the information that you think is important. 

2.2: Composing Shapes

This applet has one square and some small, medium, and large right triangles. The area of the square is 1 square unit.

Click on a shape and drag to move it. Grab the point at the vertex and drag to turn it.

  1. Notice that you can put together two small triangles to make a square. What is the area of the square composed of two small triangles? Be prepared to explain your reasoning.

GeoGebra Applet PHTsMPDY

  1. Use your shapes to create a new shape with an area of 1 square unit that is not a square. Draw your shape on paper and label it with its area.

  2. Use your shapes to create a new shape with an area of 2 square units. Draw your shape and label it with its area.

  3. Use your shapes to create a different shape with an area of 2 square units. Draw your shape and label it with its area.

  4. Use your shapes to create a new shape with an area of 4 square units. Draw your shape and label it with its area.

2.3: Tangram Triangles

Recall that the area of the square you saw earlier is 1 square unit. Complete each statement and explain your reasoning.

  1. The area of the small triangle is ____________ square units. I know this because . . .
  2. The area of the medium triangle is ____________ square units. I know this because . . .
  3. The area of the large triangle is ____________ square units. I know this because . . .

GeoGebra Applet J4f6V5NE

Summary

Here are two important principles for finding area:

  1. If two figures can be placed one on top of the other so that they match up exactly, then they have the same area.

  2. We can decompose a figure (break a figure into pieces) and rearrange the pieces (move the pieces around) to find its area.

Here are illustrations of the two principles.

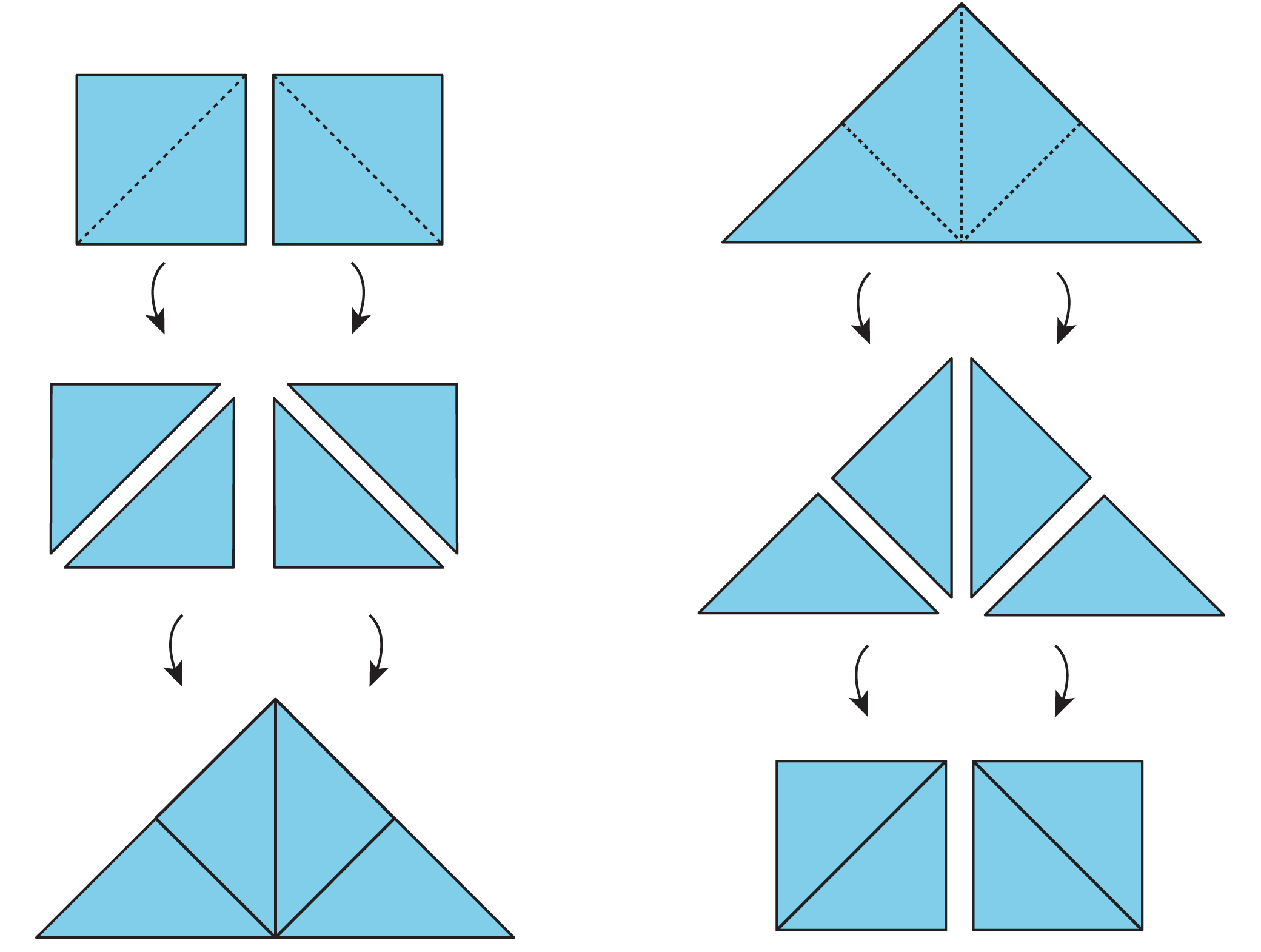
An image of two squares, which are then decomposed into four triangles, which are then rearranged into one large triangle. Another image of a large triangle that is decomposed into four smaller triangles, and then rearranged into two squares.​
  • Each square on the left can be decomposed into 2 triangles. These triangles can be rearranged into a large triangle. So the large triangle has the same area as the 2 squares.

  • Similarly, the large triangle on the right can be decomposed into 4 equal triangles. The triangles can be rearranged to form 2 squares. If each square has an area of 1 square unit, then the area of the large triangle is 2 square units. We also can say that each small triangle has an area of $\frac12$ square unit.

Practice Problems ▶

Glossary

area

area

The area of a two-dimensional region, measured in square units, is the number of unit squares that cover the region without gaps or overlaps.

The side length of each square is 1 centimeter. The area of the shaded region A is 8 square centimeters. The area of shaded region B is $\frac12$ square centimeters.

rearrange

rearrange

When we decompose a figure into pieces and put them back together in a different way, we are rearranging the pieces.

compose/decompose

compose/decompose

Compose means “put together” and decompose means “take apart.” We use the word “compose” to describe putting several geometric figures together to make a new figure.