A box plot represents the five-number summary of a data set.
It shows the first quartile (Q1) and the third quartile (Q3) as the left and right sides of a rectangle or a box. The median (Q2) is shown as a vertical segment inside the box. On the left side, a horizontal line segment—a “whisker”—extends from Q1 to the minimum value. On the right, a whisker extends from Q3 to the maximum value.
The rectangle in the middle represents the middle half of the data. Its width is the IQR. The whiskers represent the bottom quarter and top quarter of the data set.
Earlier we saw dot plots representing the weights of pugs and beagles. The box plots for these data sets are shown above the corresponding dot plots.
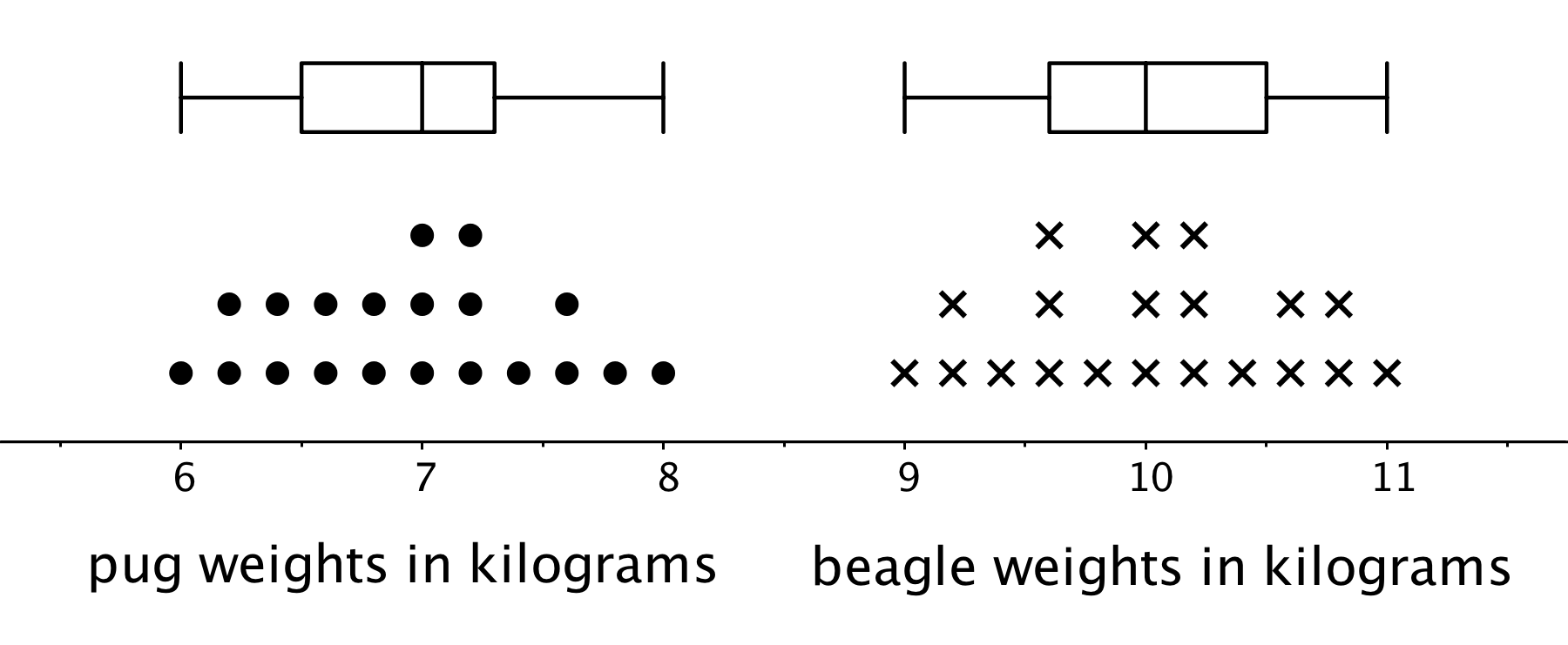
We can tell from the box plots that, in general, the pugs in the group are lighter than the beagles: the median weight of pugs is 7 kilograms and the median weight of beagles is 10 kilograms. Because the two box plots are on the same scale and the rectangles have similar widths, we can also tell that the IQRs for the two breeds are very similar. This suggests that the variability in the beagle weights is very similar to the variability in the pug weights.

