Lesson 7: Using Histograms to Answer Statistical Questions

Let's draw histograms and use them to answer questions.

7.1: Which One Doesn’t Belong: Questions

Here are four questions about the population of Alaska. Which question does not belong? Be prepared to explain your reasoning.

  1. In general, at what age do Alaska residents retire?

  2. At what age can Alaskans vote?
  1. What is the age difference between the youngest and oldest Alaska residents with a full-time job?
  2. Which age group is the largest part of the population: 18 years or younger, 19–25 years, 25–34 years, 35–44 years, 45–54 years, 55–64 years, or 65 years or older?

7.2: Measuring Earthworms

An earthworm farmer set up several containers of a certain species of earthworms so that he could learn about their lengths. The lengths of the earthworms provide information about their ages. The farmer measured the lengths of 25 earthworms in one of the containers. Each length was measured in millimeters.

Earthworm Copyright Owner: JKpics License: Public Domain Via: Pixabay

  1. Using a ruler, draw a line segment for each length:

    • 20 millimeters

    • 40 millimeters

    • 60 millimeters

    • 80 millimeters

    • 100 millimeters

    1. Here are the lengths, in millimeters, of the 25 earthworms.

      6 11 18 19 20 23 23 25 25 26
      27 27 28 29 32 33 41 42 48 52
      54 59 60 77 93          

      Complete the table for the lengths of the 25 earthworms.

      Row 1 length frequency
      Row 2 0 millimeters to less than 20 millimeters  
      Row 3 20 millimeters to less than 40 millimeters  
      Row 4 40 millimeters to less than 60 millimeters  
      Row 5 60 millimeters to less than 80 millimeters  
      Row 6 80 millimeters to less than 100 millimeters  

  2. Use the grid and the information in the table to draw a histogram for the worm length data. Be sure to label the axes of your histogram.

    A blank grid: The horizontal axis has the numbers 0 through 100, in increments of 10, indicated. The vertical axis has the numbers 0 through 14, in increments of 2, indicated and there are horizontal lines midway between the indicated numbers.
  3. Based on the histogram, what is a typical length for these 25 earthworms? Explain how you know.
  4. Write 1–2 sentences to describe the spread of the data. Do most of the worms have a length that is close to your estimate of a typical length, or are they very different in length?

7.3: Tall and Taller Players

Professional basketball players tend to be taller than professional baseball players.

Here are two histograms that show height distributions of 50 male professional baseball players and 50 male professional basketball players.

  1. Decide which histogram shows the heights of baseball players and which shows the heights of basketball players. Be prepared to explain your reasoning.

    Two histograms: Labeled A and B. On each histogram, the horizontal axes are labeled “height in inches” and the numbers 66 through 90, in increments of 2, are indicated. On the vertical axes, the numbers 0 through 20, in increments of 4, are indicated. The data for histogram A are as follows: Length from 66 up to 68, 0. Length from 68 up to 70, 0. Length from 70 up to 72, 1. Length from 72 up to 74, 0. Length from 74 up to 76, 5. Length from 76 up to 78, 14. Length from 78 up to 80, 10. Length from 80 up to 82, 14. Length from 82 up to 84, 5. Length from 84 up to 86, 2. Length from 86 up to 88, 0. Length from 88 up to 90, 1. The data for histogram B are as follows: Length from 66 up to 68, 2. Length from 68 up to 70, 3. Length from 70 up to 72, 14. Length from 72 up to 74, 19. Length from 74 up to 76, 6. Length from 76 up to 78, 4. Length from 78 up to 80, 1. Length from 80 up to 82, 0. Length from 82 up to 84, 0. Length from 84 up to 86, 0. Length from 86 up to 88, 0. Length from 88 up to 90, 0.

  2. Write 2–3 sentences that describe the distribution of the heights of the basketball players. Comment on the center and spread of the data.
  3. Write 2–3 sentences that describe the distribution of the heights of the baseball players. Comment on the center and spread of the data.

Summary

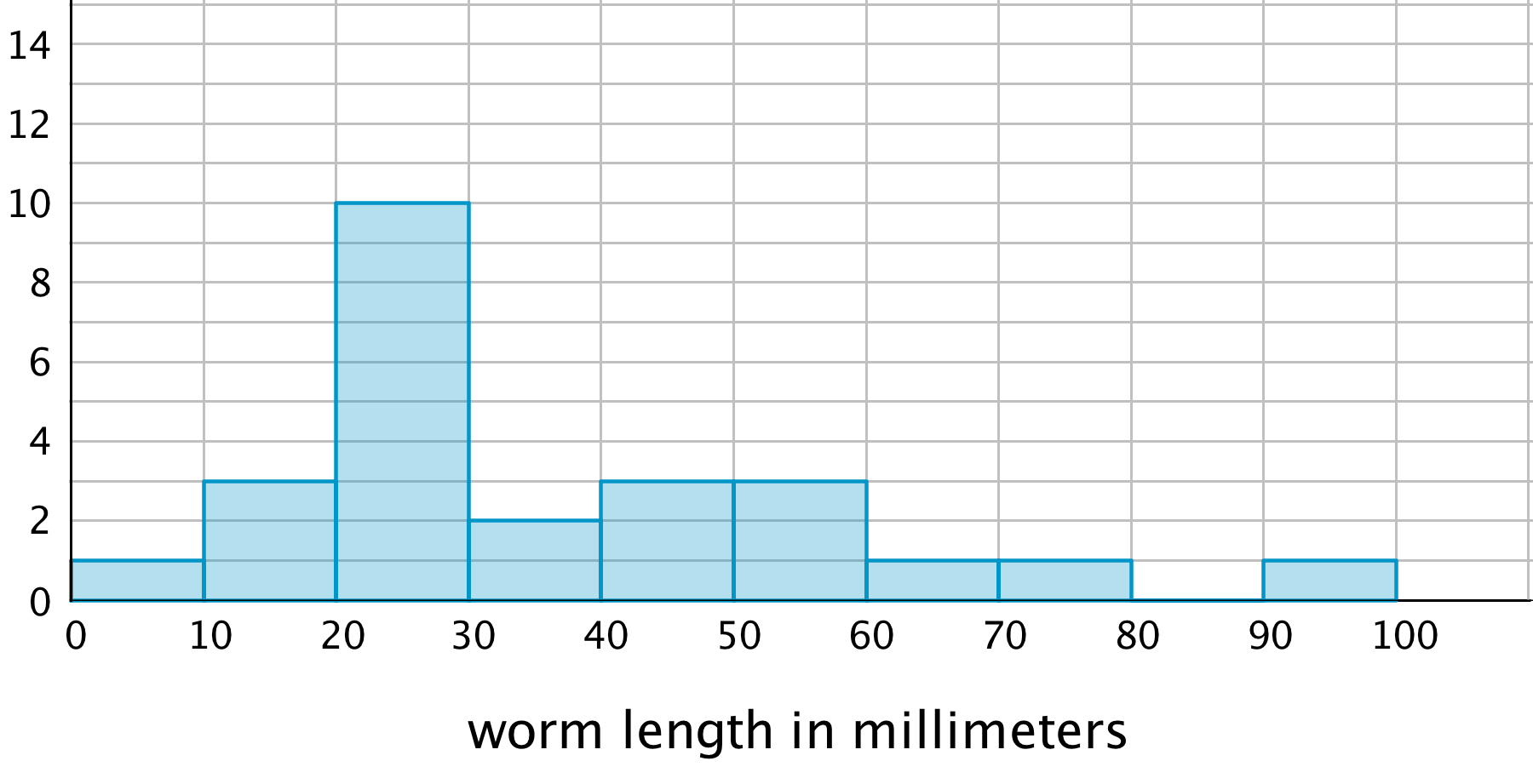
Here are the weights, in kilograms, of 30 dogs.

10 11 12 12 13 15 16 16 17 18
18 19 20 20 20 21 22 22 22 23
24 24 26 26 28 30 32 32 34 34

Before we draw a histogram, let’s consider a couple of questions.

  • What are the smallest and largest values in our data set? This gives us an idea of the distance on the number line that our histogram will cover. In this case, the minimum is 10 and the maximum is 34, so our number line needs to extend from 10 to 35 at the very least.

    (Remember the convention we use to mark off the number line for a histogram: we include the left boundary of a bar but exclude the right boundary. If 34 is the right boundary of the last bar, it won't be included in that bar, so the number line needs to go a little greater than the maximum value.)

  • What group size or bin size seems reasonable here? We could organize the weights into bins of 2 kilograms (10, 12, 14, . . .), 5 kilograms, (10, 15, 20, 25, . . .), 10 kilograms (10, 20, 30, . . .), or any other size. The smaller the bins, the more bars we will have, and vice versa.  

Let’s use bins of 5 kilograms for the dog weights. The boundaries of our bins will be: 10, 15, 20, 25, 30, 35. We stop at 35 because it is greater than the maximum.

Next, we find the frequency for the values in each group. It is helpful to organize the values in a table.

  weights in kilograms frequency
row 1 10 to less than 15 5
row 2 15 to less than 20 7
row 3 20 to less than 25 10
row 4 25 to less than 30 3
row 5 30 to less than 35 5

Now we can draw the histogram.

A histogram: The horizontal axis is labeled “dog weights in kilograms” and the numbers 10 through 35, in increments of 5, are indicated. On the vertical axis the numbers 0 through 10, in increments of 2, are indicated. The data represented by the bars are as follows: Weight from 10 up to 15, 5. Weight from 15 up to 20, 7. Weight from 20 up to 25, 10. Weight from 25 up to 30, 3. Weight from 30 up to 35, 5.

The histogram allows us to learn more about the dog weight distribution and describe its center and spread.

Practice Problems ▶