Lesson 12: Fractional Lengths

Let’s solve problems about fractional lengths.

12.1: Number Talk: Multiplication Strategies

Find the product mentally.

19\boldcdot 14

12.2: How Many Would It Take? (Part 1)

  1. Jada was using square stickers with a side length of \frac 34 inch to decorate the spine of a photo album. The spine is 10\frac12 inches long. If she laid the stickers side by side without gaps or overlaps, how many stickers did she use to cover the length of the spine?
  2. How many \frac58-inch binder clips, laid side by side, make a length of 11\frac14 inches?

  3. It takes exactly 26 paper clips laid end to end to make a length of 17\frac78 inches.

    1. Estimate the length of each paper clip.

    2. Calculate the length of each paper clip. Show your reasoning.

12.3: How Many Times as Tall or as Far?

  1. A second-grade student is 4 feet tall. Her teacher is 5\frac23 feet tall.
    1. How many times as tall as the student is the teacher?
    1. What fraction of the teacher’s height is the student’s height?
  2. Find each quotient. Show your reasoning and check your answer.
    1. 9 \div \frac35
    1. 1\frac78 \div \frac 34

  3. Write a division expression that can help answer each of the following questions. Then answer the question. If you get stuck, draw a diagram.

    1. A runner ran 1\frac45 miles on Monday and 6\frac{3}{10} miles on Tuesday. How many times her Monday’s distance was her Tuesday’s distance?
    2. A cyclist planned to ride 9\frac12 miles but only managed to travel 3\frac78 miles. What fraction of his planned trip did he travel?

12.4: Comparing Paper Rolls

The photo shows a situation that involves fractions.

  1. Use the photo to help you complete the following statements. Explain or show your reasoning for the second statement.

    1. The length of the long paper roll is about ______ times the length of the short paper roll.

    2. The length of the short paper roll is about ______ times the length of the long paper roll.

  2. If the length of the long paper roll is 11 \frac 14 inches, what is the length of each short paper roll?

    Use the information you have about the paper rolls to write a multiplication equation or a division equation for the question. Note that 11 \frac 14 = \frac{45}{4}.

  3. Answer the question. If you get stuck, draw a diagram.

Summary

Division can help us solve comparison problems in which we find out how many times as large or as small one number is compared to another. Here is an example. 

A student is playing two songs for a music recital. The first song is 1\frac12 minutes long. The second song is 3 \frac34 minutes long.

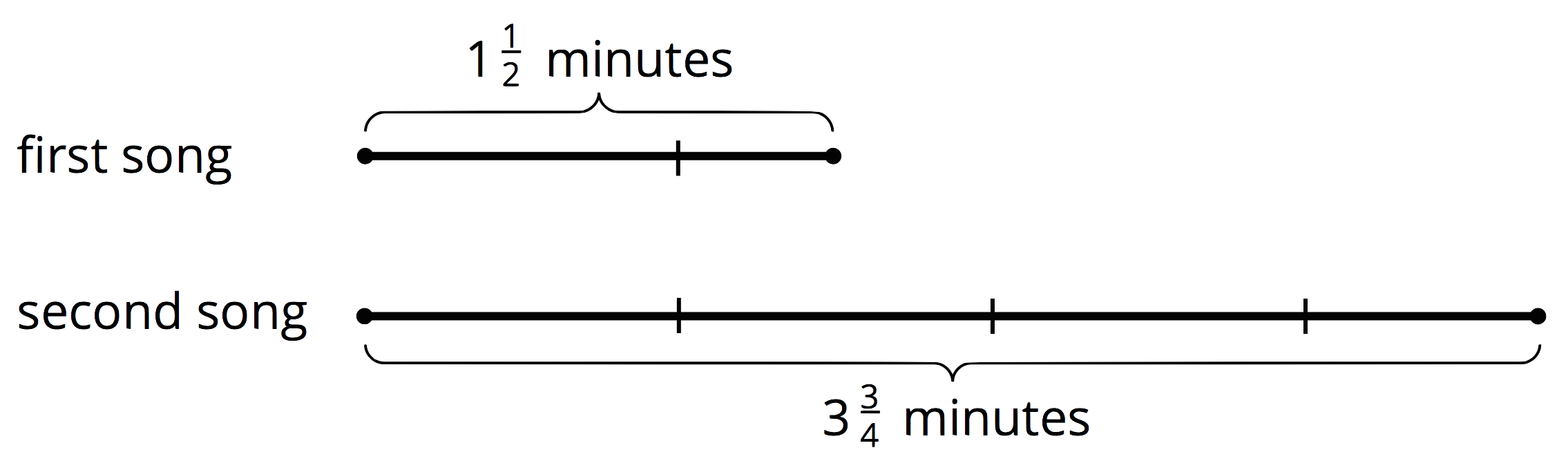
We can ask two different comparison questions and write different multiplication and division equations to represent each question. 
  • How many times as long as the first song is the second song? 

{?} \boldcdot 1\frac12 = 3\frac 34 3 \frac 34 \div 1\frac 12 = {?}

Let’s use the algorithm we learned to calculate the quotient:\begin {align} &3 \frac 34 \div 1\frac 12\\[10px] &= \frac {15}{4} \div \frac 32\\[10px] &= \frac {15}{4} \boldcdot \frac 23\\[10px] &=\frac {30}{12}\\[10px]&=\frac {5}{2}\\[10px] \end {align}

This means the second song is 2\frac 12 times as long as the first song.

  • What fraction of the second song is the first song?

{?} \boldcdot 3\frac 34 = 1\frac 12 1\frac12 \div 3\frac34 = {?}

Let’s calculate the quotient:

\begin {align} &1\frac 12\div 3 \frac 34\\[10px] &=\frac 32 \div \frac {15}{4}\\[10px] &=\frac 32 \boldcdot \frac {4}{15}\\[10px] &=\frac {12}{30}\\[10px] &=\frac {2}{5} \end {align}

The first song is \frac 25 as long as the second song.

Practice Problems ▶