Lesson 12: Navigating a Table of Equivalent Ratios

Let’s use a table of equivalent ratios like a pro.

12.1: Number Talk: Multiplying by a Unit Fraction

Find the product mentally.

$\frac13\boldcdot 21$

$\frac16 \boldcdot 21$

$(5.6) \boldcdot \frac18$

$\frac14\boldcdot (5.6)$

12.2: Comparing Taco Prices

  number of tacos price in dollars
row 1    
row 2    
row 3    
row 4    
row 5    

Use the table to help you solve these problems. Explain or show your reasoning.

  1. Noah bought 4 tacos and paid \$6. At this rate, how many tacos could he buy for \$15?
  2. Jada’s family bought 50 tacos for a party and paid \$72. Were Jada’s tacos the same price as Noah’s tacos?

12.3: Hourly Wages

Lin is paid \$90 for 5 hours of work. She used the following table to calculate how much she would be paid at this rate for 8 hours of work.

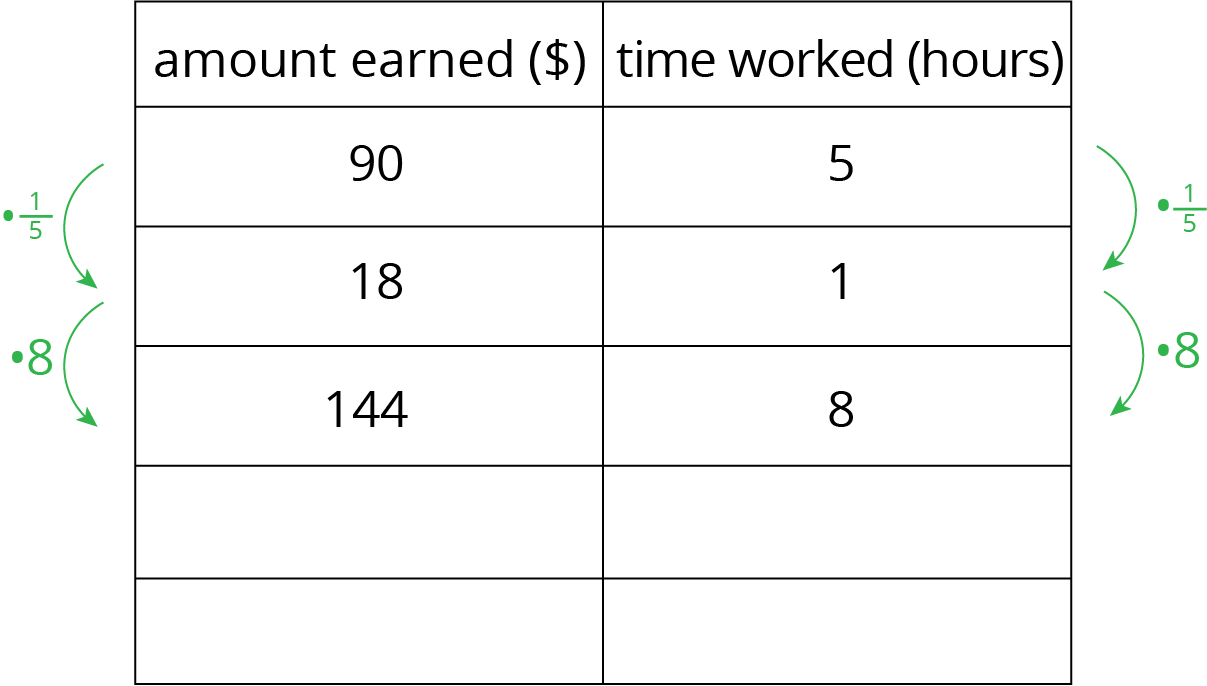
A 2-column table with 5 rows of data. The first column is labeled "amount earned, in dollars" and the second column is labeled "time worked, in hours." Row 1: 90, 5; Row 2: 18, 1; Row 3: 144, 8; Row 4: blank, 3; Row 5: blank, 2.1. An arrow pointing from row 1 to row 2 is labeled "times one-fifth" and another arrow pointing from row 2 to row 3 is labeled "times 8."
  1. What is the meaning of the 18 that appears in the table?
  2. Why was the number $\frac15$ used as a multiplier?
  1. Explain how Lin used this table to solve the problem.

  2. At this rate, how much would Lin be paid for 3 hours of work? For 2.1 hours of work?

12.4: Zeno’s Memory Card

In 2016, 128 gigabytes (GB) of portable computer memory cost \$32.

  1. Here is a double number line that represents the situation:

    A double number line: For "memory, in gigabytes" the numbers 0, 64, and 128 are indicated. For "cost, in dollars" the numbers 0, 16, and 32 are indicated.
     

    One set of tick marks has already been drawn to show the result of multiplying 128 and 32 each by $\frac12$. Label the amount of memory and the cost for these tick marks.

    Next, keep multiplying by $\frac12$ and drawing and labeling new tick marks, until you can no longer clearly label each new tick mark with a number.

  2. Here is a table that represents the situation. Find the cost of 1 gigabyte. You can use as many rows as you need.

  memory (gigabytes) cost (dollars)
row 1 128 32
row 2    
row 3    
row 4    
row 5    
row 6    
row 7    
row 8    
  1. Did you prefer the double number line or the table for solving this problem? Why?

Summary

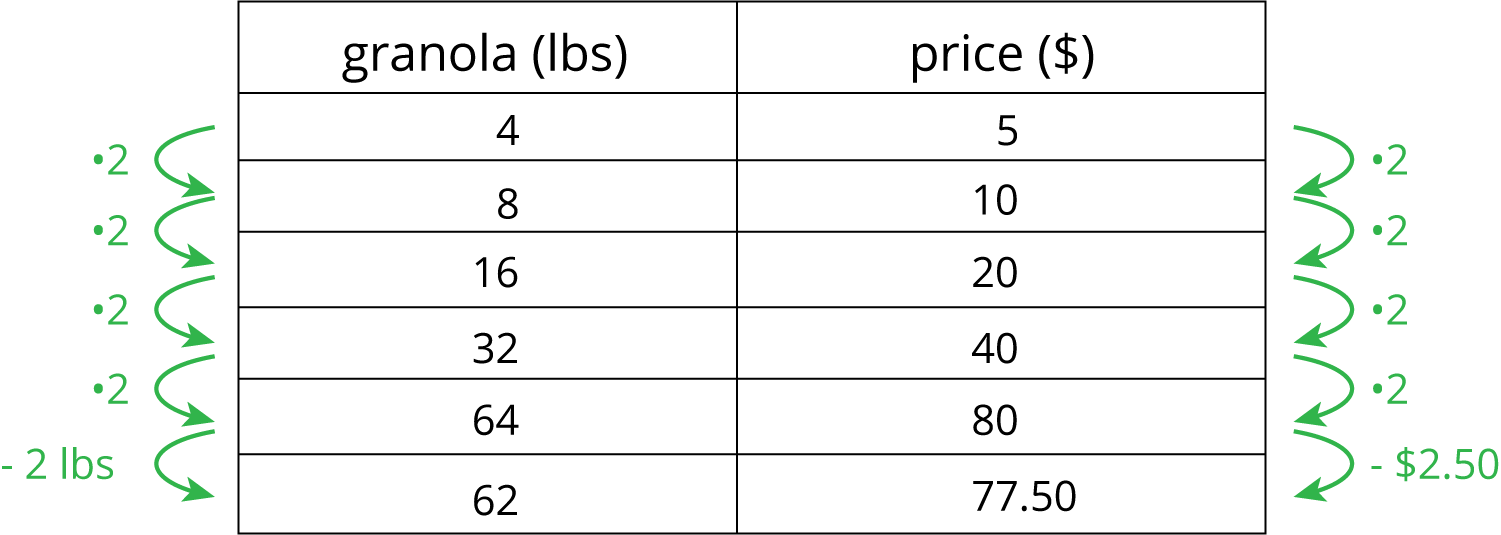
Finding a row containing a “1” is often a good way to work with tables of equivalent ratios. For example, the price for 4 lbs of granola is \$5. At that rate, what would be the price for 62 lbs of granola?

Here are tables showing two different approaches to solving this problem. Both of these approaches are correct. However, one approach is more efficient.

  • Less efficient

    A 2-column table with 6 rows of data. The first column is labeled "granola, in pounds" and the second column is labeled "price, in dollars." Row 1: 4, 5; Row 2: 8, 10; Row 3: 16, 20; Row 4: 32, 40; Row 5: 64, 80; Row 6: 62, 77.50. An arrow pointing from row 1 to row 2, then 2 to 3, then 3 to 4, then 4 to 5 is labeled "times 2". The last arrow from row 5 to 6 is labeled "subtract 2 pounds" on the left of the table and is labeled " subtract "$2.50" on the right.

  • More efficient

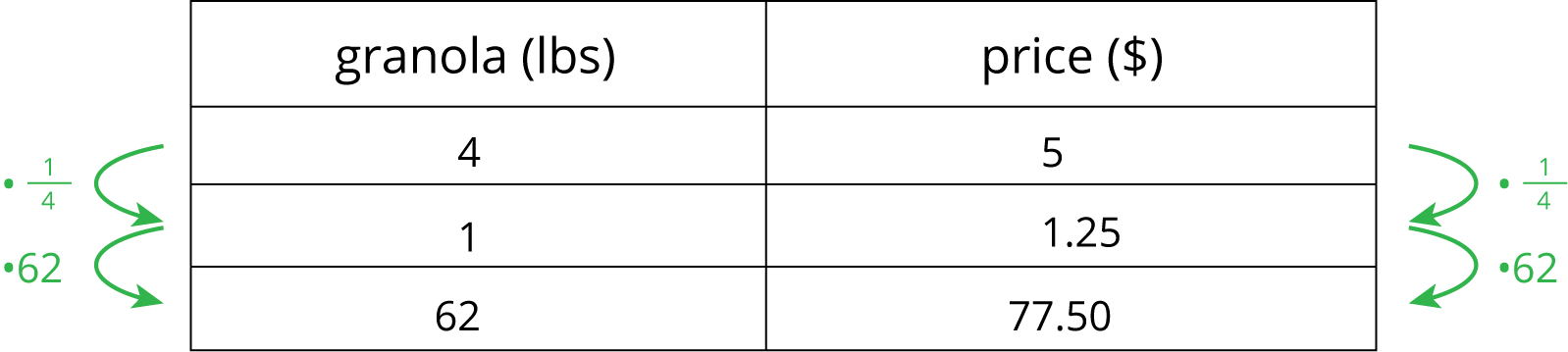
    A 2-column table with 3 rows of data. The first column is labeled "granola, in pounds" and the second column is labeled " price, in dollars." Row 1: 4, 5; Row 2: 1, 1.25; Row 3: 62, 77.50. An arrow pointing from row 1 to row 2 is labeled "times one-fourth" and another arrow pointing from row 2 to row 3 is labeled "times 62."

Notice how the more efficient approach starts by finding the price for 1 lb of granola.

Remember that dividing by a whole number is the same as multiplying by a unit fraction. In this example, we can divide by 4 or multiply by $\frac14$ to find the unit price.

Practice Problems ▶