Let’s look at division problems that help us find the size of one group.
To make 5 batches of cookies, 10 cups of flour are required. How many cups of flour does each batch require?
We can write equations and draw a diagram to represent this situation. They help us see that each batch requires 2 cups of flour.
$$5\, \boldcdot {?} = 10$$ $$10 \div 5 = {?}$$
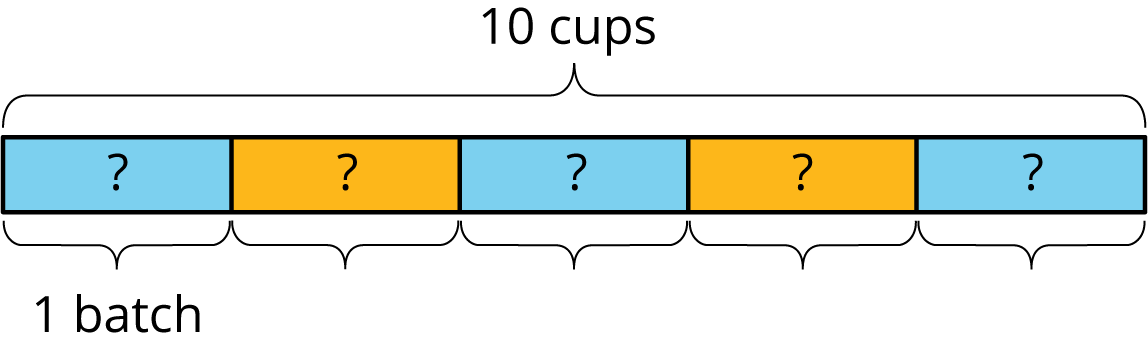
For each question, write a multiplication equation and a division equation, draw a diagram, and answer the question.
Here are three tape diagrams and three descriptions of situations that include questions.
Match a diagram to each situation, then use the diagram to help you answer the question. Next, write multiplication and division equations to represent each situation.
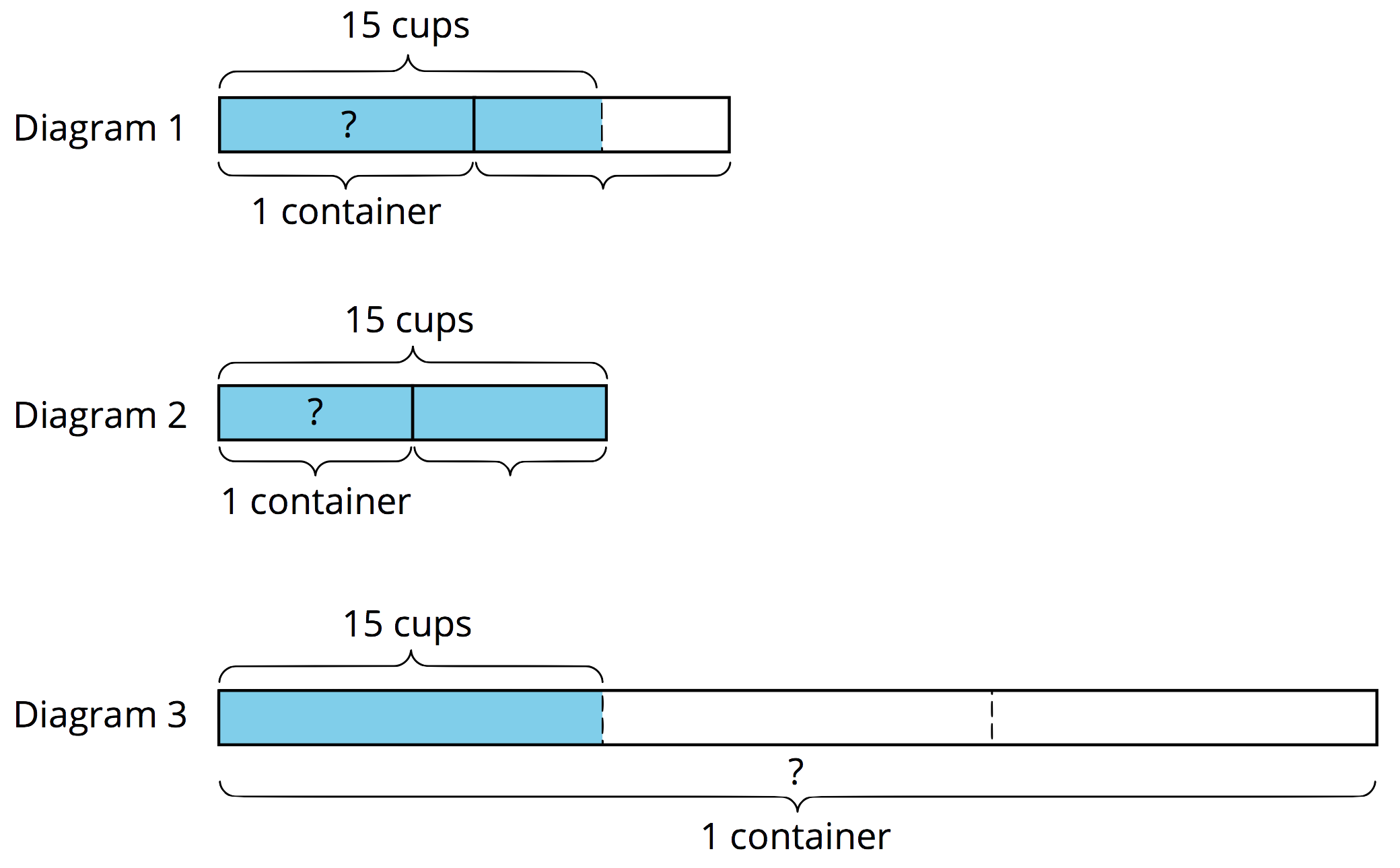
Tyler poured 15 cups of water into 2 equal-sized bottles and filled each bottle. How much water was in each bottle?
Diagram:
Answer:
Multiplication equation:
Division equation:
Kiran poured 15 cups of water into equal-sized pitchers and filled $1\frac12$ pitchers. How much water was in the full pitcher?
Diagram:
Answer:
Multiplication equation:
Division equation:
It takes 15 cups of water to fill $\frac13$ pail. How much water is needed to fill 1 pail?
Diagram:
Answer:
Multiplication equation:
Division equation:
Here are three more diagrams and situations. Match a diagram to each situation, and use the diagram to help you answer the question. Next, write multiplication and division equations to represent each situation.
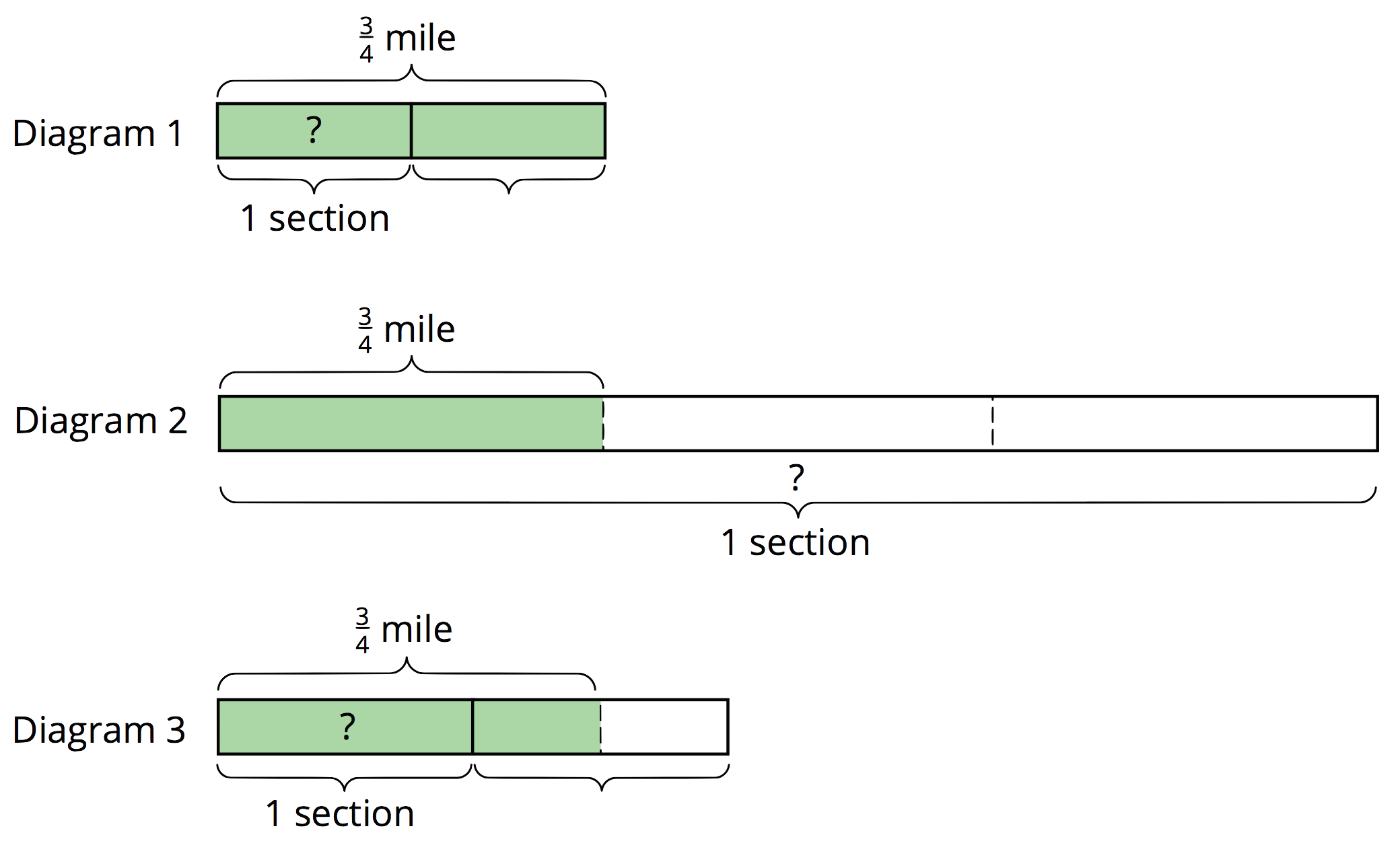
Priya’s class has adopted two equal sections of a highway to keep clean. The combined length is $\frac34$ of a mile. How long is each section?
Diagram:
Answer:
Multiplication equation:
Division equation:
Lin’s class has also adopted some sections of highway to keep clean. If $1\frac12$ sections are $\frac34$ mile long, how long is each section?
Diagram:
Answer:
Multiplication equation:
Division equation:
A school has adopted a section of highway to keep clean. If $\frac13$ of the section is $\frac34$ mile long, how long is the section?
Diagram:
Answer:
Multiplication equation:
Division equation:
To make a Cantor ternary set:
Sometimes we know the amount for multiple groups, but we don’t know how much is in one group. We can use division to find out.
For example: If 5 people share $ 8 \frac12$ pounds of cherries equally, how many pounds of cherries does each person get?
We can represent this situation as a multiplication and a division: $$5\, \boldcdot {?} = 8\frac12$$ $$8 \frac12 \div 5 = {?}$$
$8\frac12 \div 5$ can be written as $\frac{17}{2} \div 5$. Dividing by 5 is equivalent to multiplying by $\frac 15$, and $\frac{17}{2} \boldcdot \frac {1}{5} =\frac {17}{10}$. This means each person gets $1\frac {7}{10}$ pounds.
Other times, we know the amount for a fraction of a group, but we don’t know the size of one whole group. We can also use division to find out.
For example: Jada poured 5 cups of iced tea in a pitcher and filled $\frac 23$ of the pitcher. How many cups of iced tea fill the entire pitcher?
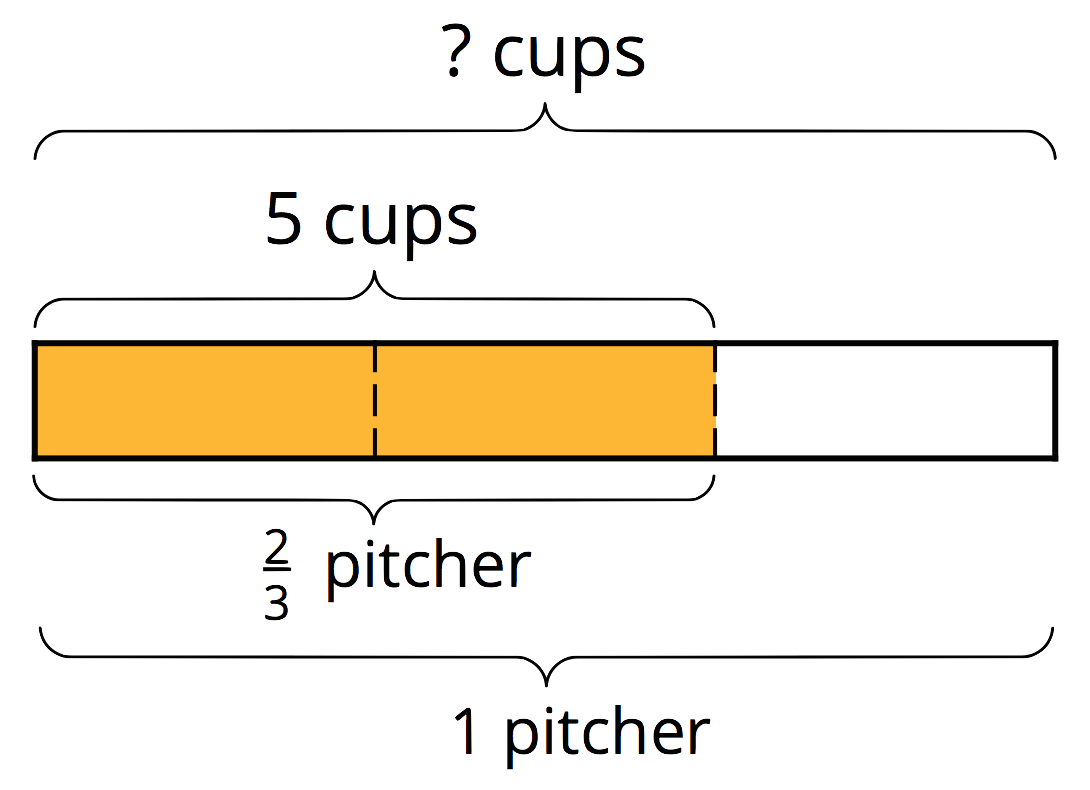
We can represent this situation as a multiplication and a division: $$\frac 23 \boldcdot {?} = 5$$ $$5 \div \frac23 = {?}$$
The diagram can help us reason about the answer. If $\frac23$ of a pitcher is 5 cups, then $\frac 13$ of a pitcher is half of 5, which is $\frac52$. Because there are 3 thirds in 1 whole, there would be $(3 \boldcdot \frac52)$ or $\frac{15}{2}$ cups in one whole pitcher. We can check our answer by multiplying: $\frac23 \boldcdot \frac {15}{2} = \frac {30}{6}$, and $\frac {30}{6} = 5$.
Notice that in the first example, the number of groups is greater than 1 (5 people) and in the second, the number of groups is less than 1 ($\frac 23$ of a pitcher), but the division and multiplication equations for both have the same structures.
