Let's investigate what dot plots and bar graphs can tell us.
Fifteen customers in a pizza shop were asked, “How many toppings did you add to your cheese pizza?” Their responses are shown in the table.
| 1 | 2 | 1 | 3 | 0 | 1 | 1 | 2 | 0 | 3 | 0 | 0 | 1 | 2 | 2 |
Complete the table.
| number of toppings | frequency (number) | |
|---|---|---|
| row 1 | 0 | |
| row 2 | 1 | |
| row 3 | 2 | |
| row 4 | 3 |
Use the tables from the warm-up to display the number of toppings as a dot plot. Label your drawing clearly.
Think of a statistical question that can be answered with the data about the number of toppings ordered, as displayed on the dot plot. Then answer this question.
Use the dot plot to answer the following questions. For each, show or explain your reasoning.
Someone said, “In general, these students spend roughly the same number of hours doing homework.” Do you agree? Explain your reasoning.
We often collect and analyze data because we are interested in learning what is “typical,” or what is common and can be expected in a group.
Sometimes it is easy to tell what a typical member of the group is. For example, we can say that a typical shape in this set is a large circle.
Just looking at the members of a group doesn’t always tell us what is typical, however. For example, if we are interested in the side length typical of squares in this set, it isn’t easy to do so just by studying the set visually.
In a situation like this, it is helpful to gather the side lengths of the squares in the set and look at their distribution, as shown in this dot plot.
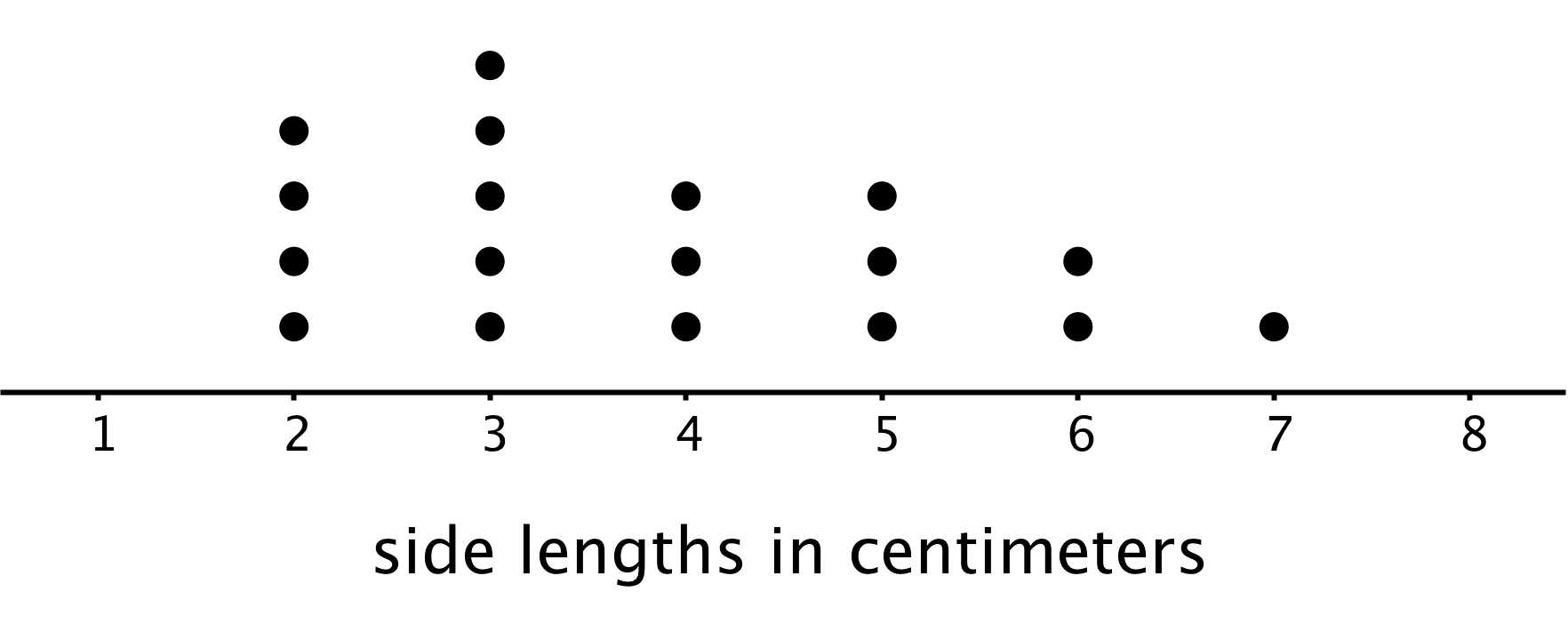
We can see that many of the data points are between 2 and 4, so we could say that side lengths between 2 and 4 centimeters or close to these lengths are typical of squares in this set.
