3.1: Squares in Rectangles
-
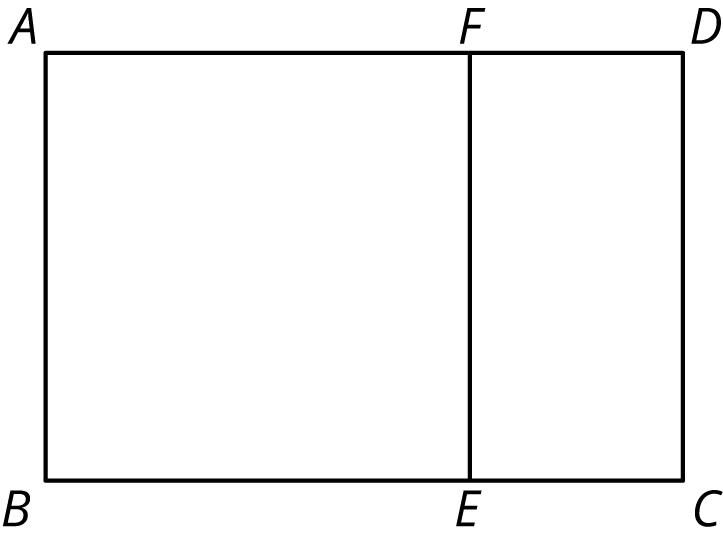
Rectangle ABCD is not a square. Rectangle ABEF is a square.
-
Suppose segment AF were 5 units long and segment FD were 2 units long. How long would segment AD be?
-
Suppose segment BC were 10 units long and segment BE were 6 units long. How long would segment EC be?
-
Suppose segment AF were 12 units long and segment FD were 5 units long. How long would segment FE be?
-
Suppose segment AD were 9 units long and segment AB were 5 units long. How long would segment FD be?
-
-
Rectangle JKXW has been decomposed into squares.
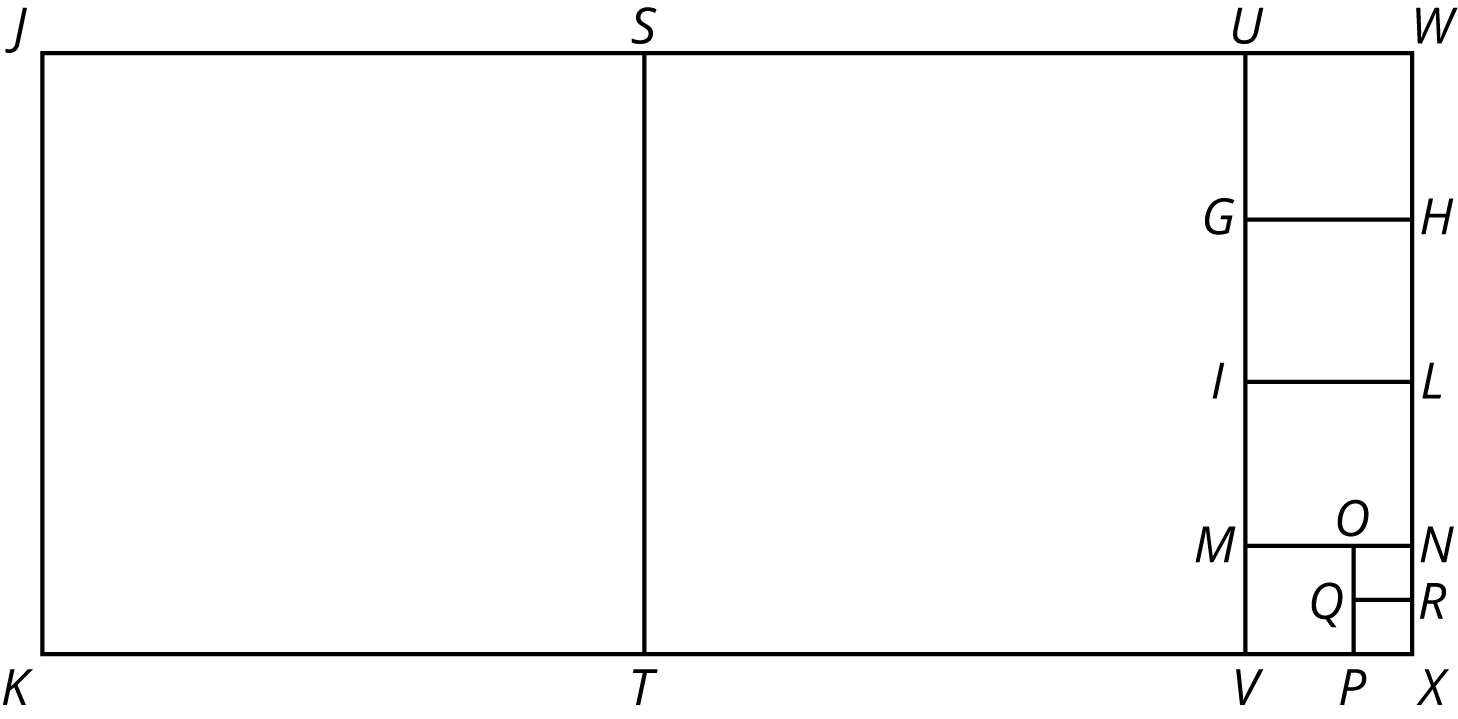
Segment JK is 33 units long and segment JW is 75 units long. Find the areas of all of the squares in the diagram.
-
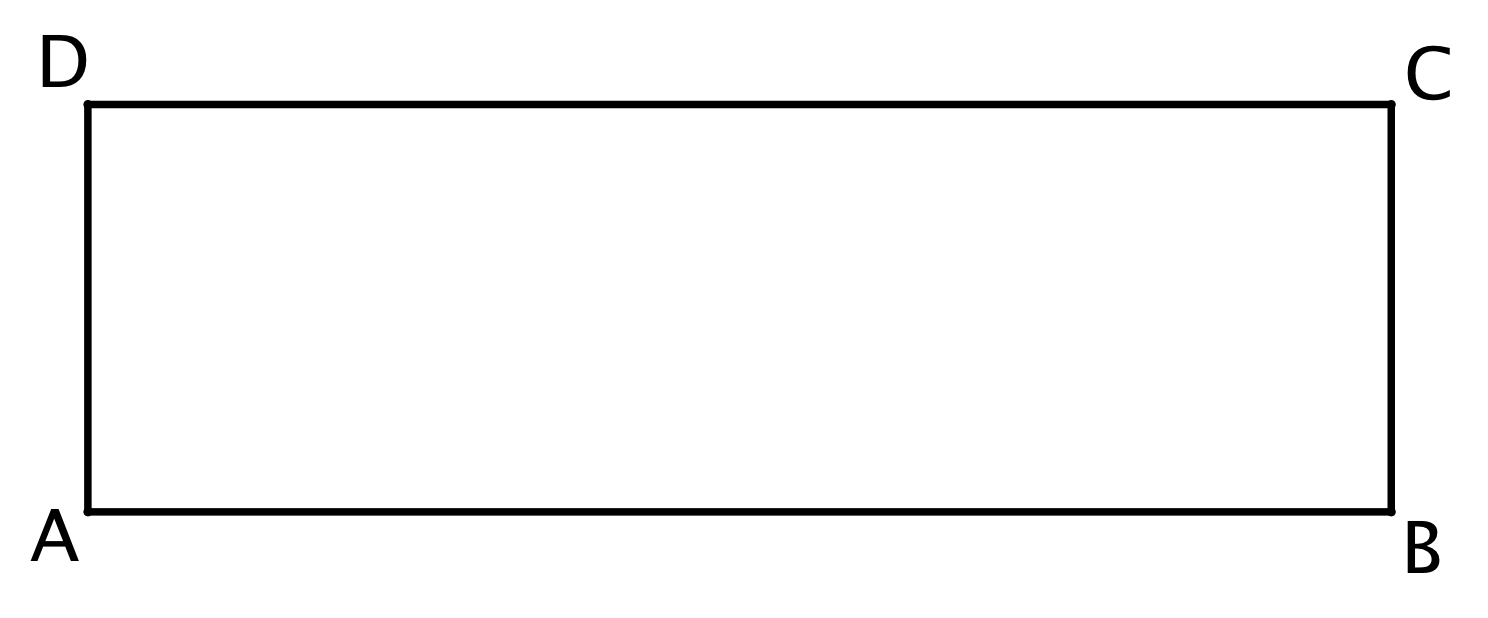
Rectangle ABCD is 16 units by 5 units.
-
In the diagram, draw a line segment that decomposes ABCD into two regions: a square that is the largest possible and a new rectangle.
-
Draw another line segment that decomposes the new rectangle into two regions: a square that is the largest possible and another new rectangle.
-
Keep going until rectangle ABCD is entirely decomposed into squares.
- List the side lengths of all the squares in your diagram.
-
-
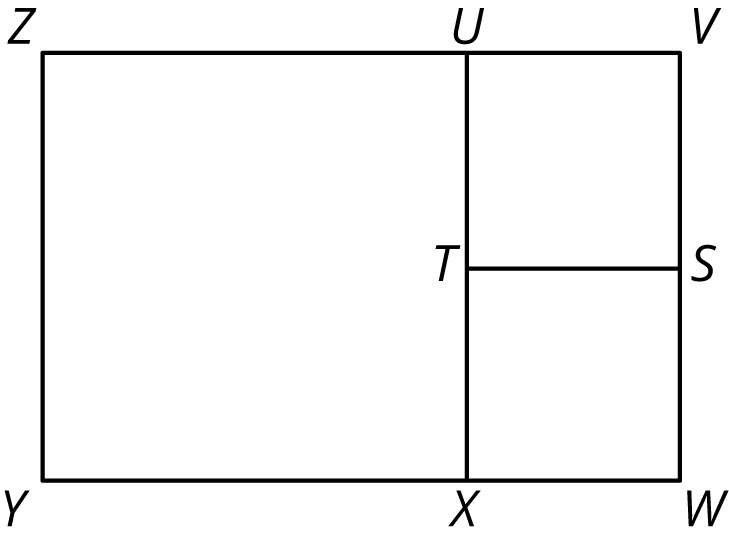
The diagram shows that rectangle VWYZ has been decomposed into three squares. What could the side lengths of this rectangle be?
-
How many different side lengths can you find for rectangle VWYZ?
-
What are some rules for possible side lengths of rectangle VWYZ?