Lesson 12: What is Surface Area?

Let’s cover the surfaces of some three-dimensional objects.

12.1: Covering the Cabinet (Part 1)

Your teacher will show you a video about a cabinet or some pictures of it.

Estimate an answer to the question: How many sticky notes would it take to cover the cabinet, excluding the bottom?

12.2: Covering the Cabinet (Part 2)

Earlier, you learned about a cabinet being covered with sticky notes.

  1. How could you find the actual number of sticky notes it will take to cover the cabinet, excluding the bottom? What information would you need to know?
  2. Use the information you have to find the number of sticky notes to cover the cabinet. Show your reasoning.

12.3: Building with Snap Cubes

Here is a rectangular prism built from 12 cubes:

It has six faces, but you can only see three of them in the sketch. It has a surface area of 32 square units.

The applet has 12 blocks, too. They are all in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. To use a block, drag the red point to move it. Click on the red points to change from left/right movement to up/down movement.

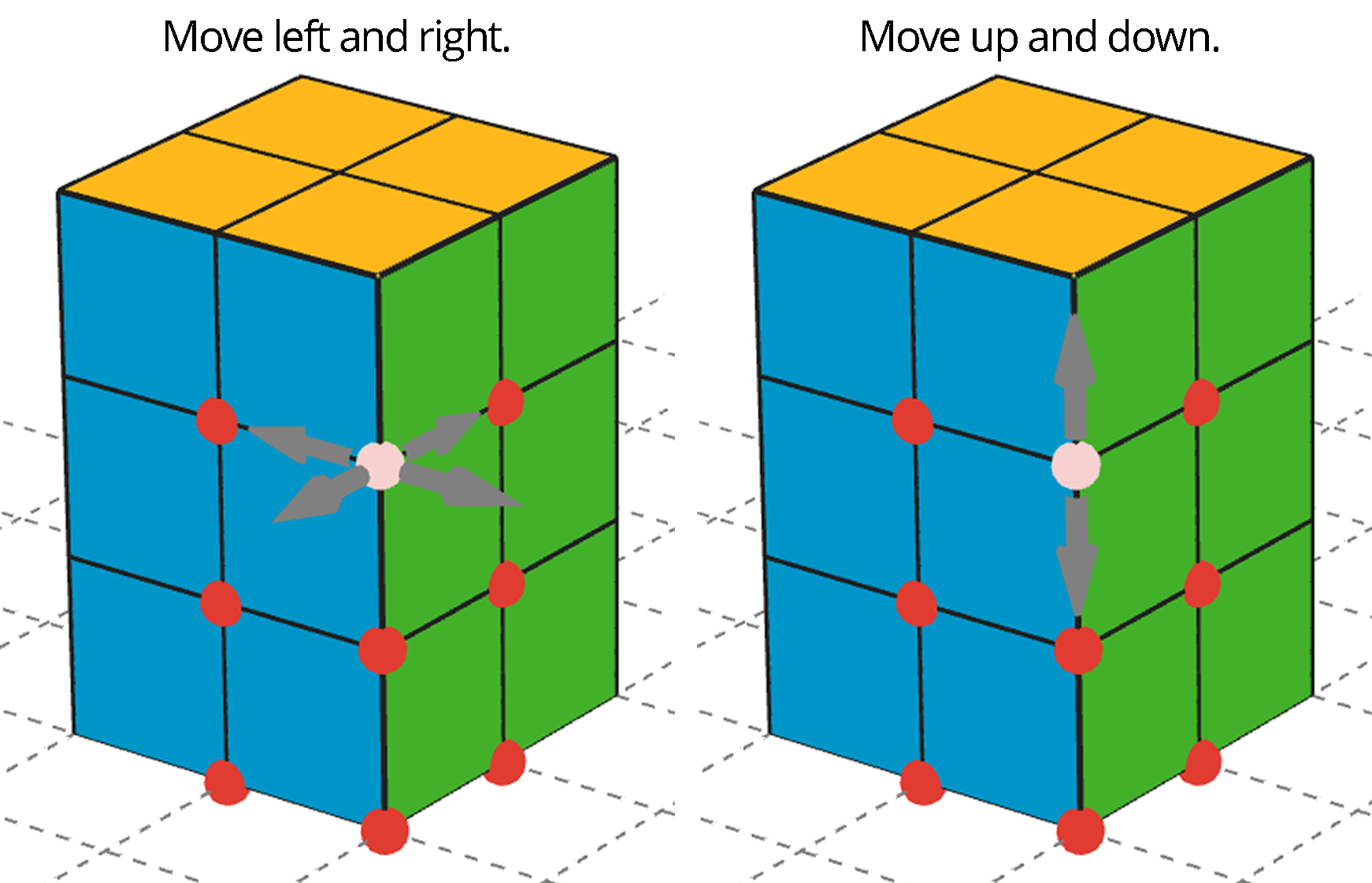
Use all 12 cubes to build a different rectangular prism (with different edge lengths than shown in the prism here). You can turn the view to see all of the faces of your figure.

GeoGebra Applet pxu4G7CK

  1. How many faces does your figure have?
  2. What is the surface area of your figure in square units?

Summary

  • The surface area of a figure (in square units) is the number of unit squares it takes to cover the entire surface without gaps or overlaps.
  • If a three-dimensional figure has flat sides, the sides are called faces.
  • The surface area is the total of the areas of the faces.

For example, a rectangular prism has six faces. The surface area of the prism is the total of the areas of the six rectangular faces.

“”

So the surface area of a rectangular prism that has edge-lengths 2 cm, 3 cm, and 4 cm has a surface area of $$(2\boldcdot 3)+ (2\boldcdot 3) + (2\boldcdot 4) + (2\boldcdot 4) + (3\boldcdot 4) + (3\boldcdot 4)$$ or 52 square centimeters.

Practice Problems ▶

Glossary

surface area

surface area

The surface area (in square units) is the number of unit squares it takes to cover all the surfaces of a three-dimensional figure without gaps or overlaps.

face

face

Any flat surface on a three-dimensional figure is a face.