Lesson 12: Dividing Decimals by Whole Numbers

Let’s divide decimals by whole numbers.

12.1: Number Talk: Dividing by 4

Find each quotient mentally.

$80 \div 4$

$12 \div 4$

$1.2 \div 4$

$81.2 \div 4$

12.2: Using Diagrams to Represent Division

To find $53.8 \div 4$ using diagrams, Elena began by representing 53.8. 

She placed 1 ten into each group, unbundled the remaining 1 ten into 10 ones, and went on distributing the units.

This diagram shows Elena’s initial placement of the units and the unbundling of 1 ten.

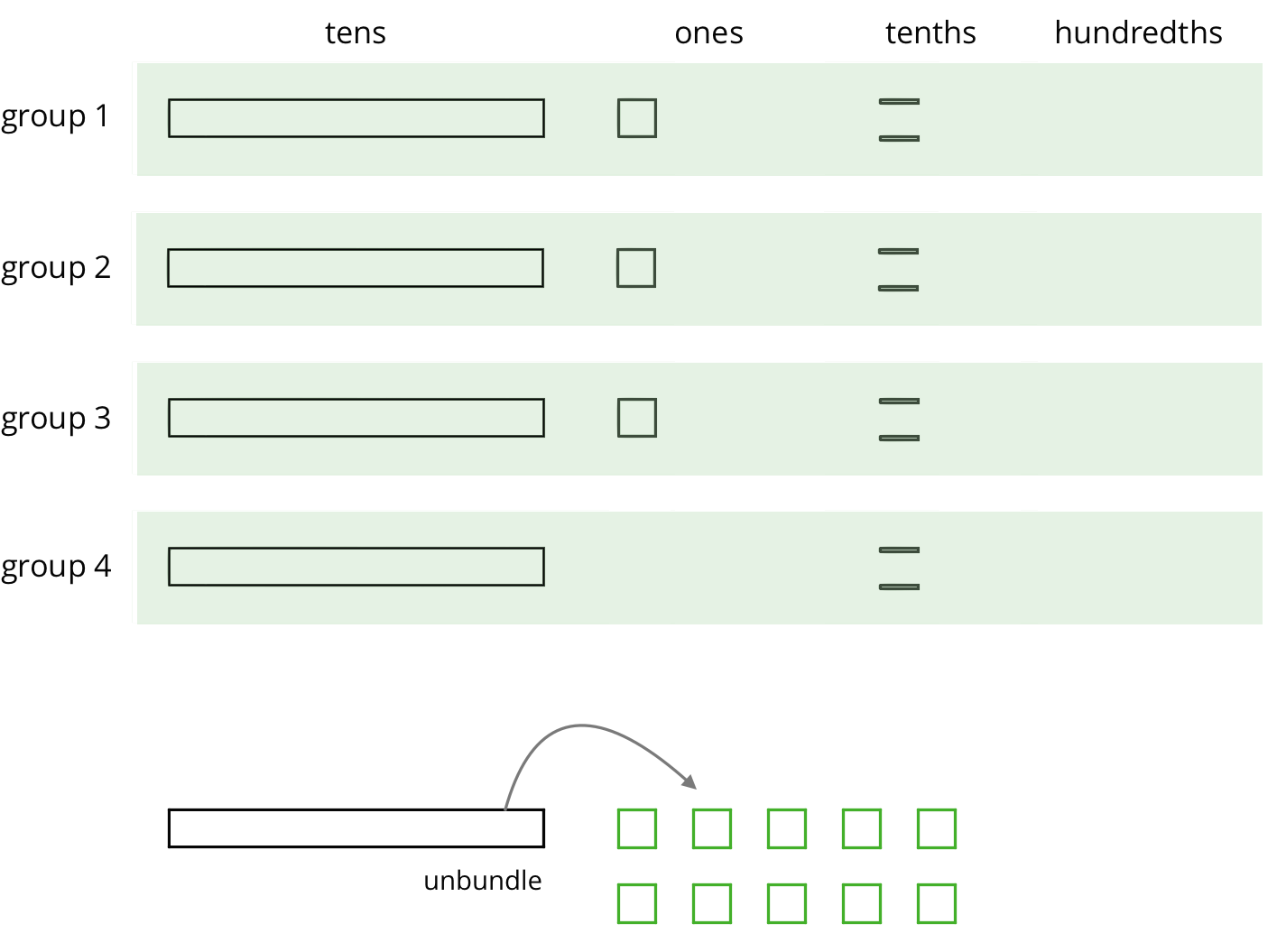
  1. Complete the diagram by continuing the division process. How would you use the available units to make 4 equal groups?

    As the units get placed into groups, show them accordingly and cross out those pieces from the bottom. If you unbundle a unit, draw the resulting pieces. 

  2. What value did you find for $53.8 \div 4$? Be prepared to explain your reasoning.

  1. Use long division to find $53.8 \div 4$. Check your answer by multiplying it by the divisor 4.
  1. Use long division to find $77.4 \div 5$. If you get stuck, you can draw diagrams or use another method.

12.3: Dividends and Divisors

Analyze the dividends, divisors, and quotients in the calculations, then answer the questions.

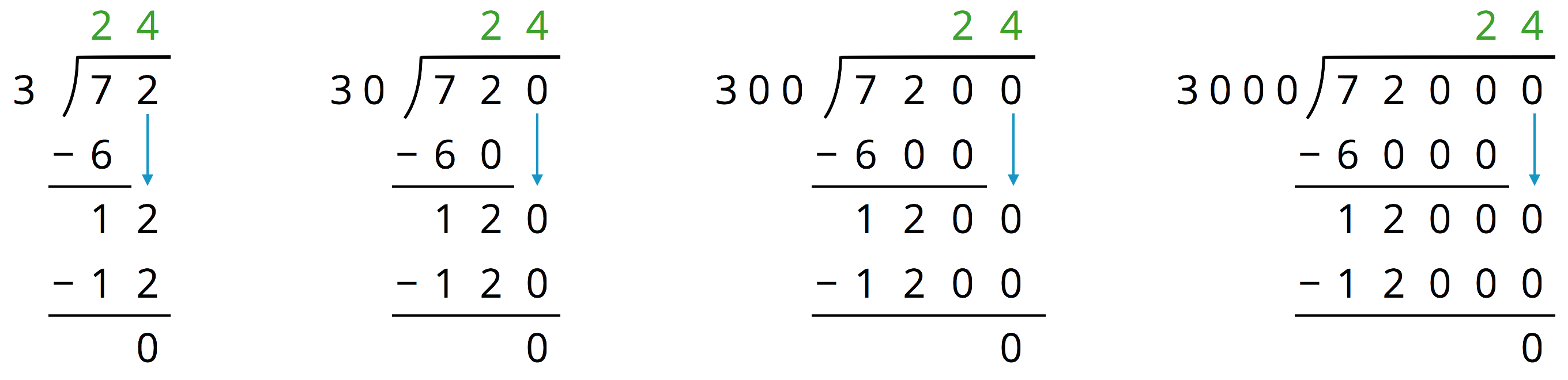
  1. Complete each sentence. In the calculations above:

    • Each dividend is ______ times the dividend to the left of it.

    • Each divisor is ______ times the divisor to the left of it. 

    • Each quotient is _____________________ the quotient to the left of it.

  2. Suppose we are writing a calculation to the right of $72,\!000 \div 3,\!000$. Which expression has a quotient of 24? Be prepared to explain your reasoning.

    1. $72,\!000 \div 30,\!000$
    2. $720,\!000 \div 300,\!000$
    1. $720,\!000 \div 30,\!000$
    2. $720,\!000 \div 3,\!000$
  3. Suppose we are writing a calculation to the left of $72 \div 3$. Write an expression that would also give a quotient of 24. Be prepared to explain your reasoning.

  4. Decide which of the following expressions would have the same value as $250 \div 10$. Be prepared to share your reasoning.

    1. $250 \div 0.1$
    2. $25 \div 1$
    1. $2.5 \div 1$
    2. $2.5 \div 0.1$
    1. $2,500 \div 100$
    2. $0.25 \div 0.01$

Summary

We know that fractions such as $\frac 64$ and $\frac {60}{40}$ are equivalent because:

  • Both the numerator and denominator of $\frac {60}{40}$ have a factor of 10, so it can be written as $\frac 64$.
  • Both fractions can be simplified to $\frac 32$.
  • 600 divided by 400 is 1.5, and 60 divided by 40 is also 1.5.

Just like fractions, division expressions can be equivalent. For example, the expressions $540 \div 90$ and $5,\!400 \div 900$ are both equivalent to $54 \div 9$ because:

  • They all have a quotient of 6.
  • The dividend and the divisor in $540 \div 90$ are each 10 times the dividend and divisor in $54 \div 9$. Those in $5,\!400 \div 900$ are each 100 times the dividend and divisor in $54 \div 90$. In both cases, the quotient does not change.

This means that an expression such as $5.4 \div 0.9$ also has the same value as $54 \div 9$. Both the dividend and divisor of $5.4 \div 0.9$ are $\frac {1}{10}$ of those in $54 \div 9$.

In general, multiplying a dividend and a divisor by the same number does not change the quotient. Multiplying by powers of 10 (e.g., 10, 100, 1,000, etc.) can be particularly useful for dividing decimals, as we will see in an upcoming lesson.

Practice Problems ▶