- Estimate the total cost.
- What is the exact cost?
Unit 5: Practice Problem Sets
Lesson 1
Problem 1
Mai had $14.50. She spent $4.35 at the snack bar and $5.25 at the arcade. What is the exact amount of money Mai has left?
- $9.60
- $10.60
- $4.90
- $5.90
Problem 2
A large cheese pizza costs $7.50. Diego has $40 to spend on pizzas. How many large cheese pizzas can he afford? Explain or show your reasoning.
Problem 3
Tickets to a show cost $5.50 for adults and $4.25 for students. A family is purchasing 2 adult tickets and 3 student tickets.
- If the family pays $25, what is the exact amount of change they should receive?
Problem 4
Chicken costs $3.20 per pound, and beef costs $4.59 per pound. Answer each question and show your reasoning.
- What is the exact cost of 3 pounds of chicken?
- What is the exact cost of 3 pound of beef?
- How much more does 3 pounds of beef cost than 3 pounds of chicken?
Problem 5 (from Unit 4, Lesson 16)
- How many \frac15-liter glasses can Lin fill with a 1 \frac12-liter bottle of water?
- How many 1 \frac12-liter bottles of water does it take to fill a 16-liter jug?
Problem 6 (from Unit 4, Lesson 14)
Use the grid to complete this problem.

Let the side length of each small square on the grid represent \frac{1}{2} unit. Draw two different triangles, each with base 5\frac12 units and area 19\frac14 \text{ units}^2. Why does each of your triangles have area 19\frac14 \text{ units}^2? Explain or show your reasoning.
Problem 7 (from Unit 4, Lesson 10)
Find each quotient.
- \frac56 \div \frac16
- 1\frac16 \div \frac{1}{12}
- \frac{10}{6 }\div \frac{1}{24}
Lesson 2
Problem 1
Use the given key to answer the questions.

- What number does this diagram represent?

- Draw a diagram that represents 0.216.
- Draw a diagram that represents 0.304.
Problem 2
Here are diagrams that represent 0.137 and 0.284.
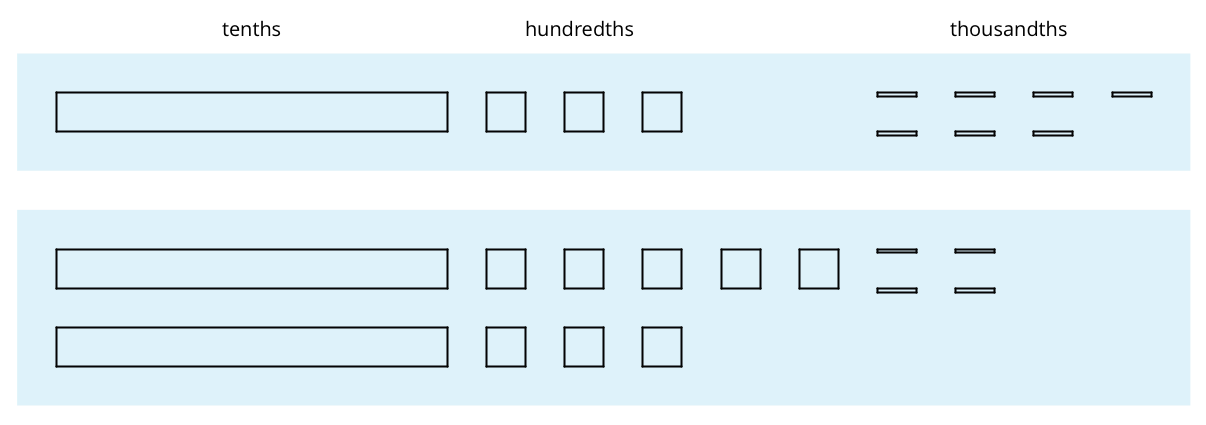
-
Use the diagram to find the value of 0.137 + 0.284. Explain your reasoning.
-
Calculate the sum vertically.
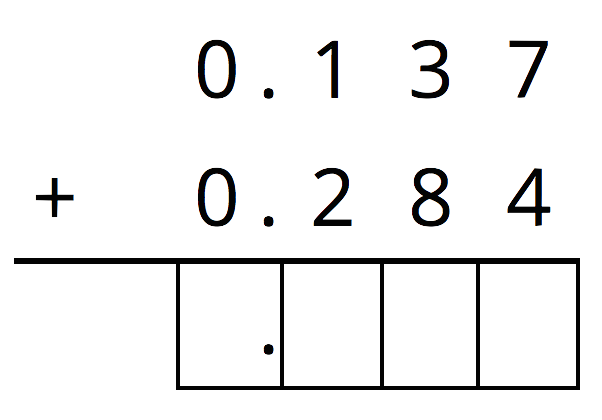
- How was your reasoning in the first two questions different? How was it similar or the same?
Problem 3
For the first two problems, circle the vertical calculation where digits of the same kind are lined up. Then, finish the calculation and find the sum. For the last two problems, find the sum using vertical calculation.
- 3.25+1
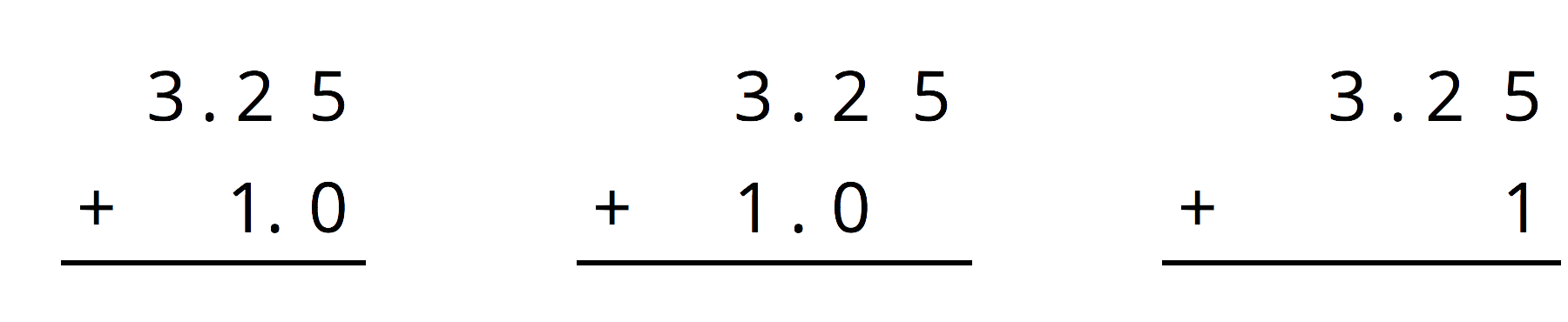
- 0.5+1.15
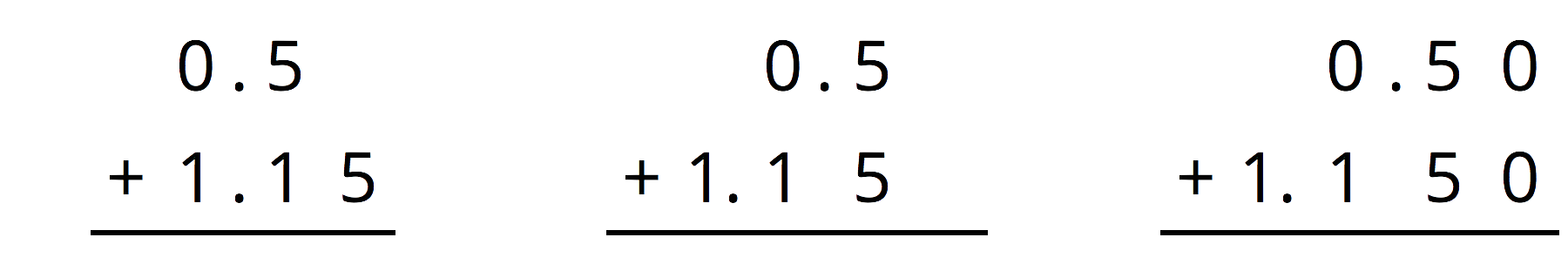
- 10.6+ 1.7
- 123+0.2
Problem 4 (from Unit 2, Lesson 9)
Andre has been practicing his math facts. He can now complete 135 multiplication facts in 90 seconds.
- If Andre is answering questions at a constant rate, how many facts can he answer per second?
- Noah also works at a constant rate, and he can complete 75 facts in 1 minute. Who is working faster? Explain or show your reasoning.
Lesson 3
Problem 1
Here is a base-ten diagram that represents 1.13. Use the diagram to find 1.13 - 0.46.
Explain how you found the difference, or label your diagram to show your steps.
Problem 2
Compute the following sums. If you get stuck, you can draw base-ten diagrams.
-
0.027 + 0.004
-
0.203 + 0.1
-
1.2 + 0.145
Problem 3
A student said we cannot subtract 1.97 from 20 because 1.97 has two decimal digits and 20 has none. Do you agree with his statement? Explain or show your reasoning.
Problem 4
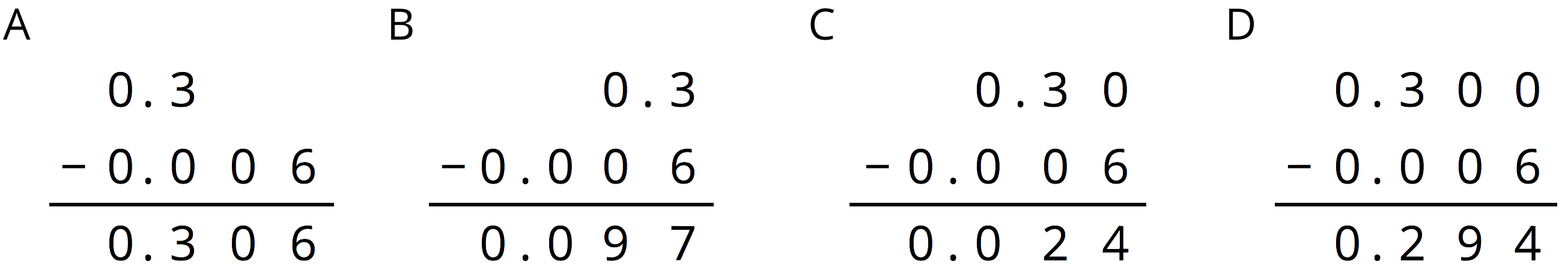
Problem 5
Complete the calculations so that each shows the correct difference.
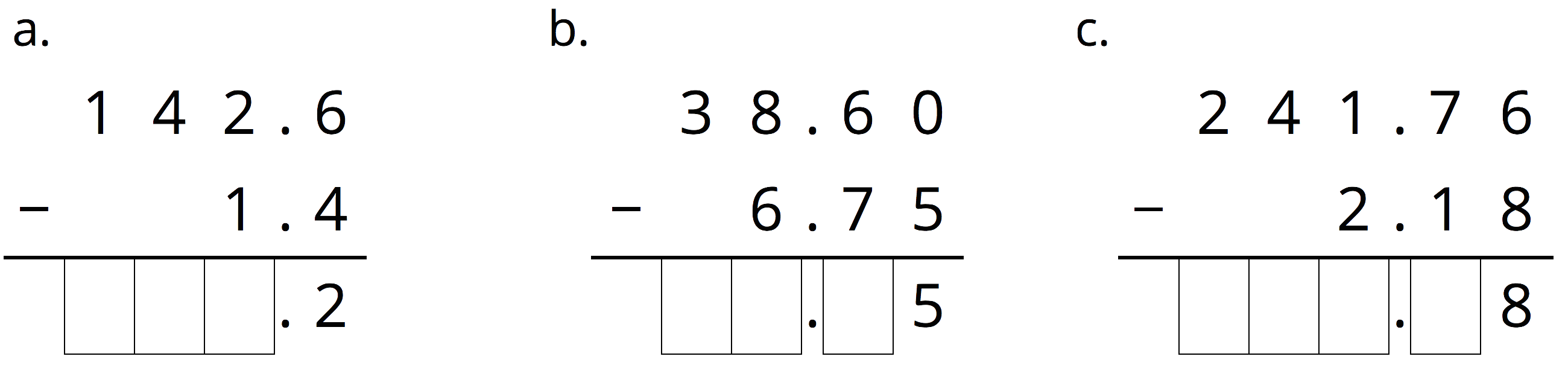
Problem 6 (from Unit 5, Lesson 1)
The school store sells pencils for $0.30 each, hats for $14.50 each, and binders for $3.20 each. Elena would like to buy 3 pencils, a hat, and 2 binders. She estimated that the cost will be less than $20.
- Do you agree with her estimate? Explain your reasoning.
- Estimate the number of pencils could she buy with $5. Explain or show your reasoning.
Problem 7 (from Unit 4, Lesson 15)
A rectangular prism measures 7\frac{1}{2} cm by 12 cm by 15\frac{1}{2} cm.
- Calculate the number of cubes with edge length \frac{1}{2} cm that fit in this prism.
- What is the volume of the prism in \text{cm}^3? Show your reasoning. If you are stuck, think about how many cubes with \frac12-cm edge lengths fit into 1\text{ cm}^3.
Problem 8 (from Unit 2, Lesson 12)
At a constant speed, a car travels 75 miles in 60 minutes. How far does the car travel in 18 minutes? If you get stuck, consider using the table.
| minutes | distance in miles | |
|---|---|---|
| row 1 | 60 | 75 |
| row 2 | 6 | |
| row 3 | 18 |
Lesson 4
Problem 1
For each subtraction problem, circle the correct calculation.
- 7.2 - 3.67
- 16 - 1.4
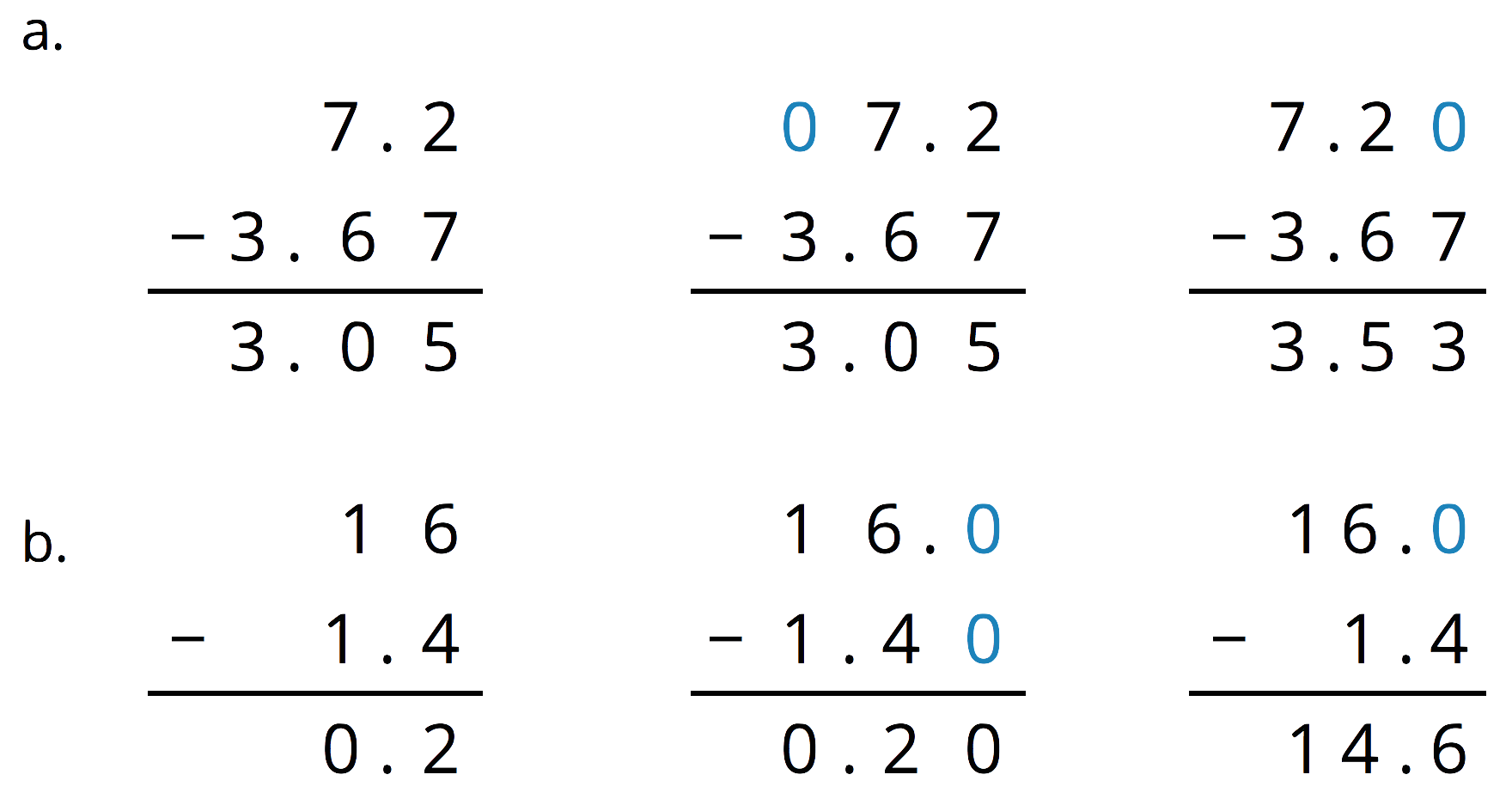
Problem 2
Explain how you could find the difference of 1 and 0.1978.
Problem 3
A bag of chocolates is labeled to contain 0.384 pound of chocolates. The actual weight of the chocolates is 0.3798 pound.
- Are the chocolates heavier or lighter than the weight stated on the label? Explain how you know.
- How much heavier or lighter are the chocolates than stated on the label? Show your reasoning.
Problem 4
Complete the calculations so that each shows the correct sum.
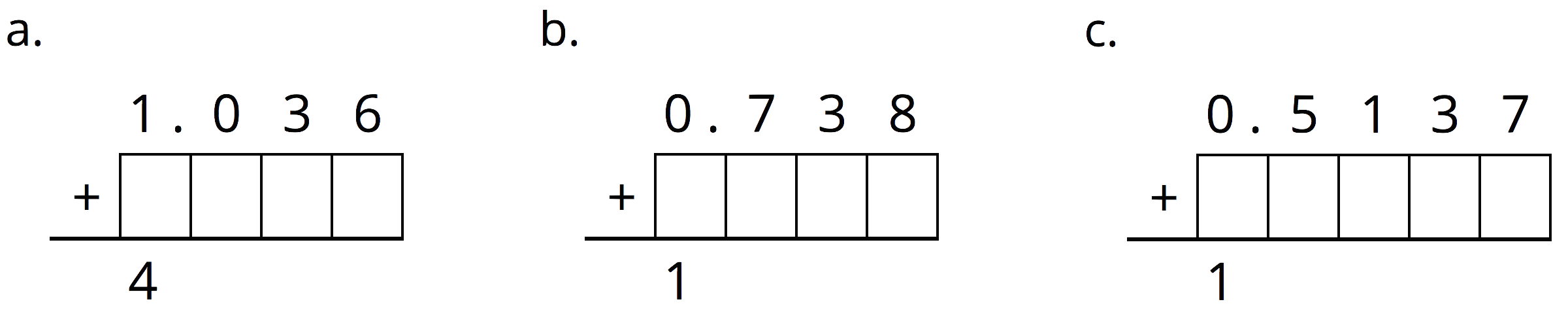
Problem 5 (from Unit 4, Lesson 14)
A shipping company is loading cube-shaped crates into a larger cube-shaped container. The smaller cubes have side lengths of 2\frac12 feet, and the larger shipping container has side lengths of 10 feet. How many crates will fit in the large shipping container? Explain your reasoning.
Problem 6 (from Unit 2, Lesson 13)
For every 9 customers, the chef prepares 2 loaves of bread. Here is double number line showing varying numbers of customers and the loaves prepared.
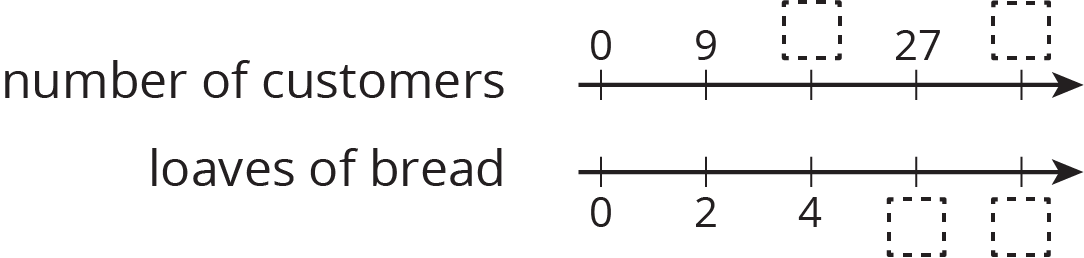
- Complete the missing information.
- The same information is shown on a table. Complete the missing information.
customers loaves row 1 9 2 row 2 4 row 3 27 row 4 14 row 5 1
-
Use either representation to answer these questions.
- How many loaves are needed for 63 customers?
-
How many customers are there if the chef prepares 20 loaves?
- How much of a loaf is prepared for each customer?
Lesson 5
Problem 1
-
Find the product of each number and \frac{1}{100}.
122.1
11.8
1350.1
1.704
- What happens to the decimal point of the original number when you multiply it by \frac{1}{100}? Why do you think that is? Explain your reasoning.
Problem 2
Which expression has the same value as (0.06) \boldcdot (0.154)? Select all that apply.
- 6 \boldcdot \frac{1}{100} \boldcdot 154 \boldcdot \frac{1}{1,000}
- 6 \boldsymbol \boldcdot 154 \boldcdot \frac{1}{100,000}
- 6 \boldcdot (0.1) \boldcdot 154 \boldcdot (0.01)
- 6 \boldsymbol \boldcdot 154 \boldcdot (0.00001)
- 0.00924
Problem 3
Calculate the value of each expression by writing the decimal factors as fractions, then writing their product as a decimal. Show your reasoning.
- (0.01)\boldcdot (0.02)
- (0.3) \boldcdot (0.2)
- (1.2) \boldcdot 5
- (0.9) \boldcdot (1.1)
- (1.5)\boldcdot 2
Problem 4
Problem 5 (from Unit 5, Lesson 3)
Calculate each sum.
- 33.1+ 1.95
- 1.075 + 27.105
- 0.401+9.28
Problem 6 (from Unit 5, Lesson 4)
Calculate each difference. Show your reasoning.
- 13.2 - 1.78
- 23.11 - 0.376
- 0.9 - 0.245
Problem 7 (from Unit 1, Lesson 3)
On the grid, draw a quadrilateral that is not a rectangle that has an area of 18 square units. Show how you know the area is 18 square units.

Lesson 6
Problem 1
Find each product. Show your reasoning.
- (1.2) \boldcdot (0.11)
- (0.34) \boldcdot (0.02)
- 120 \boldcdot (0.002)
Problem 2
You can use a rectangle to represent (0.3) \boldcdot (0.5).
- What must the side length of each square represent for the rectangle to correctly represent (0.3) \boldcdot (0.5)?
- What area is represented by each square?
- What is (0.3) \boldcdot (0.5)? Show your reasoning.

Problem 3
One gallon of gasoline in Buffalo, New York costs $2.29. In Toronto, Canada, one liter of gasoline costs $0.91. There are 3.8 liters in one gallon.
- How much does one gallon of gas cost in Toronto? Round your answer to the nearest cent.
- Is the cost of gas greater in Buffalo or in Toronto? How much greater?
Problem 4 (from Unit 5, Lesson 2)
- 10.3 + 3.7
- 20.99 - 4.97
- 15.99 + 23.51
- 1.893 - 0.353
Problem 5 (from Unit 4, Lesson 11)
Find the value of \frac{49}{50}\div\frac{7}{6} using any method.
Problem 6 (from Unit 1, Lesson 1)
Find the area of the shaded region. All angles are right angles. Show your reasoning.
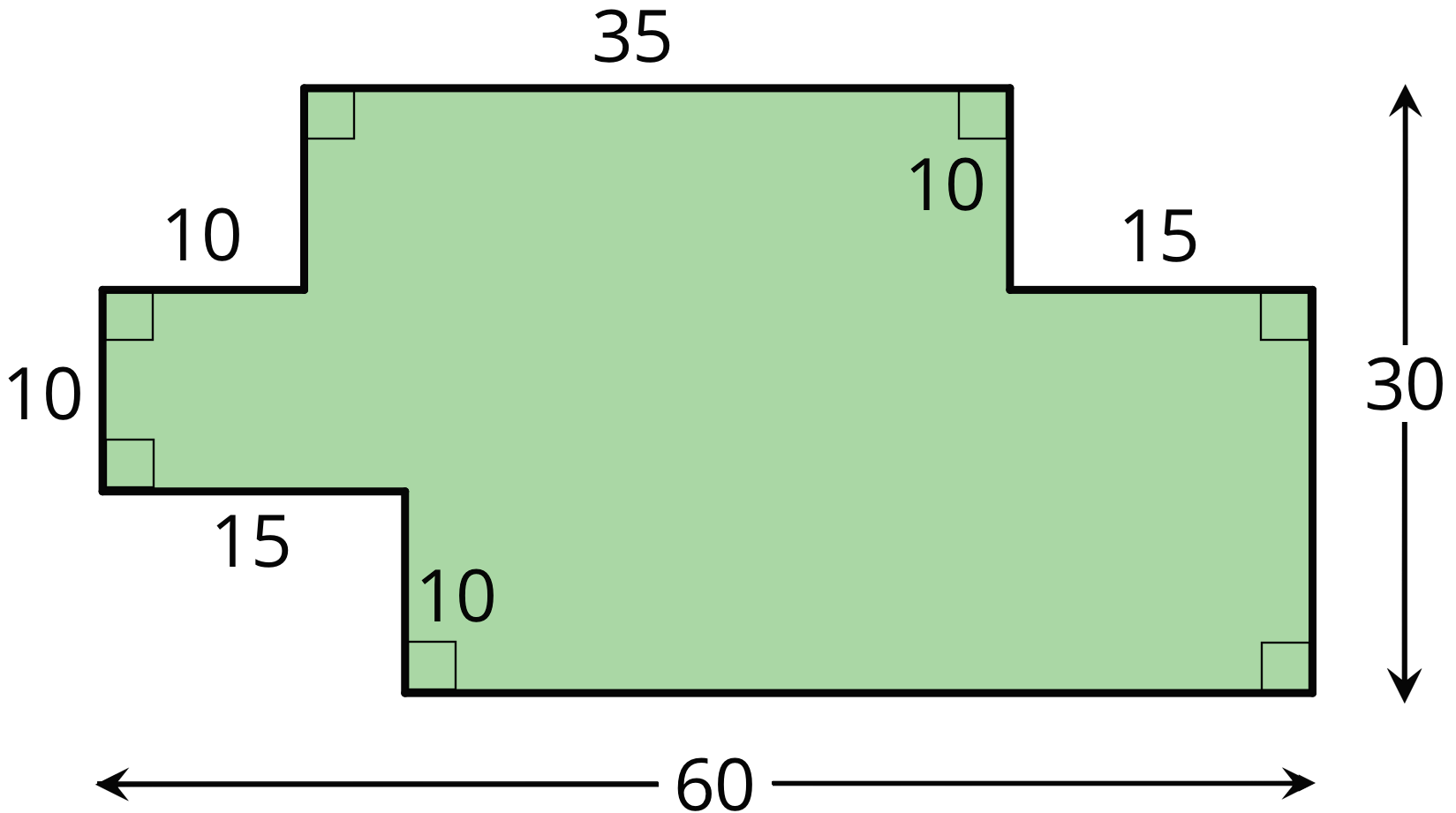
Problem 7
- Priya finds (1.05) \boldcdot (2.8) by calculating 105 \boldcdot 28, then moving the decimal point three places to the left. Why does Priya’s method make sense?
- Use Priya’s method to calculate (1.05) \boldsymbol \boldcdot (2.8). You can use the fact that 105 \boldcdot 28 = 2,\!940.
- Use Priya’s method to calculate (0.0015) \boldcdot (0.024).
Lesson 7
Problem 1
For each expression, choose a sub-rectangle whose area, in square units, matches the expression.
- 3 \boldcdot (0.6)
- (0.4) \boldsymbol \boldcdot 2
- (0.4) \boldcdot (0.6)
- 3 \boldsymbol \boldcdot 2
Problem 2

- Find the areas of sub-rectangles A and B.
- What is the area of the 3.1 by 1.4 rectangle?
Problem 3
Problem 4
Find each product. Show your reasoning.
- (2.5) \boldcdot (1.4)
- (0.64) \boldcdot (0.81)
Problem 5 (from Unit 5, Lesson 3)
Complete the calculations so that each shows the correct sum or difference.

Problem 6 (from Unit 2, Lesson 12)
Diego bought 12 mini muffins for $4.20.
- At this rate, how much would Diego pay for 4 mini muffins?
- How many mini muffins could Diego buy with $3.00? Explain or show your reasoning. If you get stuck, consider using the table.
| number of mini muffins |
price in dollars |
|
|---|---|---|
| row 1 | 12 | 4.20 |
| row 2 | ||
| row 3 | ||
| row 4 |
Lesson 8
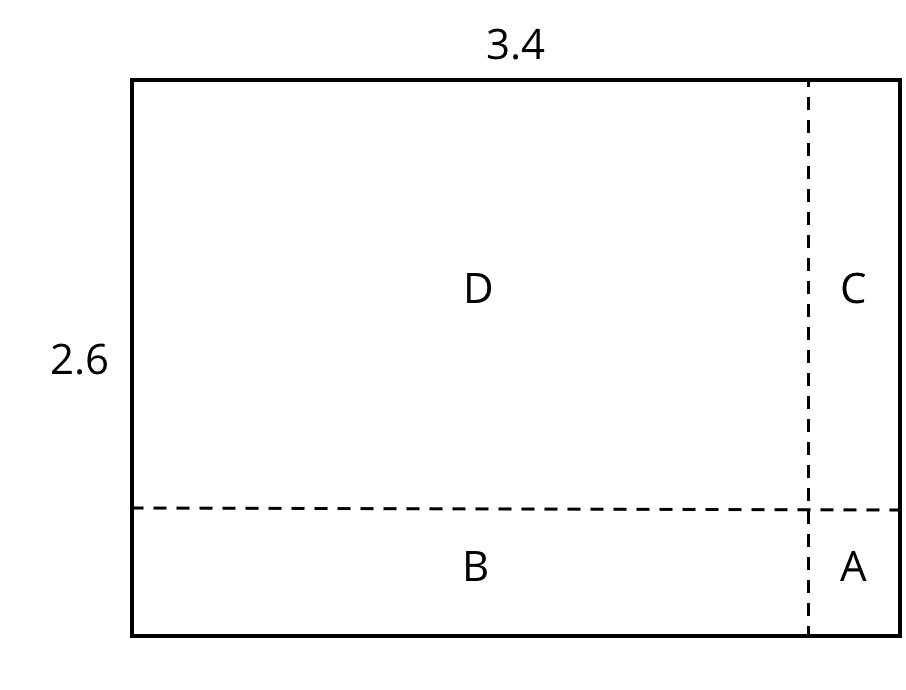
Problem 1
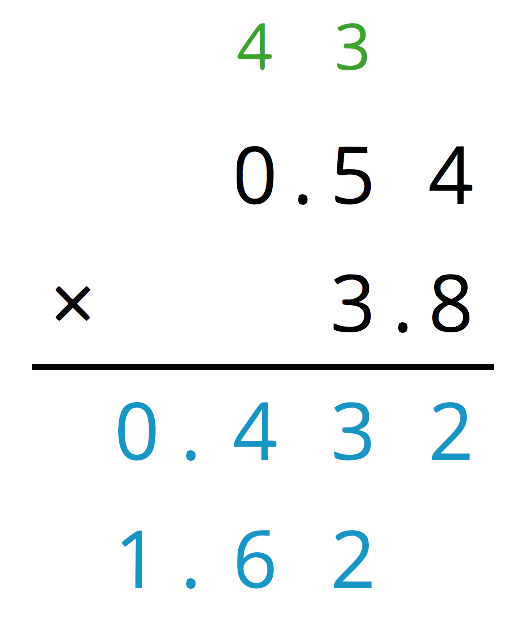

- Which part of the rectangle has an area of 0.432? Which part of the rectangle has an area of 1.62? Show your reasoning.
- What is (0.54) \boldcdot (3.8)?
Problem 2
Explain how the product of 3 and 65 could be used to find (0.03) \boldcdot (0.65).
Problem 3
- (5.4)\boldcdot (2.4)
- (1.67)\boldcdot (3.5)
Problem 4
Problem 5 (from Unit 5, Lesson 3)
Complete the calculations so that each shows the correct sum or difference.
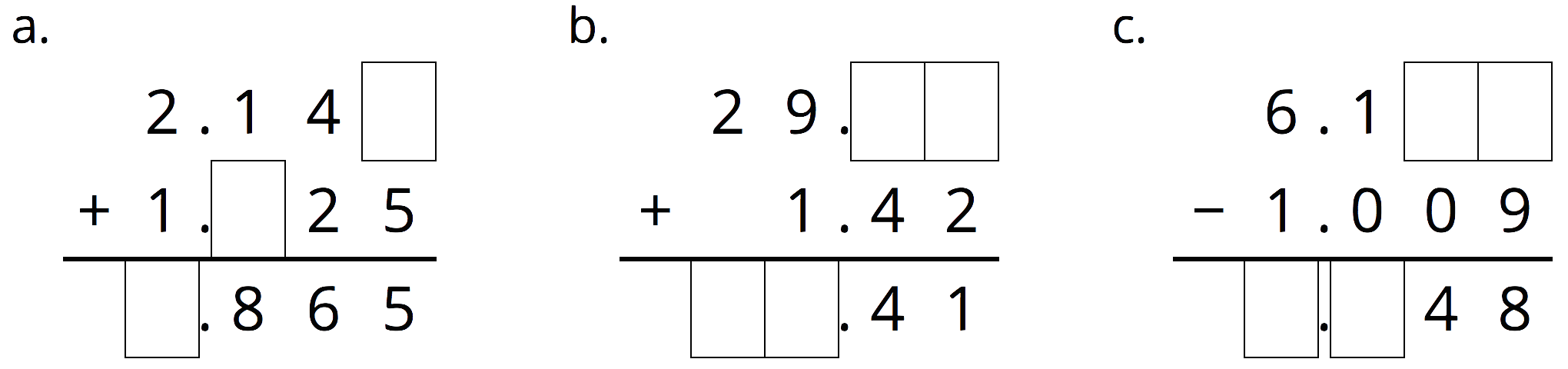
Problem 6 (from Unit 5, Lesson 4)
Which has a greater value: 7.4 - 0.0022 or 7.39-0.0012? Show your reasoning.
Problem 7 (from Unit 2, Lesson 12)
Andre is planting saplings (baby trees). It takes him 30 minutes to plant 3 saplings. If each sapling takes the same amount of time to plant, how long will it take Andre to plant 14 saplings? If you get stuck, consider using the table.
| number of saplings | time in minutes | |
|---|---|---|
| row 1 | 3 | 30 |
| row 2 | 1 | |
| row 3 | 14 |
Lesson 9
Problem 1
Here is one way to find 2,\!105 \div 5 using partial quotients.
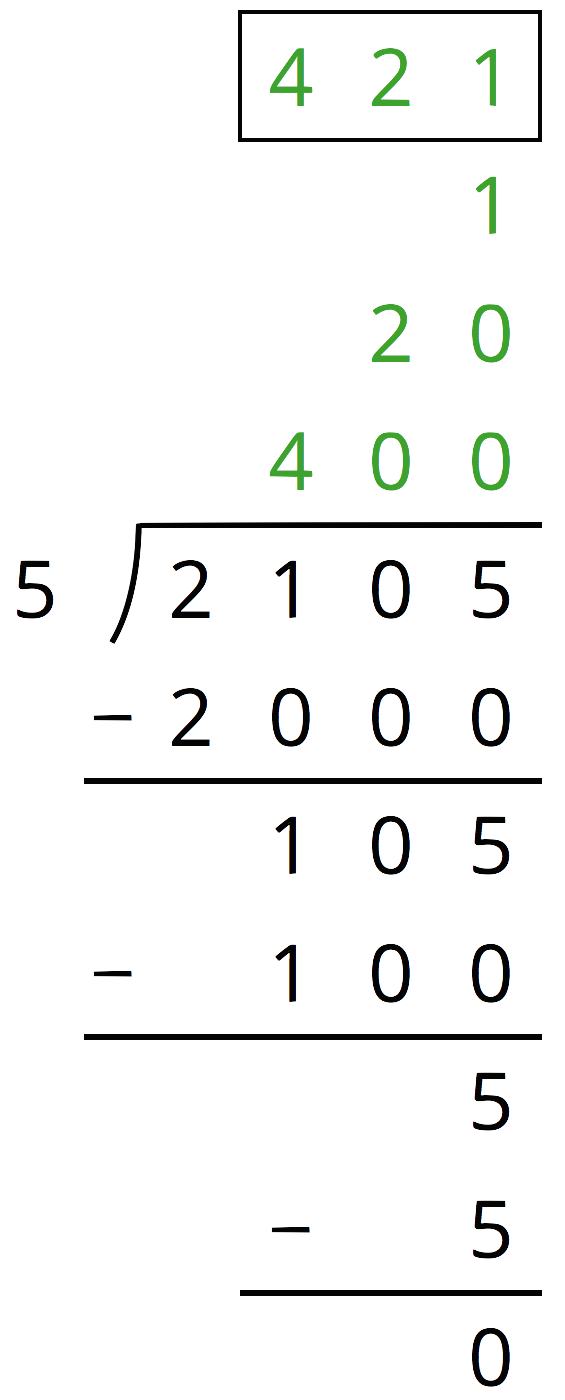
Show a different way of using partial quotients to divide 2,105 by 5.
Problem 2

- How is Jada's work similar to and different from Andre’s work?
- Explain why they have the same answer.
Problem 3
Problem 4
Here is an incomplete calculation of 534\div 6.
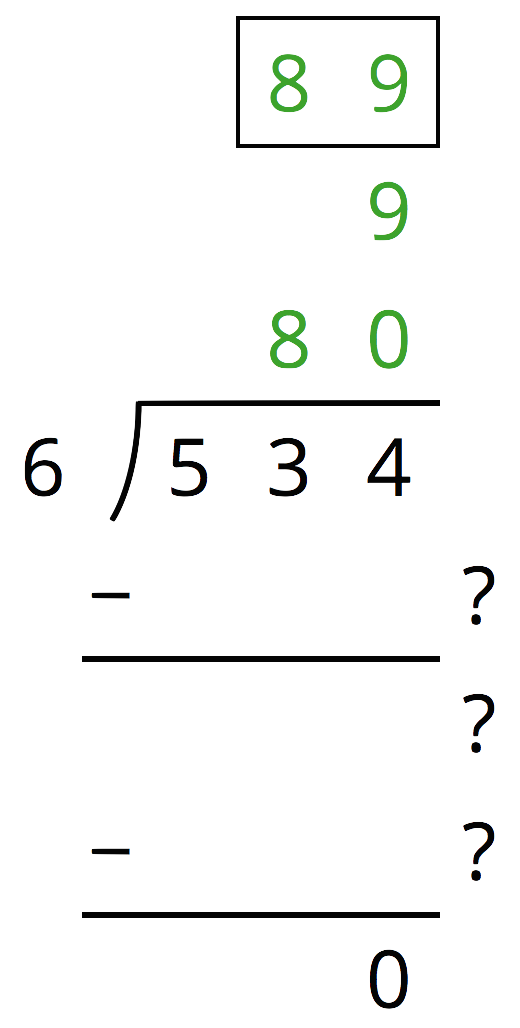
Write the missing numbers (marked with “?”) that would make the calculation complete.
Problem 5
Use the partial quotients method to find 1,\!032 \div 43.
Problem 6 (from Unit 5, Lesson 8)
Which of the polygons has the greatest area?
- A rectangle that is 3.25 inches wide and 6.1 inches long.
- A square with side length of 4.6 inches.
- A parallelogram with a base of 5.875 inches and a height of 3.5 inches.
- A triangle with a base of 7.18 inches and a height of 5.4 inches.
Problem 7 (from Unit 5, Lesson 4)
One micrometer is a millionth of a meter. A certain spider web is 4 micrometers thick. A fiber in a shirt is 1 hundred-thousandth of a meter thick.
- Which is wider, the spider web or the fiber? Explain your reasoning.
- How many meters wider?
Lesson 10
Problem 1
Kiran is using long division to find 623 \div 7.
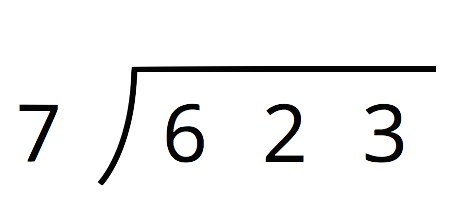
He starts by dividing 62 by 7. In which decimal place should Kiran place the first digit of the quotient (8)?
- Hundreds
- Tens
- Ones
- Tenths
Problem 2
Here is a long-division calculation of 917 \div 7.
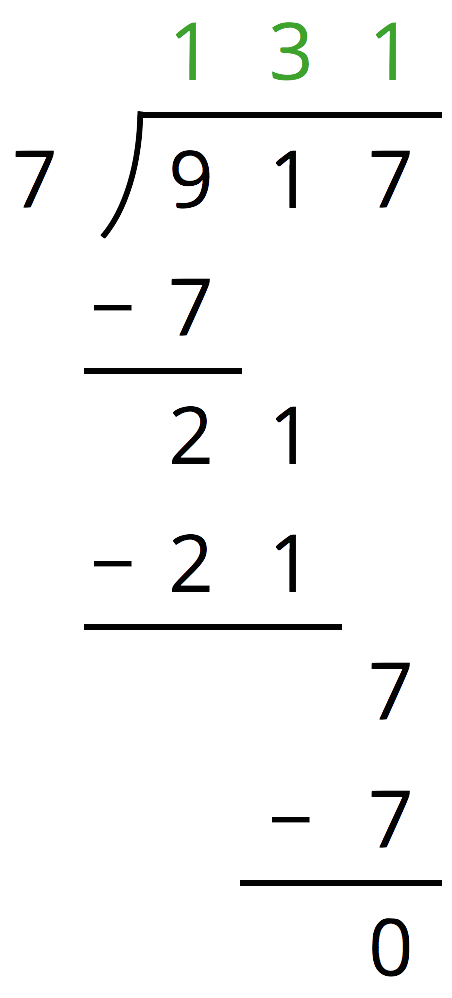
- There is a 7 under the 9 of 917. What does this 7 represent?
- What does the subtraction of 7 from 9 mean?
- Why is a 1 written next to the 2 from 9-7?
Problem 3
Han's calculation of 972 \div 9 is shown here.
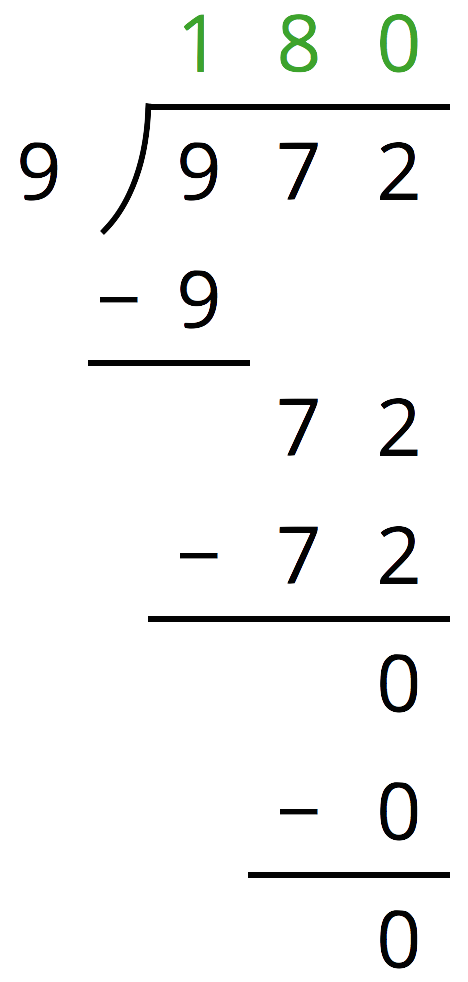
- Find 180 \boldcdot 9.
- Use your calculation of 180 \boldcdot 9 to explain how you know Han has made a mistake.
- Identify and correct Han’s mistake.
Problem 4
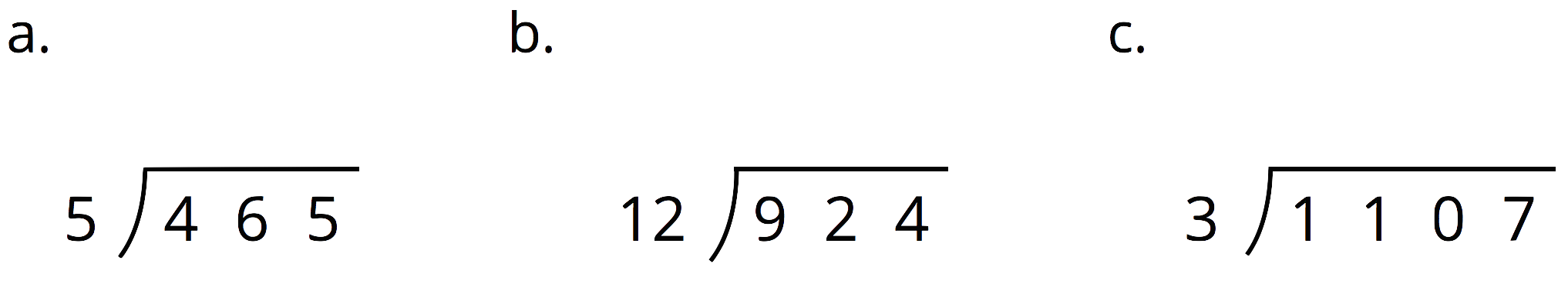
Problem 5 (from Unit 5, Lesson 7)
One ounce of a yogurt contains of 1.2 grams of sugar. How many grams of sugar are in 14.25 ounces of yogurt?
- 0.171 grams
- 1.71 grams
- 17.1 grams
- 171 grams
Problem 6 (from Unit 5, Lesson 4)
The mass of one coin is 16.718 grams. The mass of a second coin is 27.22 grams. How much greater is the mass of the second coin than the first? Show your reasoning.
Lesson 11
Problem 1
Use long division to show that the fraction and decimal in each pair are equal.
-
\frac{3}{4} and 0.75
-
\frac{3}{50} and 0.06
-
\frac{7}{25} and 0.28
Problem 2
Mai walked \frac{1}{8} of a 30-mile walking trail. How many miles did Mai walk? Explain or show your reasoning.
Problem 3
Use long division to find each quotient. Write your answer as a decimal.
-
99\div 12
-
216 \div 5
-
1,\!988 \div 8
Problem 4
To find the decimal of \frac{9}{25}, Tyler reasoned: “\frac{9}{25} is equivalent to \frac{18}{50} and to \frac {36}{100}, so the decimal of \frac{9}{25} is 0.36.”
- Use long division to show that Tyler is correct.
- Is the decimal of \frac{18}{50} also 0.36? Use long division to support your answer.
Problem 5 (from Unit 5, Lesson 4)
Complete the calculations so that each shows the correct difference.
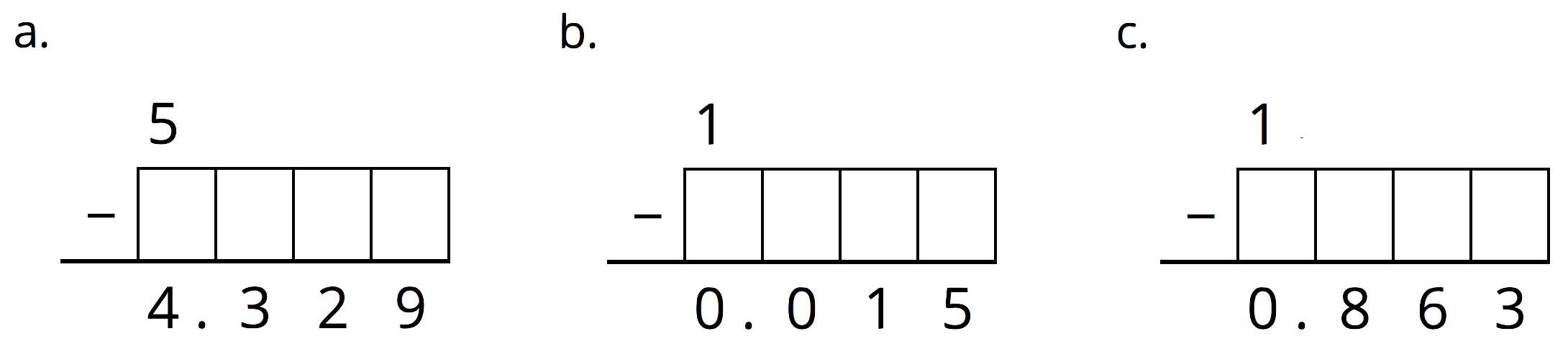
Problem 6 (from Unit 5, Lesson 6)
Use the equation 124 \boldcdot 15 = 1,\!860 and what you know about fractions, decimals, and place value to explain how to place the decimal point when you compute (1.24) \boldcdot (0.15).
Lesson 12
Problem 1
Here is a diagram representing a base-ten number. The large rectangle represents a unit that is 10 times the value of the square. The square represents a unit that is 10 times the value of the small rectangle.

Here is a diagram showing the number being divided into 5 equal groups.
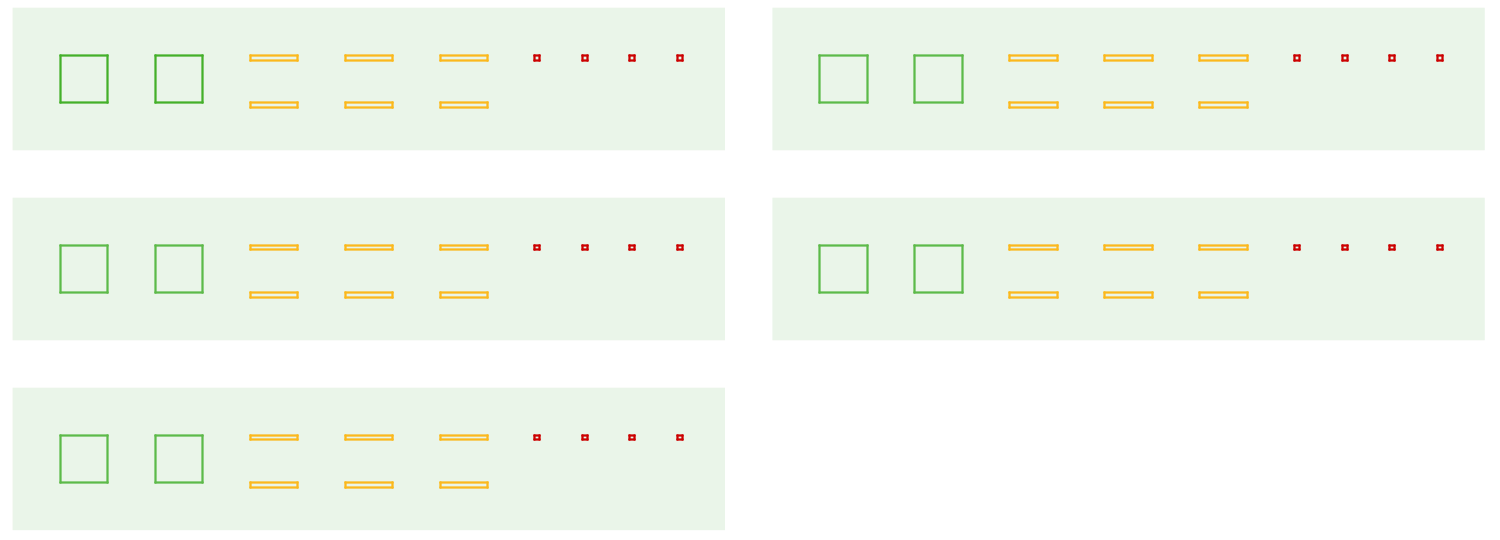
-
If a large rectangle represents 1,000, what division problem did the second diagram show? What is its answer?
-
If a large rectangle represents 100, what division problem did the second diagram show? What is its answer?
-
If a large rectangle represents 10, what division problem did the second diagram show? What is its answer?
Problem 2
-
Explain why all of these expressions have the same value.
4500\div 90
450 \div 9
45 \div 0.9
4.5 \div 0.09
-
What is the common value?
Problem 3
Use long division to find each quotient.
- 7.89 \div 2
- 39.54 \div 3
- 0.176 \div 5
Problem 4
Four students set up a lemonade stand. At the end of the day, their profit is $17.52. How much money do they each have when the profit is split equally? Show or explain your reasoning.
Problem 5 (from Unit 5, Lesson 8)
- A standard sheet of paper in the United States is 11 inches long and 8.5 inches wide. Each inch is 2.54 centimeters. How long and wide is a standard sheet of paper in centimeters?
- A standard sheet of paper in Europe is 21.0 cm wide and 29.7 cm long. Which has the greater area, the standard sheet of paper in the United States or the standard sheet of paper in Europe? Explain your reasoning.
Lesson 13
Problem 1
A student said, “To find the value of 109.2 \div 6, I can divide 1,092 by 60.”
- Do you agree with this statement? Explain your reasoning.
- Calculate the quotient of 109.2 \div 6 using any method of your choice.
Problem 2
Here is how Han found 31.59 \div 13:
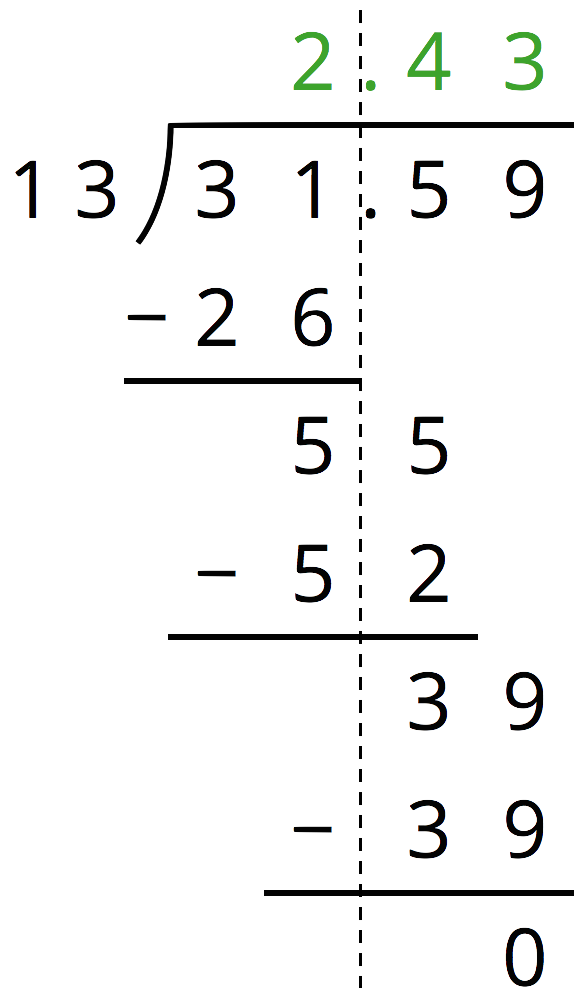
-
At the second step, Han subtracts 52 from 55. How do you know that these numbers represent tenths?
-
At the third step, Han subtracts 39 from 39. How do you know that these numbers represent hundredths?
-
Check that Han’s answer is correct by calculating the product of 2.43 and 13.
Problem 3
- Write two division expressions that have the same value as 61.12 \div 3.2.
- Find the value of 61.12 \div 3.2. Show your reasoning.
Problem 4
A bag of pennies weighs 5.1 kilogram. Each penny weighs 2.5 grams. About how many pennies are in the bag?
- 20
- 200
- 2,000
- 20,000
Problem 5 (from Unit 5, Lesson 3)
Find each difference. If you get stuck, consider drawing a diagram.
- 2.5 - 1.6
- 0.72-0.4
- 11.3-1.75
- 73-1.3
Problem 6 (from Unit 4, Lesson 12)
Plant B is 6\frac23 inches tall. Plant C is 4\frac{4}{15} inches tall. Complete the sentences and show your reasoning.
- Plant C is _______ times as tall as Plant B.
- Plant C is _______ inches ____________ (taller or shorter) than Plant B.
Problem 7 (from Unit 3, Lesson 15)
At a school, 460 of the students walk to school.
- The number of students who take public transit is 20% of the number of students who walk. How many students take public transit?
- The number of students who bike to school is 5% of the number of students who walk. How many students bike to school?
- The number of students who ride the school bus is 110% of the number of students who walk. How many students ride the school bus?
Lesson 14
Problem 1
A roll of ribbon was 12 meters long. Diego cut 9 pieces of ribbon that were 0.4 meter each to tie some presents. He then used the remaining ribbon to make some wreaths. Each wreath required 0.6 meter. For each question, explain your reasoning.
- How many meters of ribbon were available for making wreaths?
- How many wreaths could Diego make with the available ribbon?
Problem 2
The Amazon rainforest covered 6.42 million square kilometers in 1994. In 2014, it covered only \frac{50}{59} as much. Which is closest to the area of the Amazon forest in 2014? Explain how you know without calculating the exact area.
- 6.4 million km2
- 5.4 million km2
- 4.4 million km2
- 3.4 million km2
- 2.4 million km2
Problem 3
| Jada’s points | total points possible | ||
|---|---|---|---|
| row 1 | Homework | 141 | 150 |
| row 2 | Test 1 | 87 | 100 |
| row 3 | Test 2 | 81 | 100 |
| row 4 | Test 3 | 91 | 100 |
- Does Jada have 90% of the total possible points before the final test? Explain how you know.
- Jada thinks that if she gets at least 92 out of 100 on the final test, she will get an A in the class. Do you agree? Explain.
Problem 4 (from Unit 5, Lesson 4)
Find the following differences. Show your reasoning.
- 0.151 - 0.028
- 0.106 - 0.0315
- 3.572 - 2.6014
Problem 5 (from Unit 5, Lesson 13)
Find these quotients. Show your reasoning.
- 24.2 \div 1.1
- 13.25 \div 0.4
- 170.28 \div 0.08
Lesson 15
No practice problems for this lesson.