Lesson 13: Tables and Double Number Line Diagrams

Let’s contrast double number lines and tables.

13.1: Number Talk: Constant Dividend

  1. Find the quotients mentally.

    $150\div 2$

    $150\div 4$

    $150\div 8$

  2. Locate and label the quotients on the number line.
A number line with two tick marks. The numbers 0 and 150 are indicated

13.2: Moving 3,000 Meters

The other day, we saw that Han can run 100 meters in 20 seconds.

Han wonders how long it would take him to run 3,000 meters at this rate. He made a table of equivalent ratios.

  1. Do you agree that this table represents the situation? Explain your reasoning.
row 1 20 100
row 2 10 50
row 3 1 5
row 4 3,000  
  1. Complete the last row with the missing number.
  1. What question about the situation does this number answer?
  1. What could Han do to improve his table?
  1. Priya can bike 150 meters in 20 seconds. At this rate, how long would it take her to bike 3,000 meters?
                       
    row 1    
    row 2    
    row 3    
    row 4    
    row 5    

  1. Priya’s neighbor has a dirt bike that can go 360 meters in 15 seconds. At this rate, how long would it take them to ride 3,000 meters?

13.3: The International Space Station

The International Space Station orbits around the Earth at a constant speed. Your teacher will give you either a double number line or a table that represents this situation. Your partner will get the other representation.

  1. Complete the parts of your representation that you can figure out for sure.
  2. Share information with your partner, and use the information that your partner shares to complete your representation.
International Space Station Copyright Owner: NASA License: Public Domain Via: NASA
  1. What is the speed of the International Space Station?
  2. Place the two completed representations side by side. Discuss with your partner some ways in which they are the same and some ways in which they are different.
  3. Record at least one way that they are the same and one way they are different.

Summary

On a double number line diagram, we put labels in front of each line to tell what the numbers represent. On a table, we put labels at the top of each column to tell what the numbers represent.

Here are two different ways we can represent the situation: “A snail is moving at a constant speed down a sidewalk, traveling 6 centimeters per minute.”

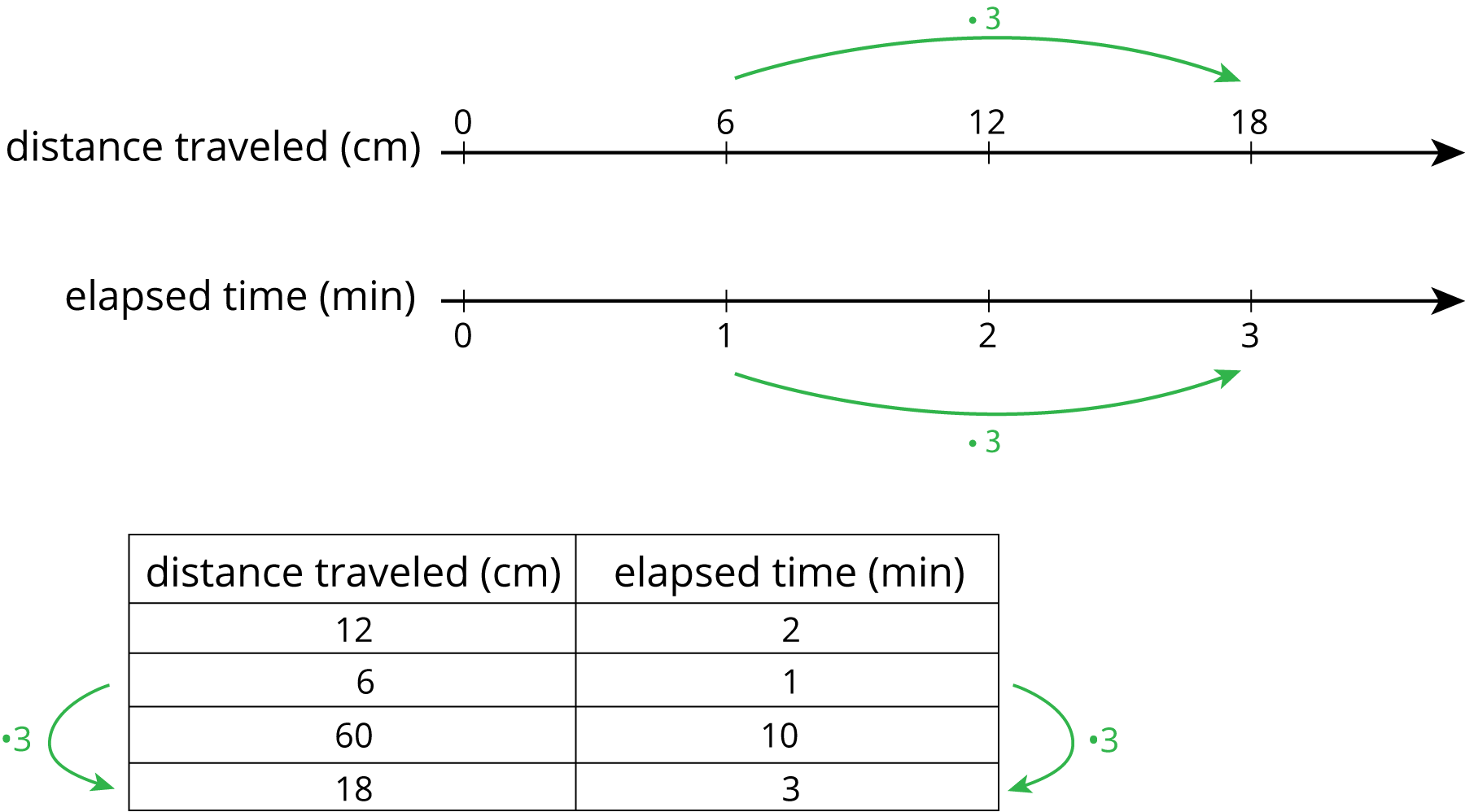
A double number line with 4 evenly spaced tick marks. For "distance traveled, in centimeters" the numbers 0, 6, 12, and 18 are indicated and an arrow labeled "times 3" is drawn from 6 to 18 . For "elapsed time, in minutes" the numbers 0, 1, 2, and 3 are indicated and an arrow labeled "times 3" is drawn from 1 to 3. A 2-column table with 4 rows of data. The first column is labeled "distance traveled, in centimeters" and the second column is labeled "elapsed time, in minutes." Row 1: 12, 2; Row 2: 6, 1; Row 3: 60, 10; Row 4: 18, 3.
 

Both double number lines and tables can help us use multiplication to make equivalent ratios, but there is an important difference between the two representations.

On a double number line, the numbers on each line are listed in order. With a table, you can write the ratios in any order. For this reason, sometimes a table is easier to use to solve a problem.

For example, what if we wanted to know how far the snail travels in 10 minutes? Notice that 60 centimeters in 10 minutes is shown on the table, but there is not enough room for this information on the double number line.

Practice Problems ▶