Equations are very useful for solving problems with constant speeds. Here is an example.
A boat is traveling at a constant speed of 25 miles per hour.
- How far can the boat travel in 3.25 hours?
- How long does it take for the boat to travel 60 miles?
We can write equations to help us answer questions like these. Let's use $t$ to represent the time in hours and $d$ to represent the distance in miles that the boat travels.
-
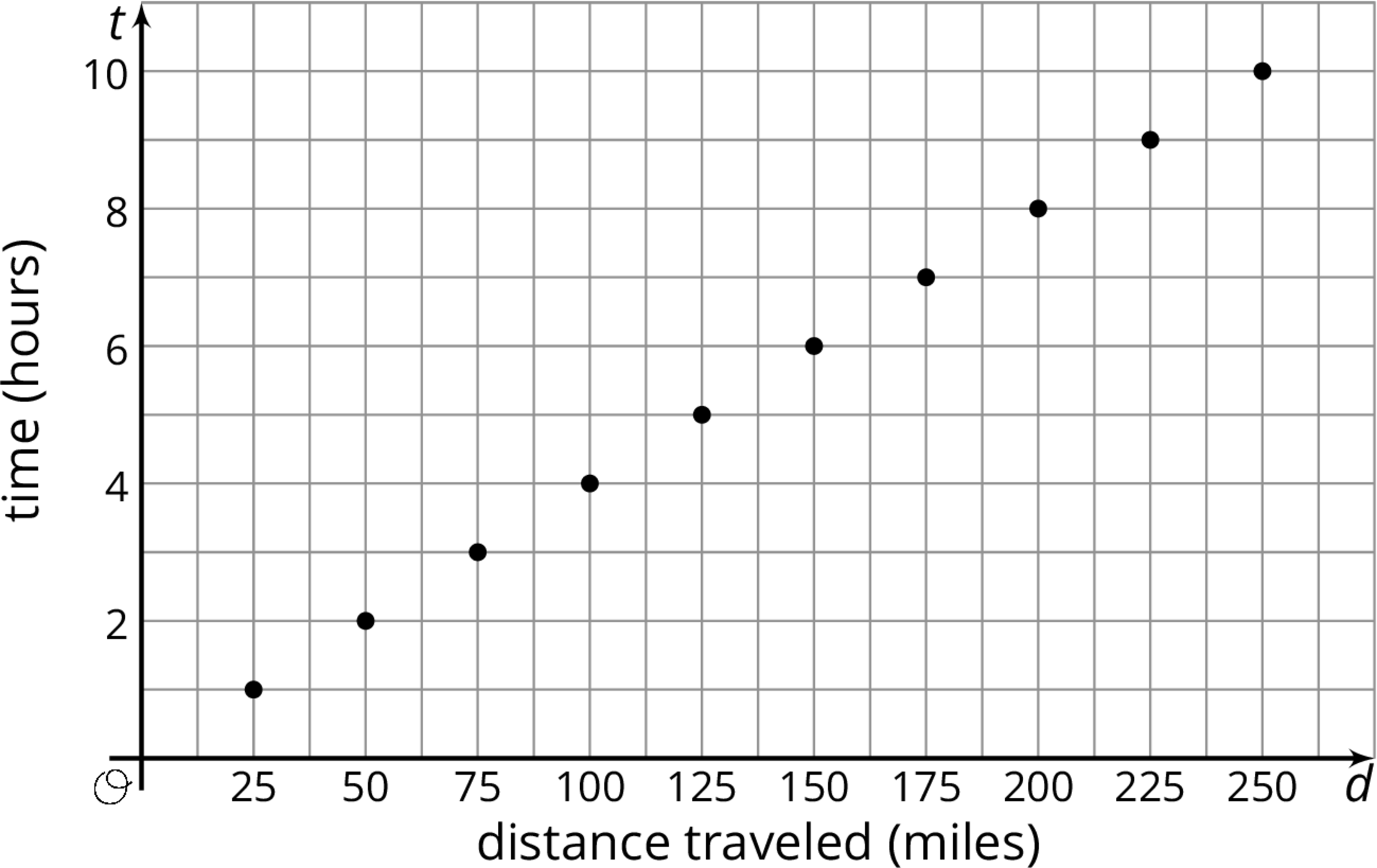
When we know the time and want to find the distance, we can write: $$d = 25t$$
In this equation, if $t$ changes, $d$ is affected by the change, so we $t$ is the independent variable and $d$ is the dependent variable.
This equation can help us find $d$ when we have any value of $t$. In $3.25$ hours, the boat can travel $25(3.25)$ or $81.25$ miles.
-
When we know the distance and want to find the time, we can write: $$t = \frac{d}{25}$$ In this equation, if $d$ changes, $t$ is affected by the change, so we $d$ is the independent variable and $t$ is the dependent variable.
This equation can help us find $t$ when for any value of $d$. To travel 60 miles, it will take $\frac{60}{25}$ or $2 \frac{2}{5}$ hours.
These problems can also be solved using important ratio techniques such as a table of equivalent ratios. The equations are particularly valuable in this case because the answers are not round numbers or easy to quickly evaluate.
We can also graph the two equations we wrote to get a visual picture of the relationship between the two quantities: