Lesson 14: Fractional Lengths in Triangles and Prisms

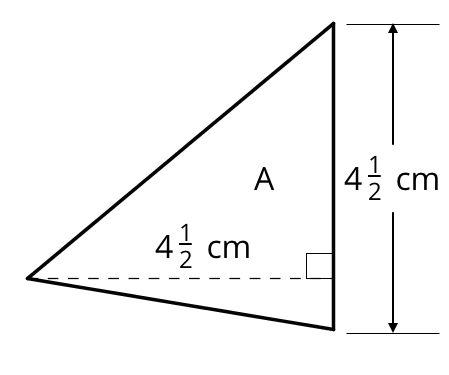
Let’s explore area and volume when fractions are involved.

14.1: Area of Triangle

Find the area of Triangle A in square centimeters. Show your reasoning.

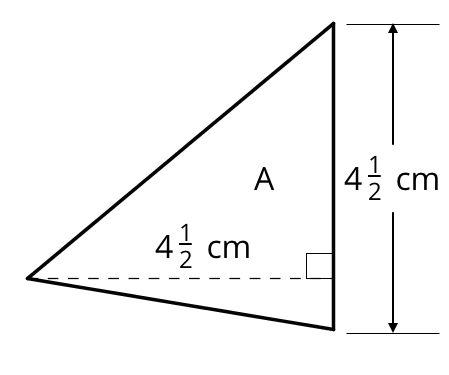
A triangle labeled A is drawn such that one vertex is to the left, one vertex is above the first vertex and to right, and the third vertex is below the first and directly below the second vertex. The vertical side of the triangle is labeled 4 and one half centimeters. A dashed line from the first vertex to the vertical side of the triangle is drawn and a right angle symbol is indicated. The dashed line is labeled 4 and one half centimeters.

14.2: Bases and Heights of Triangles

  1. The area of Triangle B is 8 square units. Find the length of $b$. Show your reasoning.
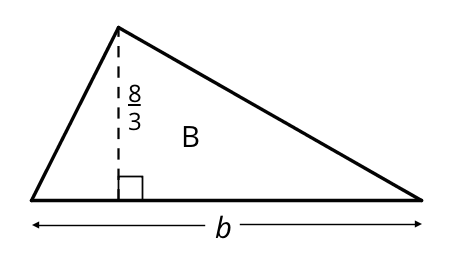
    A triangle labeled B has a horizontal side on the bottom of the triangle and a vertex above the horizontal side. A dashed line from the vertex to the horizontal side is drawn and a right angle symbol is indicated. The horizontal side is labeled b and the dashed line is labeled eight thirds.

     

  2. The area of Triangle C is $\frac{54}{5}$ square units. What is the length of $h$? Show your reasoning.
    A triangle labeled C has a horizontal side at the top of the triangle and a vertex below the horizontal side and to the left. A horizontal line extends from the horizontal side and to the left. A dashed line is drawn from the bottom vertex to the extended horizontal line and a right angle symbol is indicated. The dashed line is labeled h and the horizontal side of the triangle is labeled 3 and three fifths.

     

14.3: Volumes of Cubes and Prisms

Use the cubes or the applet for the following questions. 

GeoGebra Applet fK74qEqW

  1. Your teacher will give you a set of cubes with an edge length of $\frac12$ inch. Use them to help you answer the following questions.

    1. Here is a drawing of a cube with an edge length of 1 inch. How many cubes with an edge length of $\frac12$ inch are needed to fill this cube?

       

    2. What is the volume, in cubic inches, of a cube with an edge length of $\frac12$ inch? Explain or show your reasoning.

    3. Four cubes are piled in a single stack to make a prism. Each cube has an edge length of $\frac12$ inch. Sketch the prism, and find its volume in cubic inches.

  2. Use cubes with an edge length of $\frac12$ inch to build prisms with the lengths, widths, and heights shown in the table.

    1. For each prism, record in the table how many $\frac12$-inch cubes can be packed into the prism and the volume of the prism.

        prism
      length (in)      		 prism
      width (in)      		 prism
      height (in)      		 number of $\frac12$-inch
      cubes in prism      		 volume of
      prism (cu in)
      row 1 $\frac12$ $\frac12$ $\frac12$    
      row 2 1 1 $\frac12$    
      row 3 2 1 $\frac12$    
      row 4 2 2 1    
      row 5 4 2 $\frac32$    
      row 6 5 4 2    
      row 7 5 4 $2\frac12$    
    2. Analyze the values in the table. What do you notice about the relationship between the edge lengths of each prism and its volume?
  3. What is the volume of a rectangular prism that is $1\frac12$ inches by $2\frac14$ inches by 4 inches? Show your reasoning.

Summary

If a rectangular prism has edge lengths of 2 units, 3 units, and 5 units, we can think of it as 2 layers of unit cubes, with each layer having $(3 \boldcdot 5)$ unit cubes in it. So the volume, in cubic units, is: $$2\boldcdot 3\boldcdot 5$$

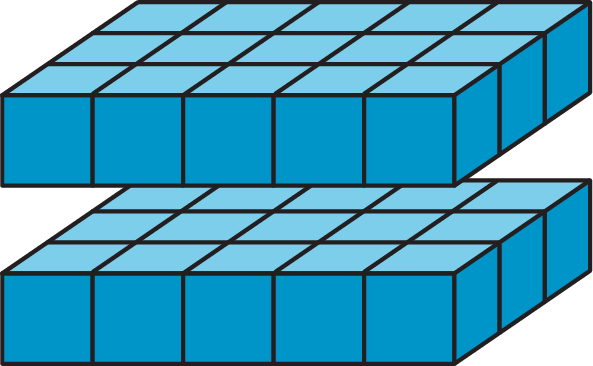
Two layers of unit cubes. Each layer has edge lengths of 1 unit, 3 units, and 5 units. The figure is labeled 2 times 3 times 5.

To find the volume of a rectangular prism with fractional edge lengths, we can think of it as being built of cubes that have a unit fraction for their edge length. For instance, if we build a prism that is $\frac12$-inch tall, $\frac32$-inch wide, and 4 inches long using cubes with a $\frac12$-inch edge length, we would have:

  • A height of 1 cube, because $1 \boldcdot \frac 12 = \frac12$
  • A width of 3 cubes, because $3 \boldcdot \frac 12 = \frac32$
  • A length of 8 cubes, because $8 \boldcdot \frac 12 = 4$

The volume of the prism would be $1 \boldcdot 3 \boldcdot 8$, or 24 cubic units. How do we find its volume in cubic inches?

We know that each cube with a $\frac12$-inch edge length has a volume of $\frac 18$ cubic inch, because $\frac 12 \boldcdot \frac 12 \boldcdot \frac 12 = \frac18$. Since the prism is built using 24 of these cubes, its volume, in cubic inches, would then be $24 \boldcdot \frac 18$, or 3 cubic inches.  

The volume of the prism, in cubic inches, can also be found by multiplying the fractional edge lengths in inches: $$ \frac 12 \boldcdot  \frac 32 \boldcdot 4 = 3$$

Practice Problems ▶