Lesson 10: Dividing by Unit and Non-Unit Fractions

Let’s look for patterns when we divide by a fraction.

10.1: Dividing by a Whole Number

Work with a partner. One person should solve the problems labeled “Partner A,” and the other should solve those labeled “Partner B.” Write an equation for each question. If you get stuck, draw a diagram.

  1. Partner A

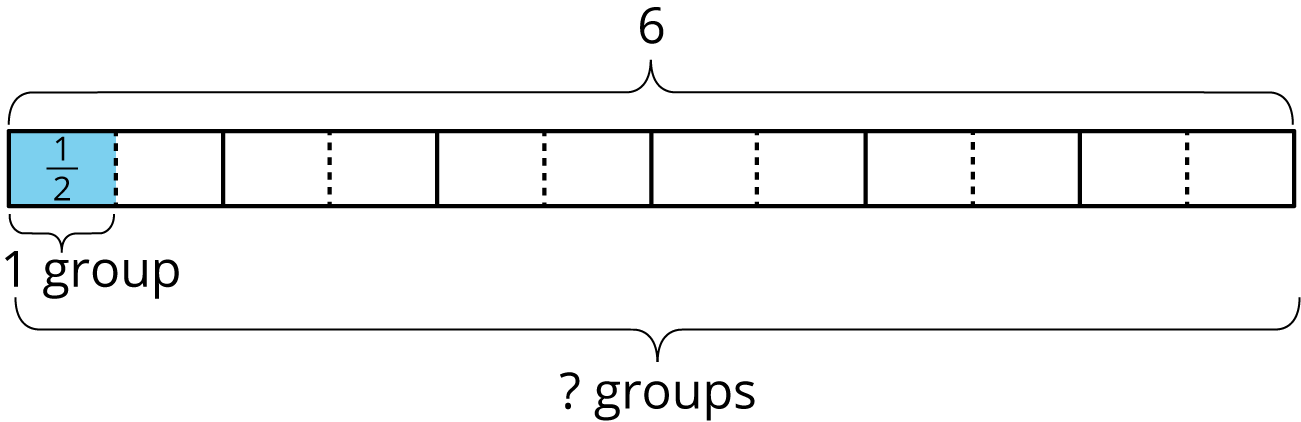
    1. How many 3s are in 12?

      Division equation:

    A blank grid with height 5 units and length 16 units.

    1. How many 4s are in 12?

      Division equation:

    A blank grid with height 5 units and length 16 units.

    1. How many 6s are in 12?

      Division equation:

    A blank grid with height 5 units and length 16 units.

  2. Partner B

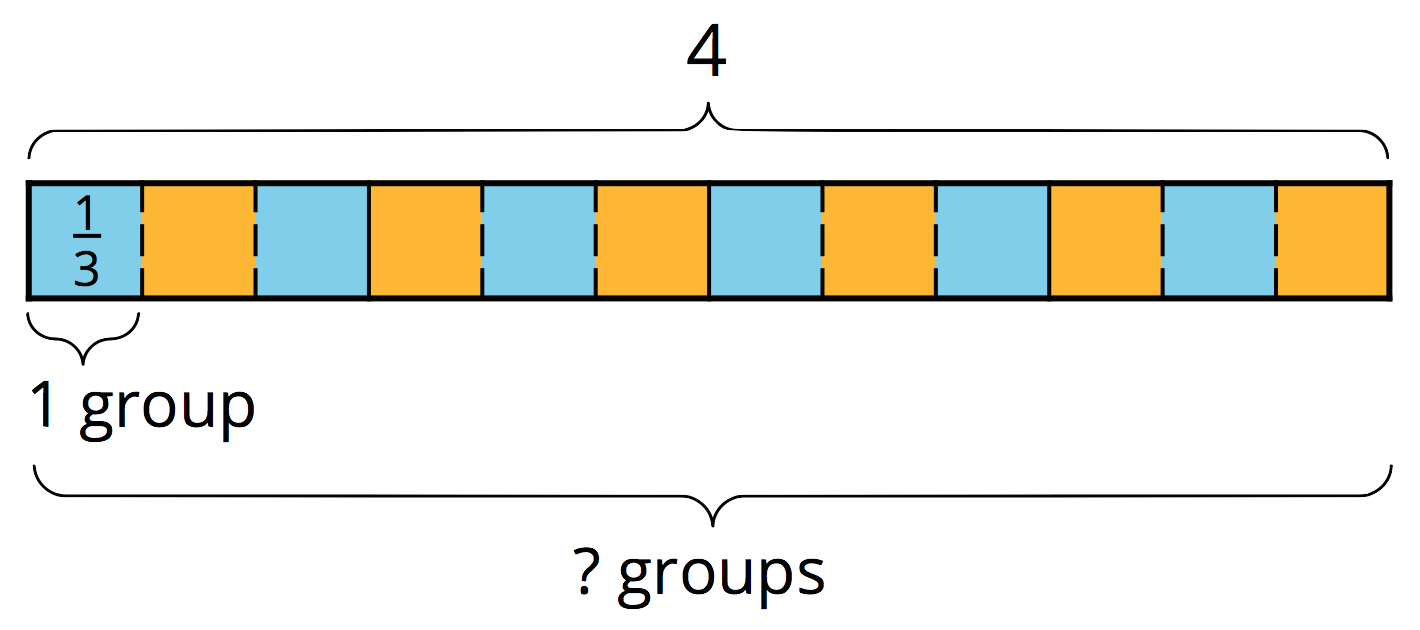
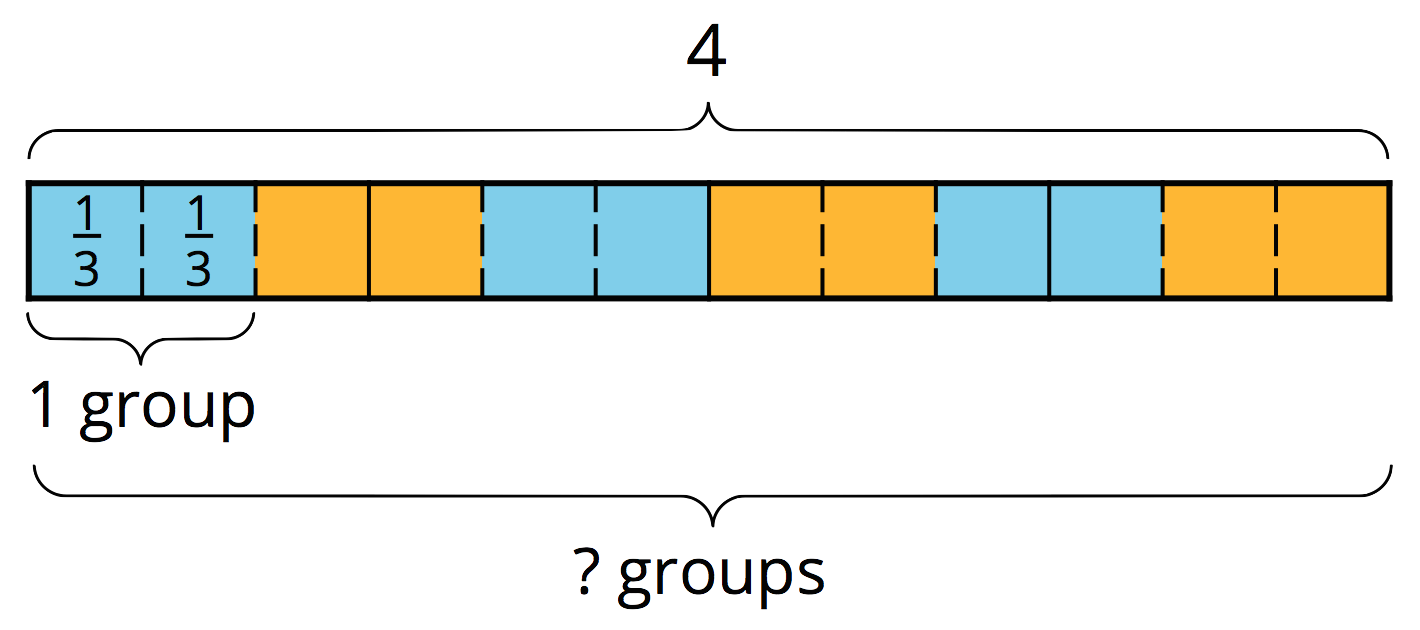
    1. What is 12 groups of $\frac 13$?

      Multiplication equation:

    A blank grid with height 5 units and length 16 units.

    1. What is 12 groups of $\frac 14$?

      Multiplication equation:

    A blank grid with height 5 units and length 16 units.

    1. What is 12 groups of $\frac 16$?

      Multiplication equation:

    A blank grid with height 5 units and length 16 units.

  3. What do you notice in the diagrams and equations? Discuss with your partner.

  4. Complete this sentence based on your observations: Dividing by a whole number $a$ produces the same result as multiplying by _____________ .

10.2: Dividing by Unit Fractions

  1. To find the value of $6 \div \frac 12$, Elena thought, “How many $\frac 12$s are in 6?” and drew a tape diagram. It shows 6 ones with each one partitioned into 2 equal pieces.

    $6 \div \frac 12$

    For each division expression, complete the diagram using the same interpretation of division as Elena’s. Then, write the value of the expression. Think about how to find that value without counting the pieces in the diagram.

    a. $6 \div \frac 13$

    A tape diagram of 6 equal parts. From the beginning of the diagram to the end of the diagram a brace is drawn and is labeled 6.

    Value of the expression: ____________

    b. $6 \div \frac 14$

    A tape diagram of 6 equal parts. From the beginning of the diagram to the end of the diagram a brace is drawn and is labeled 6.

    Value of the expression: ____________

    c. $6 \div \frac 16$

    A tape diagram of 6 equal parts. From the beginning of the diagram to the end of the diagram a brace is drawn and is labeled 6.

    Value of the expression: ____________

  2. Analyze the expressions and your answers. Look for a pattern. How did you find how many $\frac 12$s, $\frac 13$s, $\frac 14$s, or $\frac 16$s were in 6 without counting? Explain your reasoning.

  3. Use your observations from previous questions to find the values of the following expressions. If you get stuck, you can draw diagrams.

    1. $6 \div \frac 18$
    2. $6 \div \frac {1}{10}$
    1. $6 \div \frac {1}{25}$
    2. $6 \div \frac {1}{b}$

  4. Find the value of each expression.

    1. $8 \div \frac 14$
    2. $12 \div \frac 15$
    1. $a \div \frac 12$
    2. $a \div \frac {1}{b}$

10.3: Dividing by Non-unit Fractions

  1. To find the value of $6 \div \frac 23$, Elena began by drawing her diagram in the same way she did for $6 \div \frac 13$.

    1. Use her diagram to find out how many $\frac 23$s are in 6. Adjust and label the diagram as needed.
    2. She says, “To find $6 \div \frac23$, I can just take the value of $6 \div \frac13$ then either multiply it by $\frac 12$ or divide it by 2.” Do you agree with her? Explain why or why not.

  2. For each division expression, complete the diagram using the same interpretation of division that Elena did. Then, write the value of the expression. Think about how you could find the value of each expression without counting the equal pieces in your diagram.

    $6 \div \frac 34$

    Value of the expression:___________

    $6 \div \frac 43$

    Value of the expression:___________

    $6 \div \frac 46$

     Value of the expression:___________

  3. Elena studied her diagrams and noticed that she always took the same two steps to represent division by a fraction on a tape diagram. She said:

    “My first step was to partition each 1 whole into as many parts as the number in the denominator. So if the expression is $6 \div \frac 34$, I would partition each 1 whole into 4 parts. Now I have 4 times as many parts.

    My second step was to put a certain number of those parts into one group, and that number is the numerator of the divisor. So if the fraction is $\frac34$, I would put 3 of the $\frac 14$s into one group. I could then tell how many $\frac 34$s are in 6.”

    Which expression represents how many $\frac 34$s Elena would have after these two steps? Be prepared to explain your reasoning.

    1. $6 \div 4 \boldcdot 3$
    2. $6 \div 4 \div 3$
    1. $6 \boldcdot 4 \div 3$
    2. $6 \boldcdot 4 \boldcdot 3$

  4. Use your work from the previous questions to find the values of the following expressions. Draw diagrams if you are stuck.

    a. $6 \div \frac27$

    b. $6\div\frac{3}{10}$

    c. $6 \div \frac {6}{25}$

Summary

To answer the question “How many $\frac 13$s are in 4?” or “What is $4 \div \frac 13$?”, we can reason that there are 3 thirds in 1, so there are $(4\boldcdot 3)$ thirds in 4.

In other words, dividing 4 by $\frac13$ has the same outcome as multiplying 4 by 3. 

$$4\div \frac13 = 4 \boldcdot 3$$

In general, dividing a number by a unit fraction $\frac{1}{b}$ is the same as multiplying the number by $b$, which is the reciprocal of $\frac{1}{b}$.

How can we reason about $4 \div \frac23$?

We already know that there are $(4\boldcdot 3)$ or 12 groups of $\frac 13$s in 4. To find how many $\frac23$s are in 4, we need to put together every 2 of the $\frac13$s into a group. Doing this results in half as many groups, which is 6 groups. In other words:

$$4 \div \frac23 = (4 \boldcdot 3) \div 2$$

or

$$4 \div \frac23 = (4 \boldcdot 3) \boldcdot \frac 12$$

In general, dividing a number by $\frac{a}{b}$, is the same as multiplying the number by $b$ and then dividing by $a$, or multiplying the number by $b$ and then by $\frac{1}{a}$.

Practice Problems ▶