Lesson 11: Dividing Numbers that Result in Decimals

Let’s find quotients that are not whole numbers.

11.1: Number Talk: Evaluating Quotients

Find the quotients mentally.

$400\div8$

$80\div8$

$16\div8$

$496\div8$

11.2: Keep Dividing

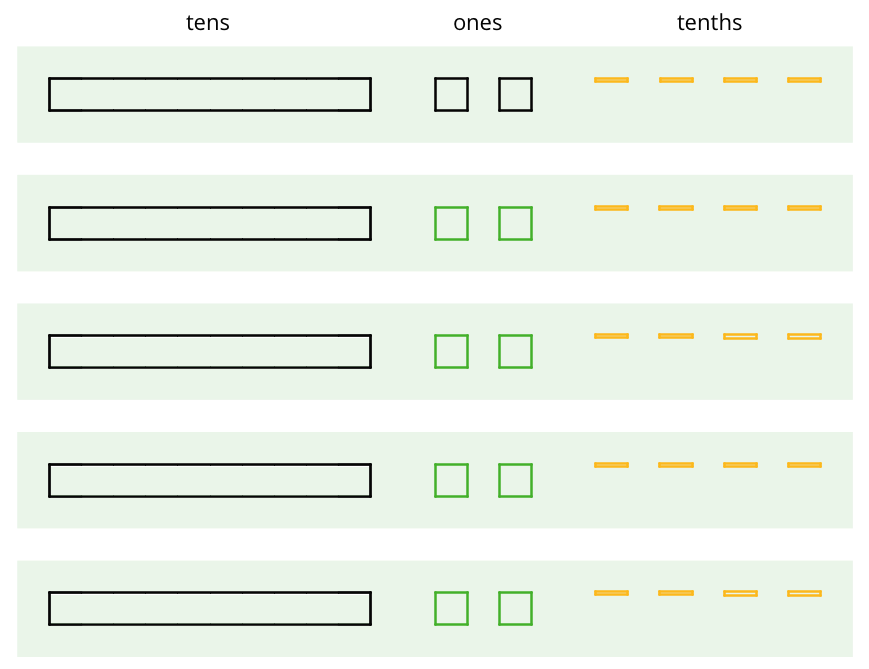
Here is how Mai used base-ten diagrams to calculate $62 \div 5$.

She started by representing 62. 

She then made 5 groups, each with 1 ten. There was 1 ten left. She unbundled it into 10 ones and distributed the ones across the 5 groups.

Here is her diagram for $62 \div 5$.

  1. Discuss these questions with a partner and write down your answers:

    1. Mai should have a total of 12 ones, but her diagram shows only 10. Why?
    2. She did not originally have tenths, but in her diagram each group has 4 tenths. Why?
    3. What value has Mai found for $62 \div 5$? Explain your reasoning.
  2. Find the quotient of $511 \div 5$ by drawing base-ten diagrams or by using the partial quotients method. Show your reasoning. If you get stuck, work with your partner to find a solution.
  3. Four students share a \$271 prize from a science competition. How much does each student get if the prize is shared equally? Show your reasoning.

11.3: Using Long Division to Calculate Quotients

  1. Here is how Lin calculated $62 \div 5$.

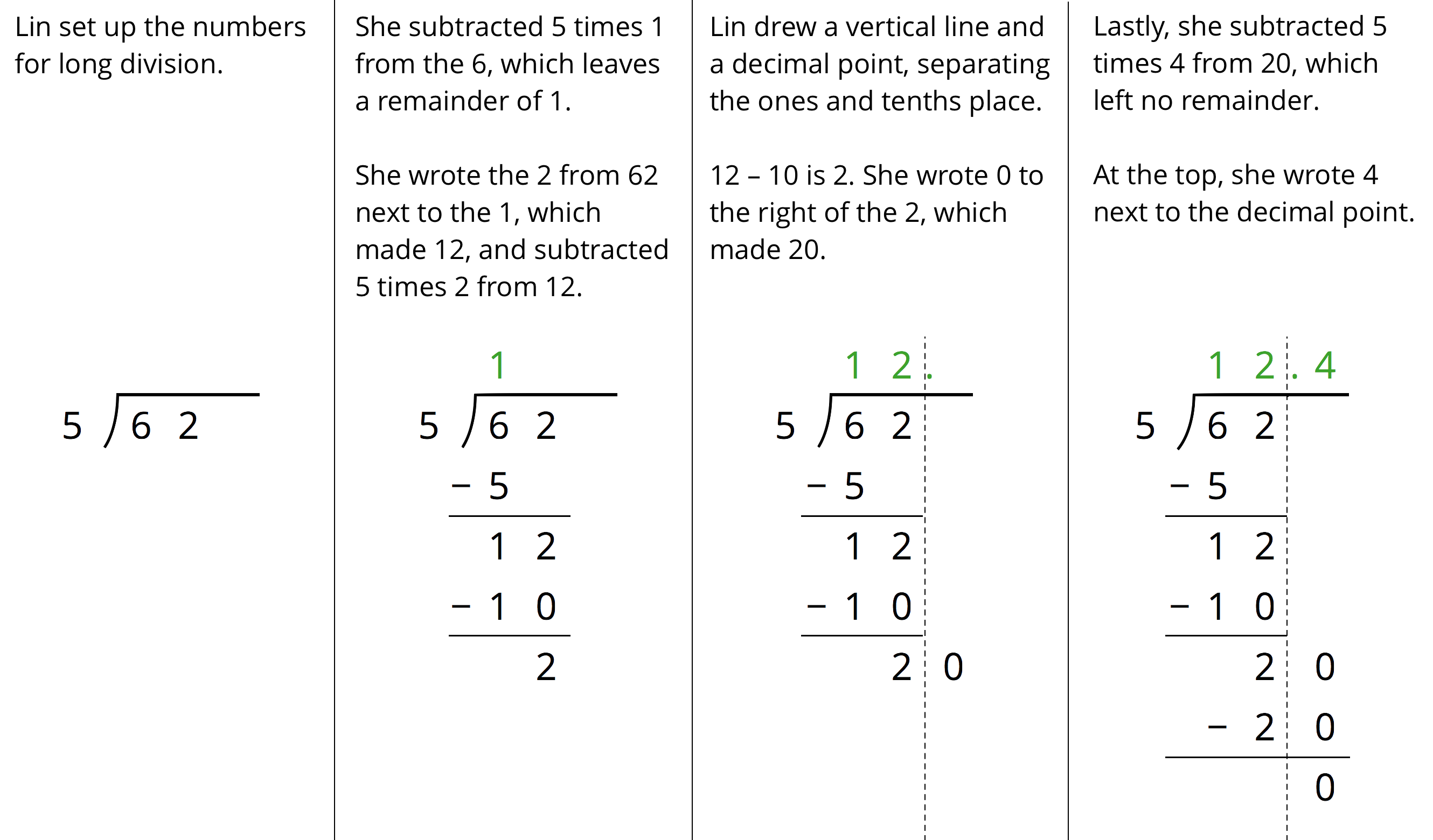
    Discuss with your partner:

    • Lin put a 0 after the remainder of 2. Why? Why does this 0 not change the value of the quotient?

    • Lin subtracted 5 groups of 4 from 20. What value does the 4 in the quotient represent?

    • What value did Lin find for $62 \div 5$?

  2. Use long division to find the value of each expression. Then pause so your teacher can review your work.

    1. $126 \div 8$  
    1. $90 \div 12$

  3. Use long division to show that:

    1. $5 \div 4$, or $\frac 54$, is 1.25.
    2. $4 \div 5$, or $\frac 45$, is 0.8.
    1. $1 \div 8$, or $\frac 18$, is 0.125.
    2. $1 \div 25$, or $\frac {1}{25}$, is 0.04.

  4. Noah said we cannot use long division to calculate $10 \div 3$ because there will always be a remainder.

    1. What do you think Noah meant by “there will always be a remainder”?
    2. Do you agree with his statement? Why or why not?

Summary

Dividing a whole number by another whole number does not always produce a whole-number quotient. Let’s look at $86 \div 4$, which we can think of as dividing 86 into 4 equal groups. 

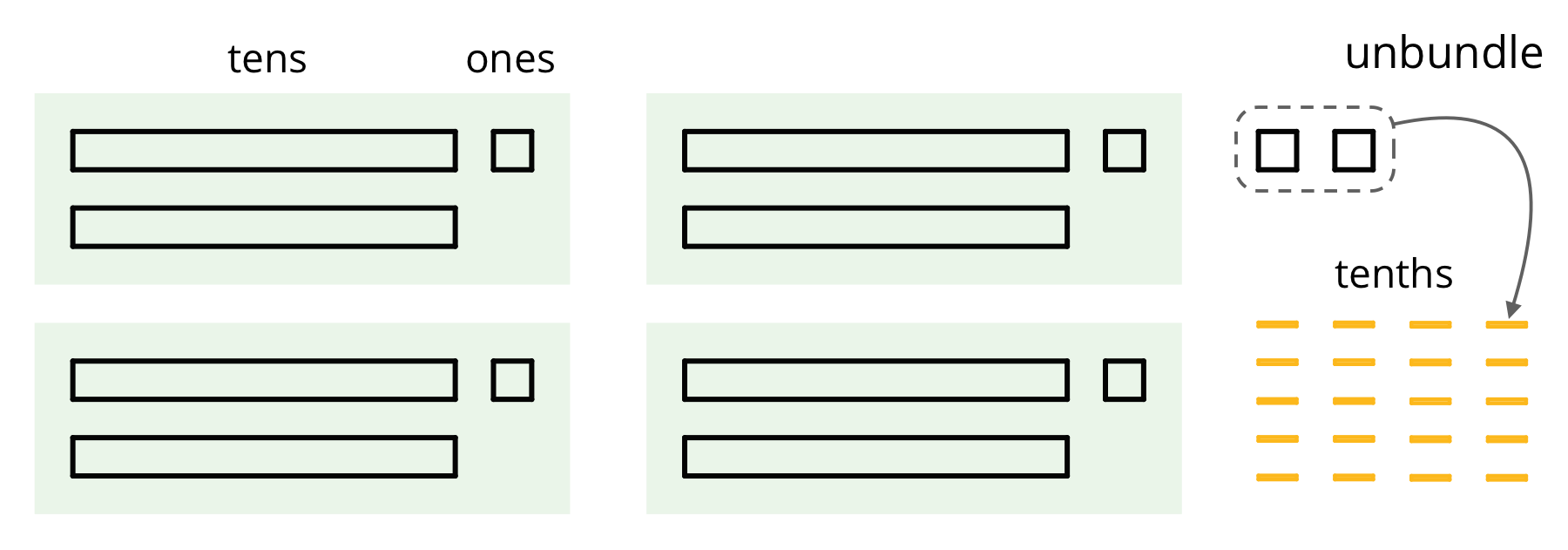
We can see in the base-ten diagram that there are 4 groups of 21 in 86 with 2 ones left over. To find the quotient, we need to distribute the 2 ones into the 4 groups. To do this, we can unbundle or decompose the 2 ones into 20 tenths, which enables us to put 5 tenths in each group.

Once the 20 tenths are distributed, each group will have 2 tens, 1 one, and 5 tenths, so $86 \div 4 = 21.5$.

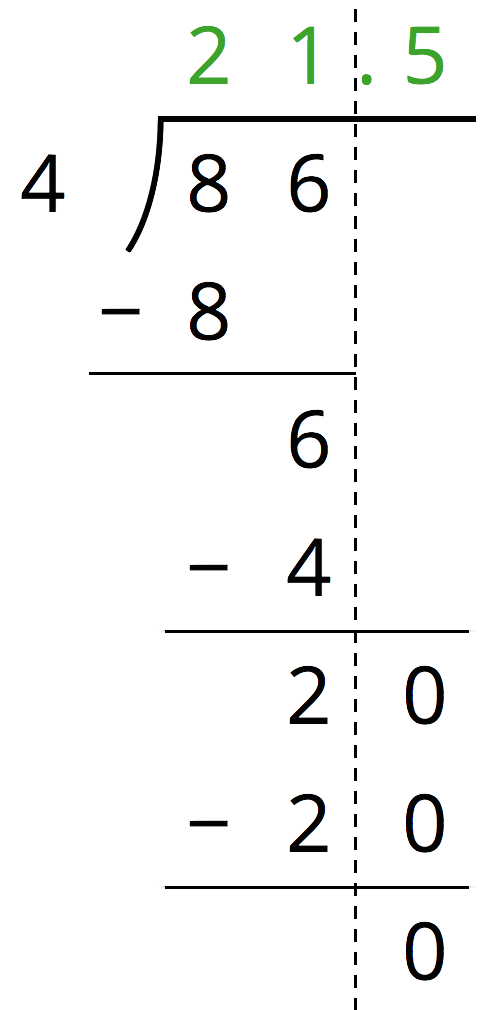
We can also calculate $86 \div 4$ using long division.

The calculation shows that, after removing 4 groups of 21, there are 2 ones remaining. We can continue dividing by writing a 0 to the right of the 2 and thinking of that remainder as 20 tenths, which can then be divided into 4 groups.

To show that the quotient we are working with now is in the tenth place, we put a decimal point to the right of the 1 (which is in the ones place) at the top. It may also be helpful to draw a vertical line to separate the ones and the tenths.

There are 4 groups of 5 tenths in 20 tenths, so we write 5 in the tenths place at the top. The calculation likewise shows $86 \div 4 = 21.5$.

Practice Problems ▶