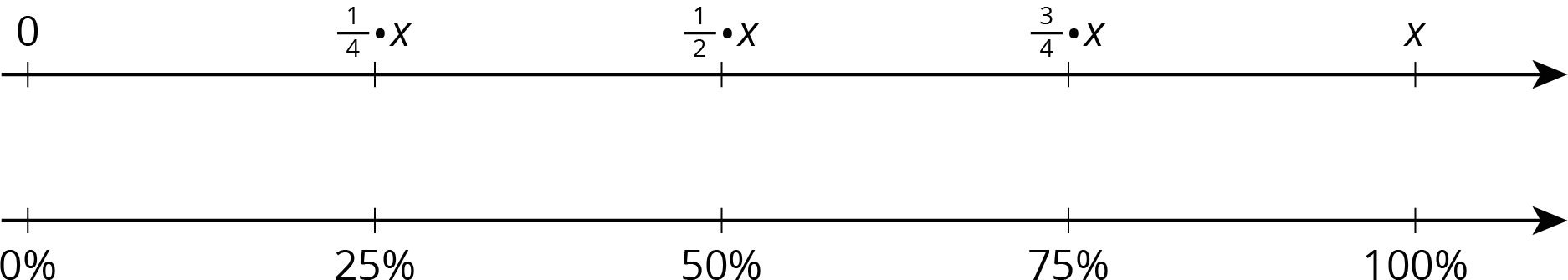13.1: What Percentage Is Shaded?
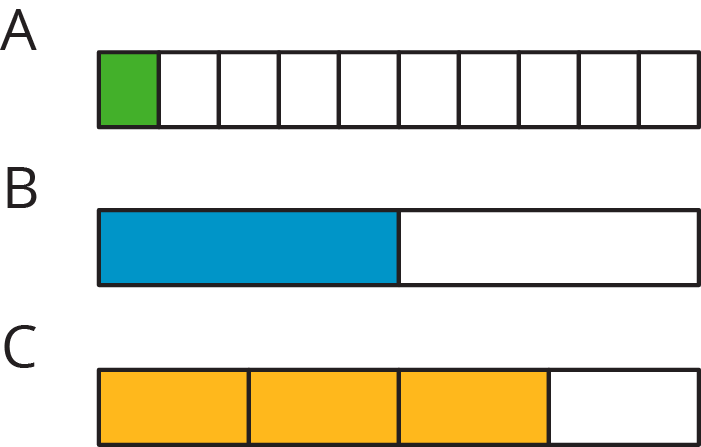
What percentage of each diagram is shaded?
Let’s contrast percentages and fractions.

What percentage of each diagram is shaded?
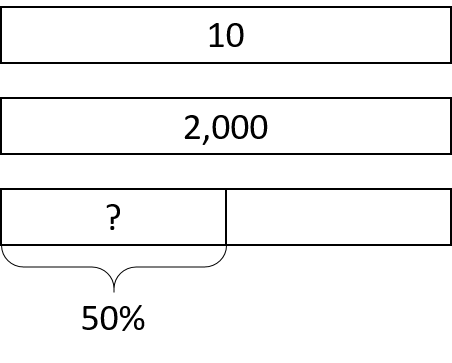
Explain how you can calculate each value mentally.
Match the percentage that describes the relationship between each pair of numbers. One percentage will be left over. Be prepared to explain your reasoning.
7 is what percentage of 14?
5 is what percentage of 20?
3 is what percentage of 30?
6 is what percentage of 8?
20 is what percentage of 5?
Certain percentages are easy to think about in terms of fractions.